平成１７年７月３日

[流れ星]

　　　　　第１５６回数学的な応募問題解答

　　　　　　＜解答募集期間：６月１１日〜７月３日

［放物線の長さ］

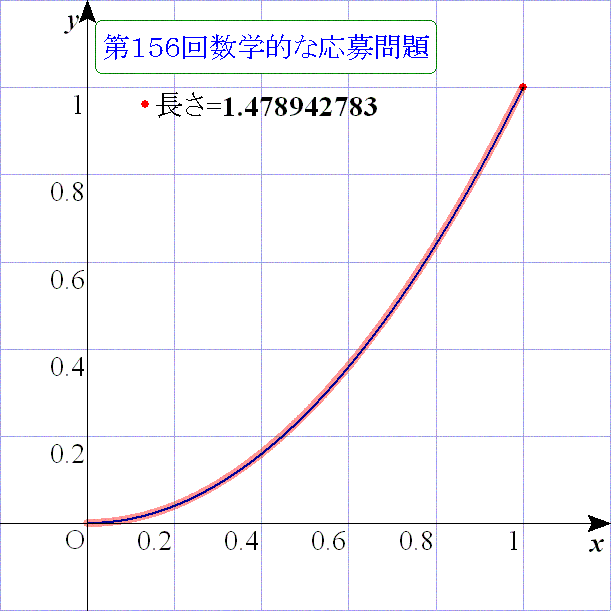
皆さん、今回は入試問題です。簡単に式がでてきますが・・・、

問題１：放物線　ｙ＝ｘ^２（０≦ｘ≦１）の長さを求めよ。

問題２：放物線　ｙ＝ｃｘ^２（ａ≦ｘ≦ｂ）の長さを求めよ。ただし、ａ、ｂ、ｃは定数です。

NO1「浜田明巳」6/11: 17時30分受信

「浜田明巳」6/16: 13時49分受信 更新7/3

問題１：曲線の長さの公式から，長さＬは，
　　Ｌ＝∫_{（０≦ｘ≦１）}{１＋(ｙ')^２}^１／２ｄｘ
　　　＝∫_{（０≦ｘ≦１）}{１＋(２ｘ)^２}^１／２ｄｘ
　ｘ＝ｔ／２とすると，ｄｘ／ｄｔ＝１／２
　ｘ＝０のときｔ＝０で，ｘ＝１のときｔ＝２
　∴Ｌ＝∫_{（０≦ｔ≦２）}(１＋ｔ^２)^１／２・１／２・ｄｔ
　　　＝１／２・∫_{（０≦ｔ≦２）}(１＋ｔ^２)^１／２ｄｔ
　　　＝１／２・∫_{（０≦ｔ≦２）}ｔ'(１＋ｔ^２)^１／２ｄｔ
　　　＝１／２・{［ｔ(１＋ｔ^２)^１／２］_{（０≦ｔ≦２）}−∫_{（０≦ｔ≦２）}ｔ・１／２・(１＋ｔ^２)^−１／２・２ｔｄｔ}
　　　＝５^１／２−１／２・∫_{（０≦ｔ≦２）}ｔ^２／(１＋ｔ^２)^１／２ｄｔ
　　　＝５^１／２−１／２・∫_{（０≦ｔ≦２）}{(１＋ｔ^２)−１}／(１＋ｔ^２)^１／２・ｄｔ
　　　＝５^１／２−１／２・∫_{（０≦ｔ≦２）}{(１＋ｔ^２)^１／２−１／(１＋ｔ^２)^１／２}ｄｔ
　　　＝５^１／２−Ｌ＋１／２・∫_{（０≦ｔ≦２）}１／(１＋ｔ^２)^１／２ｄｔ
　∴２Ｌ＝５^１／２＋１／２・∫_{（０≦ｔ≦２）}１／(１＋ｔ^２)^１／２・{ｔ＋(１＋ｔ^２)^１／２}／{ｔ＋(１＋ｔ^２)^１／２}・ｄｔ
　　　　＝５^１／２＋１／２・∫_{（０≦ｔ≦２）}{ｔ／(１＋ｔ^２)^１／２＋１}／{ｔ＋(１＋ｔ^２)^１／２}・ｄｔ
　　　　＝５^１／２＋１／２・∫_{（０≦ｔ≦２）}{ｔ＋(１＋ｔ^２)^１／２}'／{ｔ＋(１＋ｔ^２)^１／２}・ｄｔ
　　　　＝５^１／２＋１／２・［log{ｔ＋(１＋ｔ^２)^１／２}］_{（０≦ｔ≦２）}
　　　　＝５^１／２＋１／２・log(２＋５^１／２)
　∴Ｌ＝１／２・５^１／２＋１／４・log(２＋５^１／２)

問題２：問題１と同様に，
　　∫(１＋ｔ^２)^１／２ｄｔ＝１／２・ｔ(１＋ｔ^２)^１／２＋１／２・log{ｔ＋(１＋ｔ^２)^１／２}＋Ｃ
　　　＝１／２・[ｔ(１＋ｔ^２)^１／２＋log{ｔ＋(１＋ｔ^２)^１／２}]＋Ｃ（Ｃは積分定数）
となる．
　故に長さＬは，
　　Ｌ＝∫_{（ａ≦ｘ≦ｂ）}{１＋(ｙ')^２}^１／２ｄｘ
　　　＝∫_{（ａ≦ｘ≦ｂ）}{１＋(２ｃｘ)^２}^１／２ｄｘ
　ｘ＝ｔ／(２ｃ)とすると，ｄｘ／ｄｔ＝１／(２ｃ)
　ｘ＝ａのときｔ＝２ａｃで，ｘ＝ｂのときｔ＝２ｂｃ
　∴Ｌ＝∫_{（２ａｃ≦ｔ≦２ｂｃ）}(１＋ｔ^２)^１／２・１／(２ｃ)・ｄｔ
　　　＝１／(２ｃ)・∫_{（２ａｃ≦ｔ≦２ｂｃ）}(１＋ｔ^２)^１／２ｄｔ
　　　＝１／(２ｃ)・１／２・［ｔ(１＋ｔ^２)^１／２＋log{ｔ＋(１＋ｔ^２)^１／２}］_{（２ａｃ≦ｔ≦２ｂｃ）}
　　　＝１／(４ｃ)・（[２ｂｃ(１＋４ｂ^２ｃ^２)^１／２＋log{２ｂｃ＋(１＋４ｂ^２ｃ^２)^１／２}]−[２ａｃ(１＋４ａ^２ｃ^２)^１／２＋log{２ａｃ＋(１＋４ａ^２ｃ^２)^１／２}]）
　　　＝１／(４ｃ)・[２ｂｃ(１＋４ｂ^２ｃ^２)^１／２−２ａｃ(１＋４ａ^２ｃ^２)^１／２＋log{２ｂｃ＋(１＋４ｂ^２ｃ^２)^１／２}−log{２ａｃ＋(１＋４ａ^２ｃ^２)^１／２}]
　大変な計算でした．

（別解）問題１において，GRAPESでも解いてみた．
（スクリプト）（コピーする場合は，全角の空白を半角の空白にして下さい）
# //Clickで計算開始
# k:=.001
# d:=0
# u:=0
# for a:=0+k to 1+k*.5 step k
# 　d:=d+Sqrt((u-a)*(u-a)+(u*u-a*a)*(u*u-a*a))
# 　draw
# 　u:=a
# next a
# ---
　これにより長さは1.478942783となり，１／２・５^１／２＋１／４・log(２＋５^１／２)の近似値1.47894とほぼ等しい事が分かる．

NO2「中川幸一」6/12: 18時01分受信 更新7/3

「解答」です。

NO3「cbc」　　 6/12: 20時11分受信 更新7/3
＜「cbc」：今回は積分計算だけが狙い？絶対値の処理でミスを犯すとこでした＾＾＞

NO4「H7K」　　 6/12: 22時22分受信 更新7/3

NO5「Toru」 6/14: 16時32分受信 更新7/3

まず以前にも出た？
I=∫√(1+t^2) dt の形の積分を片付けておきます。
部分積分法によって
I=t√(1+t^2)-∫t^2/√(1+t^2)dt= t√(1+t^2)-I+∫1/√(1+t^2)dt
より　I= 1/2(t√(1+t^2)+∫1/√(1+t^2)dt)
J=∫1/√(1+t^2)dt  については　s=t+√(1+t^2)とおくと1/s= -t+√(1+t^2)
√(1+t^2) =(s+1/s)/2  t=(s-1/s)/2  dt/ds=(1+1/s^2)/2
からJ=∫(1+1/s^2)/(s+1/s) ds=∫ds/s=log｜s｜=log（t+√(1+t^2)）
これからI=1/2(t√(1+t^2)+ log（t+√(1+t^2))）

さてやっと本題
問題１　求める長さは
　　　∫[x=0〜1]√(1+(dy/dx)^2)dx =∫[x=0〜1]√ (1+4x^2)dx  (t=2xとして)
=1/2 ∫[t=0〜2]√ (1+t^2) dt=1/4 [t√(1+t^2)+ log(t+√(1+t^2))] [t=0〜2]
= (2√5+log(2+√5))/4

問題２　同様に
∫[x=a〜b]√(1+(dy/dx)^2)dx =∫[x=a〜b]√ (1+4c^2x^2)dx  (t=2cxとして)
=1/2c ∫[t=2ac〜2bc]√ (1+t^2) dt=1/4c [t√(1+t^2)+ log(t+√(1+t^2))] [t=2ac
〜2bc]= 1/2(b√(1+4b^2c^2)-a√(1+4a^2c^2))+1/4c log（(2bc+
√(1+4b^2c^2))/(2ac+√(1+4a^2c^2))）

　あまりきれいになりませんでした。「2次曲線の弧長は円と放物線とのほかは楕円積分に帰する」というところへつながるのですね。
ところでこれって本当に入試問題ですか？　　　

NO6「uchinyan」6/20　18時28分受信 <br>

NO6「uchinyan」6/22　11時16分受信 更新7/3<br>　
＜uchinyan：済みませんが、解答、少し追加しました。添付したもので置き換えてください。＞
＜水の流れ：他の解答者から　ｃ　の正負の場合分けのがあり、そうだったのか　と　考えています。＞
＜uchinyan：あ、これは確かにそうなのですが、結局、同じ式になることは確認済みです。したがって、場合分けは不要だと思います。＞
＜uchinyan：出題の意図がイマイチ分からなかったので、どうしようか迷ったのですが、一応。＞

問題1
y = x^2, dy/dx = 2x より、求める曲線の長さ L は、
L = ∫[0,1] sqrt(1 + (dy/dx)^2) dx = ∫[0,1] sqrt(1 + 4 * x^2) dx
2x -> x と変数変換して
L = 1/2 * ∫[0,2] sqrt(1 + x^2) dx
ここで、
{1/2 * (x * sqrt(1 + x^2) + log(x + sqrt(1 + x^2)))}' = sqrt(1 + x^2)
なので、
L = 1/2 * [1/2 * (x * sqrt(1 + x^2) + log(x + sqrt(1 + x^2)))][0,2]
= 1/4 * (2 * sqrt(5) + log(2 + sqrt(5))
これで、いいのでしょうか。

問題2
基本的には、同じですが、若干場合分けをして確認です。
y = cx^2, dy/dx = 2cx より、求める曲線の長さ L は、
L = ∫[a,b] sqrt(1 + (dy/dx)^2) dx = ∫[a,b] sqrt(1 + 4c^2 * x^2) dx
c not= 0 のとき：(c > 0 でも c < 0 でも、同じ式になります。)
2cx -> x と変数変換して
L = 1/2c * ∫[2ac,2bc] sqrt(1 + x^2) dx
= 1/2c * [1/2 * (x * sqrt(1 + x^2) + log(x + sqrt(1 + x^2)))][2ac,2bc]
= 1/4c * {(2bc * sqrt(1 + (2bc)^2) + log(2bc + sqrt(1 + (2bc)^2))
　- (2ac * sqrt(1 + (2ac)^2) + log(2ac + sqrt(1 + (2ac)^2)))}
= 1/4c * {2bc * sqrt(1 + (2bc)^2) - 2ac * sqrt(1 + (2ac)^2)
　+ log((2bc + sqrt(1 + (2bc)^2))/(2ac + sqrt(1 + (2ac)^2)))}
c = 0 のとき：
L = ∫[a,b] sqrt(1) dx = b-a
なお、c not= 0 で c -> 0 とすると、b-a になります。考察2を参照。

考察1：
∫sqrt(1 + x^2) dx の積分は、よく知られているのでいちいち計算しませんでし
たが、ひょっとしたら、
この計算をするのが、この問題の意図だったのかもしれません。
一応、方針だけを書いてきます。
(方針1)
∫sqrt(1 + x^2) dx = x * sqrt(1 + x^2) - ∫sqrt(1 + x^2) dx + ∫1/sqrt(1 +
x^2) dx
∫sqrt(1 + x^2) dx = 1/2 * {x * sqrt(1 + x^2) + ∫1/sqrt(1 + x^2) dx}
なので、∫1/sqrt(1 + x^2) dx を求めればOKです。
これは、t = x + sqrt(1 + x^2) とおくと、dt/dx = t/sqrt(1 + x^2) となるの
で、これからすぐにもとまります。
(方針2)
t = x + sqrt(1 + x^2) とおいて、変形すると、x = (t^2 - 1)/2t, dt/dx =
t/sqrt(1 + x^2) となるので、
これから、∫sqrt(1 + x^2) dx は、t の有理式になり、積分可能です。
注：
t = x + sqrt(1 + x^2) の変換は、y^2 = x^2 + 1 の双曲線の漸近線 y = -x に
平行な直線で y > 0 の枝を
一意に切っていることに対応します。よくある、有理化の手法ですね。
(方針3)
いわゆる双曲線関数を使って、x = sinh(t) = 1/2 * (exp(t) - exp(-t)) とお
きます。
cosh(t) = 1/2 * (exp(t) + exp(-t)), cosh^2(t) - sinh^2(t) = 1,
sqrt(1 + x^2) = cosh(t), dx/dt = cosh(t), cosh^2(t) = 1/2 * (1 + cosh(2t)),
(sinh(t))' = cosh(t) などから計算ができます。
(以下少し追加です。)
(方針4)
tx + 1 = sqrt(1 + x^2) とおいても、計算できます。
x = 2t/(1 - t^2) = - {1/(t+1) + 1/(t-1)}
dx/dt = 1/(t+1)^2 + 1/(t-1)^2
sqrt(1 + x^2) = tx + 1 = - t/(t+1) - t/(t-1) + 1
などを使うと、やはり、有理式の積分になって計算可能です。
この方針は、(方針2)と同様で、双曲線と直線の交点を用いる方法です。
ただし、計算は少し大変です。
(方針5)
x = tanθとおく方法もあります。-π/2 < θ < π/2 なので、cosθ > 0 で、
dx/dθ = 1/(cosθ)^2
sqrt(1 + x^2) = sqrt(1 + (tanθ)^2) = sqrt(1/(cosθ)^2) = 1/cosθ
これらから三角関数の積分になり、この三角関数の積分は、t = sinθ として、
やはり有理式の積分に変換できます。

考察2：
問題2で、c not= 0 のときの式、
L = 1/4c * {2bc * sqrt(1 + (2bc)^2) - 2ac * sqrt(1 + (2ac)^2)
　+ log((2bc + sqrt(1 + (2bc)^2))/(2ac + sqrt(1 + (2ac)^2)))}
で、c -> 0 とすると、
(Lの第1項) -> 1/2 * (b-a)
(Lの第2項)
= 1/4c * {log(2bc + sqrt(1 + (2bc)^2)) - log(2ac + sqrt(1 + (2ac)^2))}
= 1/4c * {log(1 + 2bc + 1/2 * (2bc)^2 + o(c^2)) - log(1 + 2ac + 1/2 *
(2ac)^2 + o(c^2))}
= 1/4c * {1 - (-2bc) + o(c^2) - (1 - (-2ac) + o(c^2))}
= 1/4c * {2bc - 2ac + o(c^2)}
-> 1/2 * (b-a)
結局、c -> で L -> b-a となり、c = 0 の場合に一致します。
ただ、これを、マクローリン展開なしで示すのは、少し大変そうです。
ひょっとして、これが出題の意図だったのでしょうか。
(以下少し追加です。)
高校で平均値の定理って習うんでしたか？
もしそうならば、a not= b の場合(a = b の場合は、明らかに 0 です。)、
f(x) = log(x + sqrt(1 + x^2)) とおいて、f'(x) = 1/sqrt(1 + x^2) で、
c not= 0 のとき、
(f(2bc) - f(2ac))/(2bc - 2ac) = f'(d), 2ac < d < 2bc
(Lの第2項)
= 1/4c * {log(2bc + sqrt(1 + (2bc)^2)) - log(2ac + sqrt(1 + (2ac)^2))}
= 1/4 * 2(b-a) * (f(2bc) - f(2ac))/(2bc - 2ac)
= 1/4 * 2(b-a) * f'(d)
c -> 0 で d -> 0 となり、f'(d) -> 1 なので、
(Lの第2項) -> 1/2 * (b-a)
とすれば、いいですね ^^;

NO7「kashiwagi」6/21 20時22分受信 更新7/3　
この様な問題 が入試にでるのですか・・・。私は大学の教養課程でこの公式を知ったのですが、 現在は高校で教えるのですね。うーん。

＜水の流れ：過去に慶応大学の入試の中でありましたし、この積分は公式とは言わないまでも、計算過程を記憶しておくと助かります。＞

156回解答

　以下の公式を使用します。

ですから

問１．であるからA＝1/4

　　　　因って、　が求めるものである。

問２． 問１と同様にする。但し、ｃの正負で場合訳をする。

�@ｃ≧0の時

　　　-

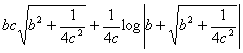�Aｃ＜0の時

　　　＋

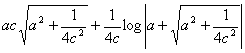
NO8「kasama」　6/27 16時05分受信 更新7/3　
　

さて、今回の問題です。『簡単に式がでてきますが・・・』とコメントがありました。添付リストの通り、あまり苦労せずに積分できますが、これでよろしいのでしょうか。
興味本位にMathmaticsにやらせてみました。三角関数の逆関数や双曲線正弦などが出てきて、まぁあっているのでしょうけど、人間味のある式(笑)ではなかったので、
素手でコツコツやりました。

【問題２】
関数y=f(x)の点a、b間の長さsは
　s=∫√(1+(dy/dx)²)dx　(a≦x≦b)
です。ここで、f(x)=cx²とすると、
　s=∫√(1+(2cx)²)dx　(a≦x≦b)
ですが、公式∫√(x²+α)dx=[x√(x²+α)+αlog{x+√(x²+α)}]/2+C(=定数)を利用すると、
　s=2c∫√(x²+1/2c²)dx 　(a≦x≦b)
　 ={b√(1+(2bc)²)-a√(1+(2ac)²)}/2 + [log{√(1+(2bc)²)+2bc}+log{√(1+(2ac)²)-2ac}]/(4c)
です。
【問題１】
上式にa=0、b=1、c=1を代入して、整理すると、
　s={log(2+√5)+2√5}/4
となります