平成１７年９月４日

[流れ星]

　　　　　第１５９回数学的な応募問題解答

　　　　　　＜解答募集期間：８月１３日〜９月４日

［綺麗な不等式］

皆さん、今回の問題です。考えてください。

　　　

NO1「H7K」 8/13　17時59分受信 更新9/4

　まず，次が成り立っていることを確認．
定理A: [0,∞)でf''>0のとき，正数a_1, a_2,..., a_nについて，f((a_1+...+a_n)/n) <= ( f(a_1)+f(a_2)+...+f(a_n) )/n.

補題1 a+b=1, p, q>0, f''は[0,∞)で>0ならば，f(ap+bq)<=af(p)+bf(q)．等号はp=qのみ．
とりあえず，ここではこれを「凸関数の性質より明らか」と認めます．Taylor展開は使わないことにしよう．

すると，定理Aが，以下のように示せる．
f(a_1)+f(a_2)+...+f(a_n) = 2(f(a_1)/2+f(a_2)/2)+f(a_3)+f_(a_4)+...+f(a_n)
 >= 2f( (a_1+a_2)/2 ) + f(a_3)+f_(a_4)+...+f(a_n)
   = 3( 2f( (a_1+a_2)/2 )/3 + f(a_3)/3 )+f_(a_4)+...+f(a_n)
 >= 3f( (a_1+a_2+a_3)/3 ) + f_(a_4)+...+f(a_n)
 >= ..... >=nf((a_1+...+a_n)/n).

等号成立条件は，全ての不等号が等号となるとき，つまり，a_1=a_2=...=a_nのとき．
さて，以下，x>0とする．

f(x)=(x+1/x)^2とすると，f''=4(x+1/x)/x^3+2(1-1/x^2)^2>0だから，
定理Aが成立する．
問題1. (f(a)+f(b))/2 >= f((a+b)/2)=(1/2+2)^2=25/4．両辺を2で掛ければ題意を得る．
問題2. 同様に，f(a)+f(b)+f(c) >= 3 f(1/3) = 3*100/9 = 100/3.
問題3, 4
(左辺)>= n f(1/n) = (n^2+1)^2/n. (問題3はn=4の場合だから，289/4.)である．
これが最大であることは，a_1=a_2=...=a_n=1/nのときに，左辺がこの値と等しくなることからわかる．

NO2「uchinyan」8/16　17時48分受信 更新9/4

第１５９回数学的な応募問題の解答　まず、次の補題を証明しておきます。
補題：
y = f(x) が二回微分可能で f''(x) >= 0 とする。
n >= 2 で p1 + p2 + ... + pn = 1, p1, p2, ..., pn > 0 のとき、
f(p1 * x1 + p2 * x2 + ... + pn * xn)
　<= p1 * f(x1) + p2 * f(x2) + ... + pn * f(xn)
(証明)
* n = 2 の場合
対称性より、x1 <= x2 として一般性を失わない。
x1 = x2 のときは明らか。なお、この場合に等号が成立。
x1 < x2 のとき。
p1 ＋ p2 = 1 なので、
x2 - (p1 * x1 + p2 * x2) = p1 * (x2 - x1) > 0
(p1 * x1 + p2 * x2) - x1 = p2 * (x2 - x1) > 0
より、
x1 < p1 * x1 + p2 * x2 < x2
そこで、平均値の定理より、
(f(p1 * x1 + p2 * x2) - f(x1))/((p1 * x1 + p2 * x2) - x1) = f'(c1)
x1 < c1 < p1 * x1 + p2 * x2
(f(x2) - f(p1 * x1 + p2 * x2))/(x2 - (p1 * x1 + p2 * x2)) = f'(c2)
p1 * x1 + p2 * x2 < c2 < x2
ここで、f''(x) >= 0 より、f(x) は単調増加で、f'(c1) <= f'(c2)
等号は、c1, c2 の間で、常に、f''(x) = 0 の場合。
このとき、p1 ＋ p2 = 1 に注意して変形すると、
(f(p1 * x1 + p2 * x2) - f(x1))/((p1 * x1 + p2 * x2) - x1)
　<= (f(x2) - f(p1 * x1 + p2 * x2))/(x2 - (p1 * x1 + p2 * x2))
(f(p1 * x1 + p2 * x2) - f(x1))/(p2 * (x2 - x1))
　<= (f(x2) - f(p1 * x1 + p2 * x2))/(p1 * (x1 - x2))
p1 * (f(p1 * x1 + p2 * x2) - f(x1))
　<= p2 * (f(x2) - f(p1 * x1 + p2 * x2))
f(p1 * x1 + p2 * x2) <= p1 * f(x1) + p2 * f(x2)
で成立する。　ただし等号は、
x1 = x2　又は　f''(x) = 0 がいえる範囲で恒等的に成立する　場合
後者は、f(x) に依存するので、一般には確定できない。
常に f''(x) > 0 の場合は、等号は、x1 = x2 の場合に限る。
* n の場合
2, ..., n-1 で成立したとする。
すると、q = p1 + p2 + ... + p_(n-1) とおくと、q > 0 で、q + pn = 1
そこで、
f(p1 * x1 + p2 * x2 + ... + pn * xn)
= f((p1 * x1 + p2 * x2 + ... + p_(n-1) * x_(n-1))/q * q + pn * xn)
<= q * f((p1 * x1 + p2 * x2 + ... + p_(n-1) * x_(n-1))/q) + pn * f(xn)
= q * f(p1/q * x1 + p2/q * x2 + ... + p_(n-1)/q * x_(n-1)) + pn * f(xn)
p1/q + p2/q + ... + p_(n-1)/q = 1 より、
<= q * (p1/q * f(x1) + p2/q * f(x2) + ... + p_(n-1)/q * f(x_(n-1)))
　+ pn * f(xn)
= p1 * f(x1) + p2 * f(x2) + ... + pn * f(xn)
で成立。
等号は、常に f''(x) > 0 ならば、x1 = x2 = ... = xn に限る。
f''(x) = 0 がある場合には、一般に f(x) に依存する。
(証明終)
今回の問題では、f''(x) > 0 の場合だけを使います。
(補足)
例えば、f(x) = ax + b, a, b は 0 でも可、の場合、常に f''(x) = 0 で、
f(x) の不等式は常に等式になります。まぁ、線形の関係なので当たり前ですね。
　さて、本題です。すべて同様なので、問題4：から解きます。　なお、コーシー・シュワルツの不等式は、使用しませんでした。
問題4：
まず、補題で p1 = p2 = ... = pn = 1/n とおくと、
1/n * (f(x1) + f(x2) + ... + f(xn)) >= f((x1 + x2 + ... + xn)/n)
になります。以下、これを使います。
ここで、f(x) = (x + 1/x)^2 = x^2 + 2 + 1/x^2 とおくと、
f''(x) = 2 + 6/x^4 > 0
なので、
1/n * ((x1 + 1/x1)^2 + (x2 + 1/x2)^2 + ... + (xn + 1/xn)^2)
　>= ((x1 + x2 + ... + xn)/n + n/(x1 + x2 + ... + xn))^2
(x1 + 1/x1)^2 + (x2 + 1/x2)^2 + ... + (xn + 1/xn)^2
　>= n * ((x1 + x2 + ... + xn)/n + n/(x1 + x2 + ... + xn))^2
x1 = a1, x2 = a2, ..., xn = an,  a1, a2, ..., an > 0 とすると、
(a1 + 1/a1)^2 + (a2 + 1/a2)^2 + ... + (an + 1/an)^2
　>= n * ((a1 + a2 + ... + an)/n + n/(a1 + a2 + ... + an))^2
a1 + a2 + ... + an = 1 なので、
(a1 + 1/a1)^2 + (a2 + 1/a2)^2 + ... + (an + 1/an)^2
　>= n * (1/n + n)^2 = 1/n * (n^2 + 1)^2
ただし、等号は、a1 = a2 = ... = an = 1/n の場合です。
そこで、N = 1/n * (n^2 + 1)^2 になります。
問題1：
n = 2 の場合で、N = 1/2 * (2^2 + 1)^2 = 25/2 なので、成立。
問題2：
n = 3 の場合で、N = 1/3 * (3^2 + 1)^2 = 100/3 なので、成立。
問題3：
n = 4 の場合で、N = 1/4 * (4^2 + 1)^2 = 289/4 となります。
(感想)
問題4：で、a1 + a2 + ... + an = 1 の条件で偏微分したときの値が0 となるのが、a1 = a2 = ... = an = 1/n なのはすぐに分かるので、
左辺は完全平方の和であることから、直感的には、このときに、
左辺は最小値になるだろう、と思われます。実際、これが、N = 1/n * (n^2 + 1)^2 になるわけですね。
(蛇足)
コーシー・シュワルツの不等式は使用しませんでしたが、先ほどの補題で、
f(x) = x^2, (y1)^2 + (y2)^2 + ... + (yn)^2 = y,
p1 = (y1)^2/y, p2 = (y2)^2/y, ..., pn = (yn)^2/y
とおくと、f''(x) = 2 > 0 で、
p1 * (x1)^2 + p2 * (x2)^2 + ... + pn * (xn)^2
　>= (p1 * x1 + p2 * x2 + ... + pn * xn)^2
がいえ、
(y1)^2/y * (x1/y1)^2 + (y2)^2/y * (x2/y2)^2 + ... + (yn)^2/y * (xn/yn)^2
　>= ((y1)^2/y * x1/y1 + (y2)^2/y * x2/y2 + ... + (yn)^2/y * xn/yn)^2
1/y * ((x1)^2 + (x2)^2 + ... + (xn)^2)
　>= 1/y^2 * (x1 * y1 + x2 * y2 + ... + xn * yn)^2
((x1)^2 + (x2)^2 + ... + (xn)^2) * y
　>= (x1 * y1 + x2 * y2 + ... + xn * yn)^2
((x1)^2 + (x2)^2 + ... + (xn)^2) * ((y1)^2 + (y2)^2 + ... + (yn)^2)
　>= (x1 * y1 + x2 * y2 + ... + xn * yn)^2
ただし、等号は、x1/y1 = x2/y2 = ... = xn/yn となって、　コーシー・シュワルツの不等式が証明できます。

NO3「Toru」　　8/18 14時52分受信 更新9/4

第１５９回解答を送ります。直観的なものと、少しだけ理論的なものを書いてみました。いろいろ考えると不満の残るところがあり、今一つですが、余り時間も書けられず、この当たりで手を打っておきます。
　
　y=f(x)が凸関数の時（f'(x)≡0はのぞいて）
この曲線上の点A1(a1,f(a1)),A2(a2,f(a2)),-----,An(an,f(an)) (a1≦a2≦---≦an)
とすると、凸型N角形A1A2---Anは曲線の上側に位置し、
点((a1+a2+----+an)/n,(f(a1)+f(a2)+-----+f(an))/n)は凸型N角形A1,A2,----,Anの
重心であるから、明らかに曲線より上に位置する。よって
f（(a1+a2+----+an)/n）≦(f(a1)+f(a2)+-----+f(an))/n　等号はa1=a2=----=anの時、

　あるいは、もう少し厳密に、
ある区間内でf’’(x)≧0、この区間内にa1≦a2≦-----≦an　をとったとして
n f((a1+a2+----+an)/n)≦(f(a1)+f(a2)+-----+f(an))を数学的帰納法で証明する。
n=1の時は明らかに成り立つ n=kで成り立つとして
bk=(a1+a2+----+ak)/kとすると、kf(bk) ≦f(a1)+f(a2)+---+f(ak)　でまたa1≦a2
≦-----≦a(k+1)よりbk≦a(k+1),
bk<a(k+1)の時、bk+1は区間(bk,a(k+1))を１：kに内分する点で、（bk,b(k+1)）
(b(k+1),a(k+1))に平均値の定理を適用すれば、
 (f(b(k+1))-f(bk))/(b(k+1)-bk)=f’(ck1),
(f(a(k+1))-f(b(k+1))/(a(k+1)-b(k+1))=f’(ck2)
bk<ck1<b(k+1)<ck2<a(k+1)となるck1,ck2が存在する。f’’(x)≧0 の時　f’(x)は
単調増加であるから、f’(ck1)≦f’(ck2) より
(f(b(k+1))-f(bk))/(b(k+1)-bk)≦(f(a(k+1))-f(b(k+1))/(a(k+1)-b(k+1))　
k(b(k+1)-bk)= a(k+1)-b(k+1)とから
(k+1)f(b(k+1))≦(kf(bk)+f(a(k+1)))≦f(a1)+f(a2)+-----+f(a(k+1))
　bk=a(k+1)の時a1=a2=-----=ak=a(k+1)
で(k+1)f(b(k+1))=f(a1)+f(a2)+-----+f(a(k+1))
といずれの場合も　n=k+1で成りたつ。
　よって数学的帰納法より、nf((a1+a2+----+an)/n)≦f(a1)+f(a2)+-----+f(an)は証明された。
（等号はa1=a2=----=an, or　点(ak,f(ak))  (k=1,2,----,n)が一直線上にある時）

f(x)=(x+1/x)^2 とするとf’(x)=2(x+1/x)(1-1/x^2)=2(x-1/x^3), f’’
(x)=2(1+3/x^4)>0　　よってこれに上記を適用する、
1) f(a)+f(b)≧2f((a+b)/2)=2f(1/2)=25/2 等号はa=b=1/2の時
2) f(a)+f(b)+f(c)≧3((a+b+c)/3)=3f(1/3)=100/3 等号はa=b=c=1/3の時
3) f(a)+f(b)+f(c)+f(d)≧4((a+b+c+d)/4)=4f(1/4)=289/4 等号はa=b=c=d=1/4
4) f(a1)+f(a2)+---+f(an≧n((a1+a2+----+an)/n)=nf(1/n)=((n^2+1)^2)／n

NO4「ice」　　 8/18 22時55分受信 更新9/4

NO5「kashiwagi」8/21 12時05分受信 更新9/4

　159回解答

問1.まずコーシー・シュワルツの不等式で証明する。

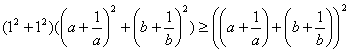　　　が成り立ち、等号はと各々が正の数との条件から　で成立する。

ところで相加平均、相乗平均及び調和平均の関係から

　が成り立ち、

よりである。

この関係をコーシー・シュワルツの不等式に代入し、

＝

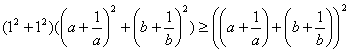　が成立する。

次に凸関数の性質から証明する。

今、関数　　を考えると、その二次導関数は　　であるから　　が成り立つ。　

即ち、

これらより　となる。

問2.　問1と全く同様にコーシー・シュワルツの不等式で3数の計算を行うと証明でき、等号は　で成立する。

　　　又、凸関数の性質　からも同様に証明される。

問3.　4数の調和平均の関係を使うと

　　　　となる。

　　　因って求める値　　となる。

問4.　問1〜3の結果から

　　　　 の時　

　　　　　　の時　

　　　　の時　　　であるから

　の時　　となるものと推定される。

NO6「cbc」　　 8/22 10時31分受信 更新9/4

NO7「kasama」 8/23 09時32分受信 更新9/4

さて、今回は不等式に関する出題ですね。
やり方は幾通りかあろうかと思いますが、まず{f(x)+f(y)}/2≧f((x+y)/2)を一般化して、相加平均≧調和平均を利用する方法で取り組みました。
まぁ、(x+1/x)^2は下に凸の関数ですから、直感的に(a1+1/a1)^2+(a2+1/a2)^2+・・・+(an+1/an)^2も下に凸で極値が存在するとすれば、最小値と考えられるので、Lagrangeの乗数法でやるのが手取り早いかもしれません。

まず、一般化から始めます。問題文に書いてある定理より、f''(x)>0のとき、{f(x)+f(y)}/2≧f((x+y)/2)ですが、これを少し拡張しまして、
　{f(x₁)+f(x₂)+･･･+f(x_n)}/n≧f((x₁+x₂+･･･+x_n)/n) ･･･(1)
とやります(補足参照)。そして、n≧2に対して、二次関数f(x)=nx²とすると、f''(x)=2n>0です。また、正の実数でa₁+a₂+･･･+a_n=1を満たすようなa₁、a₂、･･･、a_nに対して、x₁=a₁+1/a₁、x₂=a₂+1/a₂、･･･、x_n=a_n+1/a_nとすると、(1)式の左辺は
　左辺={n(a₁+1/a₁)²+n(a₂+1/a₂)²+･･･+n(a_n+1/a_n)²}/n=(a₁+1/a₁)²+(a₂+1/a₂)²+･･･+(a_n+1/a_n)² ･･･(2)
一方、(1)式の右辺は、
　右辺=n{(a₁+1/a₁+a₂+1/a₂+･･･+a_n+1/a_n)/n}²=(1+1/a₁+1/a₂+･･･+1/a_n)²/n ･･･(3)
です。ここで、受験数学のテクニックの一つとしてよく知られている『相加平均≧調和平均』を利用して、
　(a₁+a₂+･･･+a_n)/n≧n/(1/a₁+1/a₂+･･･+1/a_n)⇒1/a₁+1/a₂+･･･+1/a_n≧n²/(a₁+a₂ +･･･+a_n)⇒1/a₁+1/a₂+･･･+1/a_n≧n²
これを(3)に適用すると、
　(1+1/a₁+1/a₂+･･･+1/a_n)²/n≧(1+n²)²/n
ですから、
　(a₁+1/a₁)²+(a₂+1/a₂)²+･･･+(a_n+1/a_n)²≧(1+n²)²/n ･･･(4)
となります。

上記の考察を基にして問題を考えます。
【問題１、２、３】　n=2,3,4に特化したケースです。
【問題４】　(4)式より、N=(1+n²)²/nです。

【補足】
ξ=(x₁+x₂+･･･+x_n)/nとして、f(x_i)をξの近傍にTaylor展開すると、
　f(x_i)=f(ξ)+(x_i-ξ)f'(ξ)+(x_i-ξ)²f''(ξ+θ_i(x_i-ξ))/2, 0<θ_i<1　(i=1,2,･･･,n)
ですが、f''(x)>0なので、
　f(x_i)≧f(ξ)+(x_i-ξ)f'(ξ)　(i=1,2,･･･,n)
となり、i=1,2,･･･,nで和をとって、
　f(x₁)+f(x₂)+･･･+f(x_n)≧nf(ξ)+(x₁+x₂+･･･+x_n-ξ)f'(ξ)=nf(ξ)⇒{f(x₁)+f(x₂)+･･･+f(x_n)}/n≧f((x₁+x₂+･･･+x_n)/n)　　です。

NO8「浜田明巳」8/31 14時24分受信 更新9/4

　第１５９回数学的な応募問題解答
　いつものようにエクセルのマクロで求めた．数学的には正しくない方法である．
　０＜ａi≦ａj＜１（ｉ＜ｊ）としてａi（ｉ＝１，２，………，ｎ）を設定して，シラミつぶしで
　　ｐ＝(ａ1＋１／ａ1)^2＋(ａ2＋１／ａ2)^2＋………＋(ａn＋１／ａn)^2
を計算し，その最小値Ｎとそのときのａ1〜ａnを表示するようにしている．
　ただし闇雲にシラミつぶしの計算をしても，時間がかかるので，次のようにａiの範囲を限定する．
　０＜ａ1≦ａ2≦………≦ａn，ａ1＋ａ2＋………＋ａn＝１なので，
　　１＝ａ1＋ａ2＋………＋ａn≧ａ1＋ａ1＋………＋ａ1＝ｎａ1
　　∴０＜ａ1≦１／ｎ
　同様に，ａ1≦ａ2≦………≦ａn，ａ2＋ａ3＋………＋ａn＝１−ａ1なので，
　　１−ａ1＝ａ2＋ａ3＋………＋ａn≧ａ2＋ａ2＋………＋ａ2＝(ｎ−１)ａ2
　　∴ａ1≦ａ2≦(１−ａ1)／(ｎ−１)
　同様に，
　　ａ2≦ａ3≦(１−ａ1−ａ2)／(ｎ−２)
　　ａ3≦ａ4≦(１−ａ1−ａ2−ａ3)／(ｎ−３)
　　　………
となる．
　このマクロにより，ａ1＝ａ2＝………＝ａnのとき，最小になる事が分かるので，
　　ａ1＝ａ2＝………＝ａn＝１／ｎ
となり，最小値Ｎは
　　Ｎ＝ｎ{１／ｎ＋１／(１／ｎ)}^2＝ｎ(１／ｎ＋ｎ)^2＝(ｎ^2＋１)^2／ｎ
となる．
問題１．（ｎ＝２の場合）
問題２．（ｎ＝３の場合）
問題３．ｎ＝４の場合なので，Ｎ＝(４^2＋１)^2／４＝２８９／４
問題４．(ｎ^2＋１)^2／ｎ

（プログラム）（コピーする際は，全角の空白を縮小の空白に置き直して下さい）
Option Explicit
Sub Macro1()
　　Sheets("Sheet1").Select
　　Call m1
　　Call m2
　　Call m3
　　Call m4
End Sub
Sub m1() 'a
　　Dim n As Integer
　　Dim a As Double
　　Dim p As Double
　　n = 1
　　Cells(n, 1).Value = n
　　Range("B" & n).Select
　　a = 1
　　p = (a + 1 / a) * (a + 1 / a)
　　Cells(n, 3).Value = a
　　Cells(n, 2).Value = p
End Sub
Sub m2() 'a<=b
　　Dim n As Integer
　　Dim a As Double
　　Dim b As Double
　　Dim a_max As Double
　　Dim a_min As Double
　　Dim a_max0 As Double
　　Dim a_min0 As Double
　　Dim aa As Double
　　Dim p As Double
　　Dim min As Double
　　Dim kizami As Double
　　Dim dankai As Integer
　　n = 2
　　Cells(n, 1).Value = n
　　Range("B" & n).Select
　　min = 1000000
　　kizami = 0.01
　　a_min0 = kizami
　　a_max0 = 1 / n
　　For dankai = 1 To 14
　　　If dankai = 1 Then
　　　　a_min = a_min0
　　　　a_max = a_max0
　　　Else
　　　　a_min = Application.Max(aa - kizami, a_min0)
　　　　a_max = Application.min(aa + kizami, a_max0)
　　　　kizami = kizami * 0.1
　　　End If
　　　For a = a_min To a_max Step kizami
　　　　b = 1 - a
　　　　If a <= b And b < 1 Then
　　　　　p = (a + 1 / a) * (a + 1 / a) + (b + 1 / b) * (b + 1 / b)
　　　　　If min > p Then
　　　　　　min = p
　　　　　　aa = a
　　　　　　Cells(n, 2).Value = min
　　　　　　Cells(n, 3).Value = aa
　　　　　　Cells(n, 4).Value = b
　　　　　End If
　　　　End If
　　　Next a
　　Next dankai
End Sub
Sub m3() 'a<=b<=c
　　Dim n As Integer
　　Dim a As Double
　　Dim b As Double
　　Dim c As Double
　　Dim a_max As Double
　　Dim a_min As Double
　　Dim b_max As Double
　　Dim b_min As Double
　　Dim a_max0 As Double
　　Dim a_min0 As Double
　　Dim aa As Double
　　Dim bb As Double
　　Dim p As Double
　　Dim min As Double
　　Dim kizami As Double
　　Dim dankai As Integer
　　n = 3
　　Cells(n, 1).Value = n
　　Range("B" & n).Select
　　min = 1000000
　　kizami = 0.01
　　a_min0 = kizami
　　a_max0 = 1 / n
　　For dankai = 1 To 14
　　　If dankai = 1 Then
　　　　a_min = a_min0
　　　　a_max = a_max0
　　　Else
　　　　a_min = Application.Max(aa - kizami, a_min0)
　　　　a_max = Application.min(aa + kizami, a_max0)
　　　　kizami = kizami * 0.1
　　　End If
　　　　For a = a_min To a_max Step kizami
　　　　b_min = Application.Max(bb - kizami * 10, a)
　　　　b_max = Application.min(bb + kizami * 10, (1 - a) / 2)
　　　　For b = b_min To b_max Step kizami
　　　　　c = 1 - a - b
　　　　　If b <= c And c < 1 Then
　　　　　　p = (a + 1 / a) * (a + 1 / a) + (b + 1 / b) * (b + 1 / b) + (c + 1 / c) * (c + 1 / c)
　　　　　　If min > p Then
　　　　　　　min = p
　　　　　　　aa = a
　　　　　　　bb = b
　　　　　　　Cells(n, 2).Value = min
　　　　　　　Cells(n, 3).Value = aa
　　　　　　　Cells(n, 4).Value = bb
　　　　　　　Cells(n, 5).Value = c
　　　　　　End If
　　　　　End If
　　　　Next b
　　　Next a
　　Next dankai
End Sub
Sub m4() 'a<=b<=c<=d
　　Dim a As Double
　　Dim b As Double
　　Dim c As Double
　　Dim d As Double
　　Dim a_max As Double
　　Dim a_min As Double
　　Dim b_max As Double
　　Dim b_min As Double
　　Dim c_max As Double
　　Dim c_min As Double
　　Dim a_max0 As Double
　　Dim a_min0 As Double
　　Dim aa As Double
　　Dim bb As Double
　　Dim cc As Double
　　Dim p As Double
　　Dim min As Double
　　Dim kizami As Double
　　Dim dankai As Integer
　　n = 4
　　Cells(n, 1).Value = n
　　Range("B" & n).Select
　　min = 1000000
　　kizami = 0.01
　　a_min0 = kizami
　　a_max0 = 1 / n
　　For dankai = 1 To 14
　　　If dankai = 1 Then
　　　　a_min = a_min0
　　　　a_max = a_max0
　　　Else
　　　　a_min = Application.Max(aa - kizami, a_min0)
　　　　a_max = Application.min(aa + kizami, a_max0)
　　　　kizami = kizami * 0.1
　　　End If
　　　For a = a_min To a_max Step kizami
　　　　b_min = Application.Max(bb - kizami * 10, a)
　　　　b_max = Application.min(bb + kizami * 10, (1 - a) / 3)
　　　　For b = b_min To b_max Step kizami
　　　　　c_min = Application.Max(cc - kizami * 10, b)
　　　　　c_max = Application.min(cc + kizami * 10, (1 - a - b) / 2)
　　　　　For c = c_min To c_max Step kizami
　　　　　　d = 1 - a - b - c
　　　　　　If c <= d And d < 1 Then
　　　　　　　p = (a + 1 / a) * (a + 1 / a) + (b + 1 / b) * (b + 1 / b) + (c + 1 / c) * (c + 1 / c) + (d + 1 / d) * (d + 1 / d)
　　　　　　　If min > p Then
　　　　　　　　min = p
　　　　　　　　aa = a
　　　　　　　　bb = b
　　　　　　　　cc = c
　　　　　　　　Cells(n, 2).Value = min
　　　　　　　　Cells(n, 3).Value = aa
　　　　　　　　Cells(n, 4).Value = bb
　　　　　　　　Cells(n, 5).Value = cc
　　　　　　　　Cells(n, 6).Value = d
　　　　　　　End If
　　　　　　End If
　　　　　Next c
　　　　Next b
　　　Next a
　　Next dankai
End Sub

　同様にマクロm5以降もつくる事が出来る．ただし計算するのに時間がかかるものとなる．

---

NO9「三角定規」9/01 20時11分受信 更新9/4

NO10「中川幸一」9/03: 11時32分受信 更新9/4

「解答」です。