�����P�V�N�P�O���Q�R��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��161�����w�I�ȉ�����m�n�Q
�@�@�@�@�@�@����W���ԁF�X���Q�T���`�P�O���Q�R��
�m�����n
�F����A����̉�����Ԃ͂P�����Ƃ��܂��B�����Ŗ��ł��B
�@�`�a���`�b�̓ӎO�p�`�`�a�b�̓y�n������܂��B���Y����͂`�o�{�a�o�{�b�o�̒������ŏ��ɂȂ�_�o�ɕ߂܂����B
�����܂��Ă���_�o���ǂ����l���Ă��������B�������A���p�ڂa�`�b�͂P�Q�O���ȓ��Ƃ��܂��B
�m�n�X�uKW�v�@�@ 10/16 21��21����M �X�V10/23<br>
���P�@![]() ��
��![]() �̂Ƃ��@
�̂Ƃ��@![]() ��
��![]() �E�E�E�@
�E�E�E�@
�@�����藧��
[�ؖ�]�@���ӂ��Q�悵�ā@![]() ��
��![]() �@
�@
���Ӂ|�E�Ӂ�![]() �|
�|![]()
�@�@�@�@��![]() ��
��![]() ���O
���O
���Q�@�s�����@![]() �{
�{![]() ��
��![]() �@�����藧��
�@�����藧��
[�ؖ�]
�@�����Q��![]()
�@�@�@ ��![]()
�@�E���Q��![]()
�@���@![]() ��
��![]()
���ӂɁ@![]() ��������Ɓ@�����Q���E���Q�@���ؖ������B
��������Ɓ@�����Q���E���Q�@���ؖ������B
�����O�A�����O�̂Ƃ��A�`(�O�C��)�C�a�i���C�O�j�C�b�i�|���C�O�j�Ƃ��C
���`�a�b�̓����܂��͎���̓_�o�i���C���j�ɑ���
 �`�o�{�a�o�{�b�o��
�`�o�{�a�o�{�b�o��
![]() �{
�{![]() �{
�{![]()
�@��![]() �{
�{![]() ��
��![]() �{
�{![]()
���@![]() ��
��![]() �{
�{![]() �@���l�����
�@���l�����
�@�@�@![]() ���|1�{
���|1�{![]() �@�ƂȂ�@
�@�ƂȂ�@![]() �̂Ƃ��ŏ��ɂȂ邱�Ƃ�������
�̂Ƃ��ŏ��ɂȂ邱�Ƃ�������
�����
�`�o�{�a�o�{�b�o�� �ڂa�`�b���P�Q�O���ȓ��ł���@P(�O�C![]() )�@��
)�@��
���`�a�b�̓����܂��͎���̓_�o�ł��邩��C���̓_�ɕ����܂��Ă��邱�ƂɂȂ�B
�m�n�P�O�u�Ӱ��݁v 10/17 19��12����M �X�V10/23<br>
��
�ӎO�p�`ABC������A���߂�_�͕�BC��ɂ���B
AP��ɓ_�������Ƃ��A�Ⴆ�Ώ�ɁA���̓_���o�f�Ƃ���ƁABP',CP'��ɂ��ꂼ��B,C����BP,CP �̒������Ƃ����_��B',C'�Ƃ��A�c��̒�����x �Ƃ���ƁAAP-AP'=y
������A
AP+BP+CP��AP'+BP'+CP'=AP-y+BP+CP+2x �ł�����Ay��2x �ɂȂ��ĂȂ��Ƃ��߂ł��B
�܂�A�������Ƃ��́Ay=2x �̂Ƃ��ŁA�@���̂Ƃ��́ABP=BB' �Ȃ킯������A
���ax �Ɣ��aBB'�Ƃ̉~���ڂ��Ă��邱�ƂɂȂ�B�܂�ABB'��PB'�ƂȂ�܂����A��p�����p�̓ӎO�p�`�͂Ƃ�Ȃ��B
�������ABP��BB'������Ȃ���v����Ζ������B���̂Ƃ��́ABP'��BB'�Ȃ̂ŁA2x=y�����O�p�`�́A��BP'P=60�x�@�ƂȂ�B
���ǁA�_�o�́A��BC�̐���������Ł�BPC=120�x�̓_�B�I
��APB=��APC �����R120�x�ƂȂ�B
������Ƃ����ؖ��ɂȂ��ĂȂ��悤�ł����B
�����ł͊O�S���낤���Ďv���Ă܂������ǂ����ł͂Ȃ��`���ׂ���A��ʓI�ȎO�p�`�ł���APB=��BPC=��CPA=120�x�B�̓_�Ȃ�ł��ˁI�i�V���^�C�i�[�_�j
���H���P�[�u���ȂǍ��Ƃ��厖�ȓ_�ɂȂ��ł��ˁB�i�R�X�g�ʂŁj
�m���P�P�ukasama�v 10/18 19��13����M
�X�V10/23<br>�@
�O�p�`�̒��_��A(xa,ya)�AB(xb,yb)�AC(xc,yc)�A���_P(x,y)���Ƃ���ƁA����AP�ABP�ACP�̘af(x,y)��
�@![]()
�ł��Bf(x,y)�͎O�p�`�̓����ł͘A���Ŕ����\�ŁA
�@![]() �A
�A![]()
�Ȃ̂ŁA�ŏ��l�����݂��܂��B�����āA�ŏ��l��^����̂́A
�@![]() �A
�A![]()
������_�A�܂��͊e���_�ł��B����ƁA
�@![]()
�@![]()
�ł����A
�@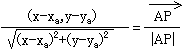 �A
�A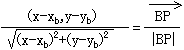 �A
�A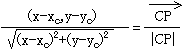
�Ȃ̂ŁA
�@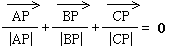
�ƂȂ�܂��B�����͒P�ʃx�N�g���ł����A�a��0�ɂȂ�̂͊e�x�N�g�����Ȃ��p��120߂̏ꍇ�ŁA�e���p��120߂�菬�����ꍇ�A���̂悤�ȓ_�͂�����O�p�`�̓����ɑ��݂��܂��B�@
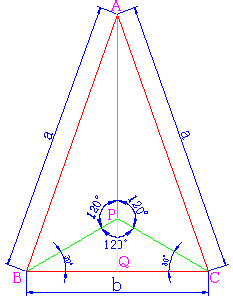
�����ŁA���}�̂悤�ȓӎO�p�`���l���܂��B����ƁAAP+BP+CP�̒������ŏ��ɂȂ�_�͐}�Ɏ������_P�ŁA���̂Ƃ��̍ŏ��l�́A
�@AP+BP+CP=AP+2BP=AQ-PQ+2��(BQ2+PQ2)=��(AB2-BQ2)-PQ+2��(BQ2+PQ2)
�@=��(AB2-BQ2)-BQtan(30�)+2��(BQ2+BQ2tan2(30�))=��3BQ
+ ��(AB2 - BQ2)
�����ŁAAB=a�ABQ=b/2�Atan(30�)=1/��3�Ȃ̂ŁA�ŏ��l�́A
�@��3b/2+��(4a2-b2)/2
�ł��B
�������쐬�A����J�l�ł��B
���̏������܂ő����̂��낤�Ǝv���Ă�����A����10�������Ή߂��A�����ԏH���[�܂蒩���͏����������ł��B����ߕӂ̎R�X�ł͍g�t���n�܂낤�Ƃ��Ă��܂��B
���āA������ʔ������ł��ˁB
�ȑO�A�ǂ����̋��{�ԑg�̂悤��(�Ƃ͂�����ƌ�����ł���)�o���G�e�B�ԑg�ŁA���w�҂̏H�R�m���Ə��D�̋e��悳����Ǝ����悤�Ȗ��̓����������o������������Ă܂����B�����ȓ̔��R���S�{�̖_�łȂ��Ƃ߁A�̊ԂɃV���{���t�𗬂����ނƁA�V���{���̖����_�Ɩ_�����ԍŒZ�o�H��ɒ�����悤�ł��B�V���{�����͂ł��邾���������Ȃ낤���鐫�������邻���ŁA����𗘗p���Ă���̂��Ƃ������Ă܂����B
�����̗���F�R�����g���@�����ł��B�e���r�Ŏ����ςĂ��܂����B���R�̒��ɓ������B����Ă����P�ł��B
![]()
