�����P�X�N�R���P�W��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��1�W�V�����w�I�ȉ������
�@�@�@�@�@�@����W���ԁF�Q���Q�T���`�R���P�W��
�m���������ԁn
�F����̓E�H�[�L���O�����܂��B�W�����̋������A�ŏ��̒n�_�Ŏ����U�����A
�Ō�̓����n�_�ł͎����S�����ɂȂ�A�r���̎����́A������������1������
�\�����悤�ɃE�H�[�L���O����Ƃ��A���������Ԃ����߂Ă��������B
���R�����g�F���̃E�H�[�L���O�͂܂����������Ă��������B��߂�͍l���Ă��܂���B��
�@�i25���ߌ�5���lj��j
�m�n�P�uuchinyan�v02/25 13��29����M �X�V3/18
��P�W�V�w�I�ȉ�����
�m���������ԁn
�o���n�_�����_ O �Ƃ��C�����n�_�� x ���̐��̕����ɂȂ�悤�ɍ��W�����܂��B
�����āC�o�����Ă��� t ���Ԍ�̈ʒu�� x(t) �Ƃ��܂��B
�����ł�����ƋC�ɂȂ�̂ł����C�ʏ�̃E�H�[�L���O�͌�߂�Ƃ��͂��Ȃ��̂ł������肵�܂��B
���ہC��߂�������ƁC���܂ł����Ă������n�_�ɒ����Ȃ����Ƃ��\�ŁC���ɂȂ�܂��� (^^;
���̉���̉��ł́Ct ���Ԍ�̈ʒu x(t) �������������ɂȂ�܂��B
�����ŁCt ���Ԍ�̎��� v(t) �́C
v(t) = a * x(t) + b
�܂��C�o�����_�̏�������
t = 0 �� x(0) = 0, v(0) = 6 �Ȃ̂�
b = 6
���ɁCT ���Ԍ�ɓ����n�_�ɒ������Ƃ���ƁC
t = T �� x(T) = 8, v(T) = 4 �Ȃ̂�
8a + b = 4
���ꂩ��Ca = - 1/4�Cb = 6 �Ȃ̂ŁC
v(t) = - 1/4 * x(t) + 6
�����͈ʒu�̎��Ԕ����Ȃ̂�
dx/dt = v(t) = - 1/4 * x + 6
1/(- 1/4 * x + 6) * dx/dt = 1
���ӂ� t �� 0 �` T �͈̔͂Őϕ�����
��[0,T]{1/(- 1/4 * x + 6)} * dx/dt
* dt = ��[0,T]{1}dt
T = ��[0,8]{1/(- 1/4 * x + 6)}dx
= [- 4 * log(- 1/4 * x + 6)][0,8]
= {- 4 * log(- 1/4 * 8 + 6)} - {- 4 * log(- 1/4 * 0 + 6)}
= - 4 * log(4) + 4 * log(6)
= 4 * log(3/2)
= 1.62186�c
�` 1.622 ����
�܂�C���������Ԃ́C�ق� 1.622 ���� = 1 ���� 37 �� 19 �b �` 1 ���� 37 �� �ɂȂ�܂��B
(���z)
��L�̉���
�@�����ł�����ƋC�ɂȂ�̂ł����C�ʏ�̃E�H�[�L���O�͌�߂�Ƃ��͂��Ȃ��̂ł������肵�܂��B
������������ƈ���������̂ł����C���ɂ��������悤�ɁC������߂�������ƂȂ�ƁC
���������Ԃ�������C�Ƃ������Ƃ��\�Ȃ̂ŁC�l�����܂���ł����B
����ł悩�����̂ł���ˁD�D�D�H (^^;
��������ł����̂Ȃ�C�����������̎育��ȕ��K���Ǝv���܂��B
�Ȃ��C��G�c�ɁC6km/h �� 4km/h �̕��� 5km/h �� 8km ���s�����Ƃ���ƁC8/5 = 1.6 ���ԂŁC
����ł��قڈ�v���܂��ˁB
�m�n�Q�ukashiwagi�02/26 12��46����M �X�V3/18
���R�����g�F�����b�ɂȂ�܂��B����̖��͑�D���Ȕ����������̖��ŁA���� �ǂ݂Ȃ���A�����^�ɂ���Ή�����ȂƁA��@��������ŎQ��܂����B
�@���Ɋy���݂Ȃ�������܂������A8������1����40�����X�Ƃ͑����ł��ˁB
187����
�@���A���x��V�A������X�A���Ԃ�T�Ƃ���ƁA��ӂ��
�@�@�@�@V�@���@��X/��T�@���@AX+B�@�E�E�E�E�E�E�@�����藧�B
���A�����ƏI�����e�X6�q/H�A4�q/H�x�擪�̐���4�ł��邩��
�@�@�@�@�@B�@=�@6�@�@�@8A�@+�@6�@���@4�@���������AA�@���@-1/4�@�ƂȂ�B
�����AV�@���@�i-1/4�jX�@+�@6�@�E�E�E�E�E�A�ƂȂ�B
�@�ƇA���@��X/��T�@���@�i-1/4�jX�@+�@6�@
�����A�@��X/�i-1/4�jX�@+�@6�@���@��T�@�E�E�E�E�E�B�@����������B
�����āA���ӂ��e�XX��T�Őϕ�����ƁA
T�@���@![]() �@���@4log�i3/2�j�@���@�P�D�U�Q���ԁ@
�@���@4log�i3/2�j�@���@�P�D�U�Q���ԁ@
�@�@�@�@
�@�����A��1���ԂR�V�������������ƂɂȂ�B
�m�n�R�u�V�o�l�����v02/26 16��51����M �X�V3/18
���R�����g�F��P�W�U��̉W�̃A�b�v�y�����q�������Ă��������܂����B
�F����̉̃G���K���g���Ɉ��R�I�I
�u�������ԁv�̖����y�����l�������Ē����܂����B���̊p�x�Ŗ��쐬�\�ȏ��ɍĂш��R�I�I
��P�W�V��̉���������Ē����܂��B�敪���ϖ@�������������p���܂����B�s�\���ȂƂ��낪��������܂����A
�܂��͂����肵�܂��B
�@
�u�V�o�l�����v02/27 13��07����M �X�V3/18
�����������H�@�����Ǝ��ԂƑ����̊W�Ȃ̂�����c�c
����Ⴛ�����I���w���Ėʔ������s�v�c�c�c
�@
�m�n�S�u���[��v02/26 17��32����M �X�V3/18
���R�����g�G�����������A�v���Ԃ�ɉ����܂����O�O�G��
������������x�C���Ԃ�t�Ƃ����ƁC��ӂ��C
![]()
�Ƃ�����
�����ŁC���E�����F![]() �C
�C![]() �@�������āC
�@�������āC
![]() �C
�C![]()
�]���āC
![]()
�ϐ������@�ɂ��ϕ�����ƁC

![]() �@�i�������Ac�͐ϕ��萔�j
�@�i�������Ac�͐ϕ��萔�j
���������F![]() ���C
���C![]()
�]���āC

x = 8�������āC���߂�t�́C
![]()
���Ȃ݂ɁCx < 24�Ƃ���x�ɂ��ĉ����ƁC
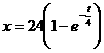
�ƂȂ�C���̕���������24 km�n�_�ɂ͉i�v�ɂ��ǂ蒅���Ȃ����ƂɂȂ�܂��ˁB
�m�n�T�uToru�v 03/01 11��41����M �X�V3/18
��P�W�V��𑗂�܂��B�����������Ȃ�Ăق�ƂɂЂ����Ԃ�Ƃ��������ł����B
���Z�ł͂ǂ̒��x�K����ł��������H�@�@
�����̗���R�����g�F���݂̊w�K�w���ł́u���w�V�v�Ŕ����������𗚏C���܂��B��
����������t�̊��Ƃ��ā@x(t) �@�Ƃ�
�������dx/dt =ax+b �Ƃ����
x=0�@�̎��@dx/dt =6
x=8�@�̎��@dx/dt=4
����b=6 , 4=8a+b �Ł@a=-1/4 , b=6
d(x-24)/dt=-1/4 (x-24) �ƕό`����
x-24=C e^(-t /4 ) t=0, x=0 �Ƃ���C=-24���
x=24(1- e^(-t /4 ))�@x=8�Ƃ����e^(-t
/4) =2/3 ���t=4(log3-log2)�@�i���ԁj
4(log3-log2)=1.62186043--���P���ԂR�V���P�W�b6975-- �ƂȂ�܂����B���ώ���
�Tkm��1.6 ���Ԃł����炾����������Ȃ��̂ł悳�����ȋC�����܂��B
�m�n�U�u�O�p��K�v 03/04 19��44����M �X�V3/18
���R�����g�F������͔q�����Ă���̂ł����C���������C�G���ɖZ�E����Ă��ĉ�����Ă���]�T���Ȃ�������ŁC����v���Ă���܂����B
����̖��ł����C����������̃z�[���O���E���h�ŁC����͐���˂Ǝv���܂����B��

�m�n�V�u�ukasama�v�v 03/08 20��39����M �X�V3/18
�w�r���̎����́A������������1�����x�Ȃ̂ŁA����v�A����x�Ƃ���ƁA
�@v=6+(4-6)x/8=6-x/4�ł��B
����x�͎���t�̊��ƍl�����A���̔��W��������������Av=dx/dt�ł��B����ƁA���
�@dx/dt=6-x/4�ƂȂ�܂��B
���̔����������������ƁA-4log(24-x)=t+C(�萔)
�ƂȂ�܂��B��������t=0�̂Ƃ�x=0�����Ă͂߂�ƁAC=-4log(24)�ł�����A
�@t=4log{24/(24-x)}�ł��B
�����x=8��������ƁAt=4log(3/2)�ł�����A���������Ԃ́A
�@4log(3/2)=1.62186����ł��B
![]()
