平成19年11月4日
 [流れ星]
[流れ星]
第198回数学的な応募問題解答
<解答募集期間:10月14日~11月4日
[フーリエ級数(2)]
皆さん、ゼーター関数をご存知ですか。前回の問題はフーリエ級数とζ(2)の関係でしたが、今回も同じです。ζ(2)に求め方の別解とζ(4)にチャレンジください。

NO1「kashiwagi」10/15 08時08分受信 更新11/4
<コメント:期待していたフーリエ級数(2)がでていたので早速トライ致しました。
しかし、何回解いてもフーリエ級数は楽しいですね。学生時代の興味が体の内奥に残って
いる感じです。少々簡略説明ですが。>
198回問題
問1.及び問2.
式②を-π~πまで積分する。

計算すると、![]() となり、
となり、![]() である。
である。
式②をXで微分すると、 ![]()
この式は前回の式①と同じであるから 類推して![]() となる。因って、
となる。因って、
![]() となる。これより
となる。これより![]() となる。
となる。
問3.上記より、
![]() であるから、Xにπを代入し、
であるから、Xにπを代入し、
![]() を得る。因って
を得る。因って![]()
問4.式②を平方し、三角関数の直交性(2)や(3)を使い両辺を積分すると、
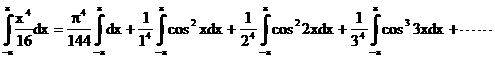
![]() であるから、
であるから、
![]() が求めるものである。
が求めるものである。
NO2「uchinyan」10/15 12時52分受信 更新11/4
<コメント:計算が面倒そうなので確かめてはいませんが,原理的には,
同様の計算を繰り返せば,ζ(2n) の値を順次求められそうです。
一方,ζ(2n-1) は,ナイーブにはうまくいきそうになさそうですね。>
第198回数学的な応募問題
[フーリエ級数(2)]
今回の問題は前回の延長のような感じもあり,前回証明した三角関数の直交性は仮定します。
特に,次を使用します。
m, n を m, n >= 0 なる整数とします。
∫[-π~π] cos(mx)cos(nx)
dx
= 0 m not= n の場合
= π m = n not= 0 の場合
= 2π m = n = 0 の場合
また,前回と同様に,
(A) この無限和内の順序交換は可能
(B) この無限和と積分の順序交換は可能
も仮定し,今回は特に断らずに使用します。
問題1:& 問題2:
x^2/4 = a(0)/2 + Σ[m=1,∞] a(m) * cos(mx)
等式の両辺の x を -π~π で積分すると,
∫[-π~π] {x^2/4} dx = ∫[-π~π] {a(0)/2 + Σ[m=1,∞] a(m) * cos(mx)} dx
右辺 = ∫[-π~π] {a(0)/2 + Σ[m=1,∞]
a(m) * cos(mx)} dx
= a(0)/2 * ∫[-π~π] {1} dx +
Σ[m=1,∞] a(m) * ∫[-π~π] {cos(mx)} dx
= a(0)/2 * 2π
左辺 = ∫[-π~π] {x^2/4} dx
= 2 * ∫[0 ~π] {x^2/4} dx
= 2 * [x^3/12][0 ~π]
= 2 * π^3/12
そこで,
a(0)/2 = π^2/12
さらに,等式の両辺に cos(nx),n = 1, 2, 3, ...,を掛けて,x を -π~π で積分すると,
∫[-π~π] {x^2/4 * cos(nx)} dx = ∫[-π~π] {a(0)/2 + Σ[m=1,∞] a(m) * cos(mx)} * cos(nx)
dx
右辺 = ∫[-π~π] {a(0)/2 + Σ[m=1,∞]
a(m) * cos(mx)} * cos(nx) dx
= a(0)/2 * ∫[-π~π] cos(nx) dx + Σ[m=1,∞] a(m) * ∫[-π~π] cos(mx)cos(nx) dx
= a(n) * π
左辺 = ∫[-π~π] {x^2/4 * cos(nx)} dx
= ∫[0 ~π] {x^2/2 * cos(nx)} dx
= [x^2/2 * sin(nx)/n][0 ~π] -
∫[0 ~π] {x * sin(nx)/n} dx
= - [1/n * x * (- cos(nx)/n)][0
~π] - 1/n * ∫[0 ~π] {cos(nx)/n} dx
= π * (-1)^n/n^2 - 1/n * [1/n * sin(nx)/n][0 ~π]
= π * (-1)^n/n^2
そこで,
a(n) = (-1)^n/n^2, n = 1, 2, 3, ...
特に,
a(1) = - 1, a(2) = 1/4
問題3:
問題1:& 問題2:より,
x^2/4 = π^2/12 + Σ[m=1,∞] (-1)^m/m^2 * cos(mx)
と書けます。そこで,x = π とおくと,
π^2/4 = π^2/12 + Σ[m=1,∞] (-1)^m/m^2 * cos(mπ)
π^2/4 - π^2/12 = Σ[m=1,∞] (-1)^m/m^2 * (-1)^m
Σ[m=1,∞] 1/m^2 = π^2/4 - π^2/12 = π^2 * 2/12 = π^2/6
Σ[n=1,∞] 1/n^2 = π^2/6
になります。
問題4:
x^2/4 = π^2/12 + Σ[m=1,∞] (-1)^m/m^2 * cos(mx)
において,両辺を二乗して,x を -π~π で積分すると,
(x^2/4)^2 = (π^2/12 + Σ[m=1,∞] (-1)^m/m^2 * cos(mx))^2
x^4/16
= π^4/144 + 2 * π^2/12 * Σ[m=1,∞] (-1)^m/m^2 * cos(mx)
+ (Σ[m=1,∞] (-1)^m/m^2 * cos(mx))^2
x^4/16
= π^4/144 + 2 * π^2/12 * Σ[m=1,∞] (-1)^m/m^2 * cos(mx)
+ Σ[m=1,∞ & n=1,∞] {(-1)^m/m^2
* (-1)^n/n^2 * cos(mx) * cos(nx)}
∫[-π~π] {x^4/16} dx
= ∫[-π~π] {π^4/144} dx
+ ∫[-π~π] {2 * π^2/12 *
Σ[m=1,∞] (-1)^m/m^2 * cos(mx)}
dx
+ ∫[-π~π] {Σ[m=1,∞ & n=1,∞] {(-1)^m/m^2 * (-1)^n/n^2 * cos(mx) * cos(nx)}
dx
右辺
= ∫[-π~π] {π^4/144} dx
+ ∫[-π~π] {2 * π^2/12 * Σ[m=1,∞] (-1)^m/m^2 * cos(mx)} dx
+ ∫[-π~π] {Σ[m=1,∞ & n=1,∞]
{(-1)^m/m^2 * (-1)^n/n^2 * cos(mx)
* cos(nx)} dx
= π^5/72
+ 2 * π^2/12 * Σ[m=1,∞] (-1)^m/m^2 * ∫[-π~π] {cos(mx)} dx
+ Σ[m=1,∞ & n=1,∞] {(-1)^m/m^2 * (-1)^n/n^2 * ∫[-π~π] cos(mx)cos(nx) dx}
= π^5/72
+ 0
+ Σ[n=1,∞] {(-1)^n/n^2 * (-1)^n/n^2 * π}
= π^5/72
+ π * Σ[n=1,∞] 1/n^4
左辺 = ∫[-π~π] {x^4/16} dx
= ∫[0 ~π] {x^4/8} dx
= [x^5/40][0 ~π]
= π^5/40
そこで,
π^5/40 = π^5/72 + π * Σ[n=1,∞] 1/n^4
Σ[n=1,∞] 1/n^4 = π^4/40 - π^4/72 = π^4 * (9 - 5)/360 = π^4 * 4/360
Σ[n=1,∞] 1/n^4 = π^4/90
になります。
(考察)
同様の計算を,例えば x^3/6 に行って,ζ(2) =
π^2/6,ζ(4) = π^4/90 を使うと,
ζ(6) = π^6/945 が求まります。
それ以上は大変そうなので計算していませんが,適当な関数を使って,順次,ζ(2n) を求めていけそうです。
一方,ζ(2n-1) は,ちょっと考えた感じでは,うまく行きそうにはなさそうですね。
(感想)
前回と同様に,ζ関数の値が簡単に求まってしまうのには驚きです。
いずれにせよ,フーリエ級数を使っていろいろな級数の和が求まりそうなのは,
興味深いことだと思いました。
NO3「新俳人澄朝」10/16 18時03分受信 更新11/4

NO4「bear56」 10/16 19時56分受信
更新11/4

NO5「Toru」 10/22 14時11分受信 更新11/4
<コメント:細かいところは目をつぶって、結果のきれいなところを楽しむことにします。
また時間がとれたら、解析概論を読みなおしてみます。 >
問題1、2
?の両辺を-π~πまで積分すると
左辺:・(x^2/ 4)dx=[x^3/12]=π^3
/6
右辺は初項以外は0になって
右辺:・(a0 /2) dx=a0π よりa0 /2=π^2 /12
cos nx (n=1,2,----)をかけて同様に積分すると
左辺:・(x^2 cos nx /4)dx=[x^2 sin nx /4n] -・( x sin nx /2n)dx
=[x cos nx /2n^2]+・cos nx /2n^2 dx=(-1)^2 π/n^2+[sin nx /2n^3]
=(-1)^n π/n^2
右辺はa nの項以外は0になって
右辺:・a n(cos nx)^2dx =πan
これからan=(-1)^n/ n^2 (a1=-1,a2=1/4)
問題3 f(x)=x^2/4 (-π≦x≦π)を周期2πの周期関数として拡張すると、これはX=π
で連続であるから、
?でx=πとすると
π^2/4=π^2/12 + Σ(-1)^n cos nπ/n^2=π^2/12 + Σ(1/n^2)
よりΣ(1/n^2)=π^2/4-π^2/12 =π^2 / 6
問題4
・(x^4/16)dx=[x^5/80]=π^5/ 40
右辺を2乗して展開し項別積分できるとすれば、各項の2乗以外のものはすべて0にな
り
・(a0 /2)^2 dx=a0^2 π/2=π^5
/72
・(an cos nx)^2dx
=πan^2=π/ n^4 これらから
π^5/ 40=π^5 /72+Σ(π/n^4)
よってΣ(1/n^4)=π^4/40 - π^4
/72=π^4 /90
NO6「ぐーてん」10/23 16時07分受信 更新11/4
<コメント:今回もフーリエ級数の基礎的なところが勉強できてためになりました。
実はフーリエ変換の方は仕事で多用しています。
どんな時に使うかというと、私の仕事は研究ですので、実験をやって自動測定して得られた時系列データ(温度、重量、動力などさまざま。。)から細かい変動を取り除いて、データを平滑化するために用います。実験で得たデータをフーリエ変換してパワースペクトルを求め、そのうち除去したい周波数成分を0に書き換え、さらに逆変換をすると元のデータが平滑化されたものが得られます。
昔は、プログラムを書いて計算させたり、専用の解析ソフトが必要でしたが、今はエクセルだけで簡単にできてしまいます。便利な世の中になりました。>
<水の流れ:応募されたこのときの解答は、一部修正がありましたから、その後の解答を下に掲載しました。>
「ぐーてん」10/29 11時27分受信 更新11/4
問題1
②式の両辺を![]() から
から![]() まで積分すると,
まで積分すると,
![]() .
.
右辺の余弦の項は積分すると全て0なので定数項だけのこり,![]() .よって,
.よって,![]() .
.
②式の両辺に![]() ,
,![]() をかけてそれぞれ
をかけてそれぞれ![]() から
から![]() まで積分すると,
まで積分すると,
![]() ,
,
![]() .
.
右辺は2乗の項だけがのこり,![]() ,
,![]() .よって,
.よって,![]() ,
,![]() .
.
問題2
②式の両辺に![]() をかけて
をかけて![]() から
から![]() まで積分すると,
まで積分すると,
![]() .
.
同様に右辺は2乗の項だけのこり,![]() .よって,
.よって,![]() .
.
問題3
②式を書き直すと,![]() .
.
![]() を代入して,
を代入して,![]() .よって,
.よって,![]() .
.
問題4
②式より,![]() .
.
両辺を2乗して![]() から
から![]() まで積分すると,
まで積分すると,
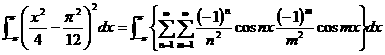
右辺の![]() の項は消えて2乗の項だけのこり,
の項は消えて2乗の項だけのこり,![]() .よって,
.よって,![]() .
.
NO7「kasama」 11/01 23時04分受信
更新11/4
|
問題1 順次フーリエ係数を求めると、次のようになります。 |
|
|
|
|
|
|
|
問題2 前問より、(-1)n/n2と推測できます。実際にやってみると、次のようになります。 |
|
問題3 ②式に上で求めた係数を適用すると、 |
|
問題4 題意により②式を2乗すると、 |
![]()
