�����Q�O�N�V���P�R��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��Q�O�X�����w�I�ȉ�����
�@�@�@�@�@�@����W���ԁF�U���P�T���`�V���P�R��
�m�ݏ�a�̋Ɍ��n
�F����A�ߋ��̑�w�����������Ă�����A���̂悤�Ȗ�肪�łĂ��܂����B

NO1�uuchinyan�v 6/15 12��12����M
�uuchinyan�v 6/15 18��15����M
�X�V7/13
��Q�O�X�w�I�ȉ�����
�m�ݏ�a�̋Ɍ��n
a(n) = (1 + 2^2 + 3^3 + ... + n^n)/(n + 1)^n
(1)
a(1) = 1/(1 + 1)^1 = 1/2^1 = 1/2 = 0.5
a(2) = (1 + 2^2)/(2 + 1)^2 = (1 + 4)/3^2 = 5/9 =
0.5555...
a(3) = (1 + 2^2 + 3^3)/(3 + 1)^3 = (1 + 4 + 27)/4^3
= 32/64 = 1/2 = 0.5
a(4) = (1 + 2^2 + 3^3 + 4^4)/(4 + 1)^4 = (1 + 4 +
27 + 256)/5^4 = 288/625 = 0.4608
a(5) = (1 + 2^2 + 3^3 + 4^4 + 5^5)/(5 + 1)^5 = (1 +
4 + 27 + 256 + 3125)/6^5 = 3413/7776 = 0.4389...
(2)
n >= 6 �̐����ɑ��āC
1 - a(n)
= 1 - (1 + 2^2 + 3^3 + ... + n^n)/(n + 1)^n
= {(n + 1)^n - (1 + 2^2 + 3^3 + ... + n^n)}/(n +
1)^n
= {n^n + nC1 * n^(n-1) + nC2 * n^(n-2) + ... +
nC(n-2) * n^2 + nC(n-1) * n + 1) - (1 + 2^2 + 3^3 + ... + n^n)}/(n + 1)^n
= {(nC1 * n^(n-1) - (n-1)^(n-1)) + (nC2 * n^(n-2) -
(n-2)^(n-2)) + ... + (nC(n-3) * n^3 - 3^3) + (nC(n-2) * n^2 - 2^2) + nC(n-1) *
n}/(n + 1)^n
= {��[k=1,n-2]{nCk * n^(n-k) - (n-k)^(n-k)} + nC(n-1) * n}/(n + 1)^n
�����ŁCn > k >= 1 �̐����̂Ƃ��C���炩�ɁC
n > n-k > 0, nCk > 1
nCk * n^(n-k) > n^(n-k) > (n-k)^(n-k)
nCk * n^(n-k) - (n-k)^(n-k) > 0
nC(n-1) * n > 0
�Ȃ̂ŁCn >= 6 �̐�����
1 - a(n) > 0
a(n) < 1
�ɂȂ�܂��B�܂��C(1)���Cn = 1, 2, 3, 4, 5 �ɑ��Ă� a(n) < 1 �ł��B
���ǁC���ׂĂ̎��R�� n �ɑ���
a(n) < 1
�������܂��B
(3)
a(n+1)
= (1 + 2^2 + 3^3 + ... + n^n + (n + 1)^(n + 1))/(n
+ 2)^(n + 1)
= (1 + 2^2 + 3^3 + ... + n^n + (n + 1)^(n + 1))/(n
+ 1)^n * (n + 1)^n/(n + 2)^(n + 1)
= {(1 + 2^2 + 3^3 + ... + n^n)/(n + 1)^n + (n +
1)^(n + 1)/(n + 1)^n} * (n + 1)^n/(n + 2)^(n + 1)
= {a(n) + (n + 1)} * (n + 1)^n/(n + 2)^(n + 1)
= a(n) * (n + 1)^n/(n + 2)^(n + 1) + (n + 1)^(n +
1)/(n + 2)^(n + 1)
(4)
���炩�ɁC0 < a(n) �Ȃ̂ŁC0 < a(n) < 1 ���
0 <= lim[n->��]{a(n)} <= 1
�ŁClim[n->��]{a(n)} �͗L�E�ł��B
(3)���C
a(n+1) = a(n) * (n + 1)^n/(n + 2)^(n + 1) + (n +
1)^(n + 1)/(n + 2)^(n + 1)
lim[n->��]{a(n+1)} = lim[n->��]{a(n) * (n + 1)^n/(n
+ 2)^(n + 1) + (n + 1)^(n + 1)/(n + 2)^(n + 1)}
= lim[n->��]{a(n)} * lim[n->��]{(n + 1)^n/(n + 2)^(n
+ 1)} + lim[n->��]{(n + 1)^(n + 1)/(n + 2)^(n + 1)}
�����ŁC
(n + 1)^n/(n + 2)^(n + 1)
= (n + 1)^n/((n + 1) + 1)^(n + 1)
= (n + 1)^n/{(n + 1)^(n + 1) * (1 + 1/(n + 1))^(n +
1)}
= 1/(n + 1) * 1/(1 + 1/(n + 1))^(n + 1)
lim[n->��]{(n + 1)^n/(n + 2)^(n + 1)}
= lim[n->��]{1/(n + 1) * 1/(1 + 1/(n + 1))^(n + 1)}
= lim[n->��]{1/(n + 1)} * lim[n->��][1/(1 + 1/(n +
1))^(n + 1)}
lim[n->��](1 + 1/(n + 1))^(n + 1) = lim[n+1 -> ��]{(1
+ 1/(n + 1))^(n + 1)} = e (���R�ΐ��̒�)�Ȃ̂ŁC
lim[n->��]{(n + 1)^n/(n + 2)^(n + 1)}
= 0 * 1/e
= 0
�܂��C
(n + 1)^(n + 1)/(n + 2)^(n + 1)
= (n + 1)^(n + 1)/((n + 1) + 1)^(n + 1)
= 1/(1 + 1/(n + 1))^(n + 1)
lim[n->��]{(n + 1)^(n + 1)/(n + 2)^(n + 1)}
= lim[n->��]{1/(1 + 1/(n + 1))^(n + 1)}
= 1/e
��������̂ŁC0 <= lim[n->��]{a(n)} <= 1 �ɂ����ӂ��āC
lim[n->��]{a(n+1)} = lim[n->��]{a(n)} * 0 + 1/e = 0
+ 1/e = 1/e
�܂�C
lim[n->��]{a(n)} = 1/e
�ɂȂ�܂��B
(���z)
���ƂȂ�����ł����̂��ȁC�Ƃ�������������̂ł����C���ʂ͈ꉞ���ꂢ�Ȃ̂ŁB
�������C�����ł� 1/e �������Ƃ́D�D�D
NO2�uUnderbird�v 6/19 09��03����M
�X�V7/13
��Q�O�X��@�u�ݏ�a�̋Ɍ��v�@�@Underbird���
![]() �@�Ƃ���Ƃ��A
�@�Ƃ���Ƃ��A
�i�P�j![]() �̒l�����߂�B
�̒l�����߂�B
![]() �@�C�@
�@�C�@![]() �@�C�@
�@�C�@![]() �@�C�@
�@�C�@![]() �C
�C
![]()
�i�Q�j�s���� ![]() ���ؖ�����B
���ؖ�����B
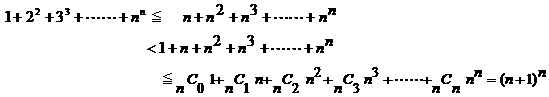
�@ ����āA![]() �@�@���Ȃ킿�A
�@�@���Ȃ킿�A![]() �����藧�B
�����藧�B
�i�R�j![]() ��
��![]() ��
��![]() �p���ĕ\���B
�p���ĕ\���B
�@�@![]()
�@�@�@�����ŁA![]() ���
���![]() ������
������
�@�@![]()
�i�S�j![]() �����߂�B�@
�����߂�B�@
���炩��![]() �Ɓi�Q�j�̌��ʂƂ��킹�āA
�Ɓi�Q�j�̌��ʂƂ��킹�āA![]() �ł��邱�Ƃ���A�i�R�j���
�ł��邱�Ƃ���A�i�R�j���
![]() �@�����藧���A���[�̍��̋Ɍ��l�����ꂼ��v�Z�����
�@�����藧���A���[�̍��̋Ɍ��l�����ꂼ��v�Z�����
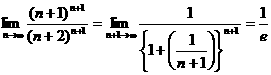
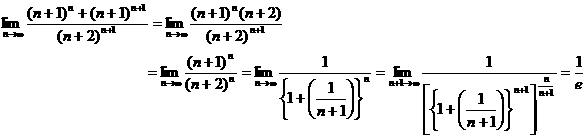 �@�@�@����āA�͂��݂����̌������@
�@�@�@����āA�͂��݂����̌������@![]() �@�@
�@�@
�@
NO3�ukashiwagi�v 6/23 18��00����M
�X�V7/13
209���
�i1�j��ӂ��
![]() �ł��邩�炎��1�E�E�E�E�E�A5��������
�ł��邩�炎��1�E�E�E�E�E�A5��������
![]() �@
�@![]() �@
�@![]() �@
�@![]() �@
�@![]() �@�ƂȂ�B
�@�ƂȂ�B
�i2�jn��1�̎��i1�j���![]() ����������B
����������B
�@�@�������̎����藧�Ƃ���ƁA![]() �@�E�E�E�E�E�@
�@�E�E�E�E�E�@
�Ƃ���ŁA�@���![]() �@�����藧�B���ӂ�
�@�����藧�B���ӂ�![]() ���������
���������![]()
�����āA���ӂ�![]() �Ŋ���ƁA
�Ŋ���ƁA
![]() �@�E�E�E�E�A�@����������B
�@�E�E�E�E�A�@����������B
�����āA�A�[�@�ŏؖ����ꂽ�B
�i3�j�@�ƇA�̊W����@![]() �@�E�E�E�E�E�B�@�ƂȂ�B
�@�E�E�E�E�E�B�@�ƂȂ�B
�i4�j�B���![]() �̋Ɍ����Ƃ�ƁA
�̋Ɍ����Ƃ�ƁA
![]()
������![]() �@�ł��邩��A�㎮��ό`���v�Z����ƁA
�@�ł��邩��A�㎮��ό`���v�Z����ƁA![]() �Ɏ�������B
�Ɏ�������B
�����A![]() �@�ł���B
�@�ł���B
NO4�u�O�p��K�v 6/29 23��52����M �X�V7/13
[���209] �� <�O�p��K>
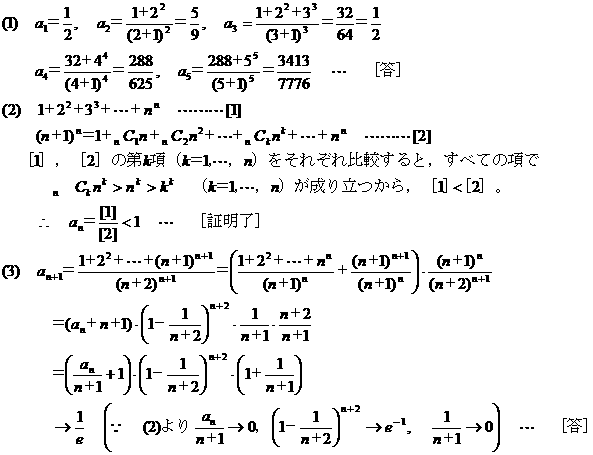
NO5�ukasama�v 7/12 16��37����M �X�V7/13
|
(1)�����v�Z����ƁA |
|
�@a1=1/2,a2=5/9,a3=1/2,a4=288/625,a5=3413/7776 |
|
�ƂȂ�܂��B |
|
(2)an�̕����藝�𗘗p���ĕό`����ƁA |
|
�@(1+n)n=nCn1nn0+nC11n-1n1+nC21n-2n2+�c+nCn1n-nnn��n0+n1+n2+�c+nn>11+22+�c+nn |
|
�ƂȂ�܂�����A |
|
�@an=(11+22+�c+nn)/(n+1)n<1 |
|
�ł��B |
|
(3)an+1��ό`���Ă��ƁA |
|
�@an+1=(11+22+�cnn+(n+1)n+1)/(n+2)n+1={(n+1)nan+(n+1)n+1}/(n+2)n+1=(n+1)n(an+n+1)/(n+2)n+1 |
|
�ƂȂ�܂��B |
|
(4)(3)���A |
|
�@an=nn-1(an-1+n)/(n+1)n |
|
�ł����A0<an-1<1�Ȃ̂ŁA |
|
�@nn-1(0+n)/(n+1)n<an<nn-1(1+n)/(n+1)n��1/(1+1/n)n<an<1/(1+1/n)n�(1+1/n) |
|
�ƂȂ�An�����̂Ƃ����ӂ�1/e�ɂȂ�̂ŁA |
|
�@liman=1/e |
|
�ł��B |
![]()
