�����Q�P�N�S���P�Q��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��Q�Q�Q�����w�I�ȉ������
�@�@�@�@�@�@����W���ԁF�R���Q�Q���`�S���P�Q��
�m�������̗]��n
����A�u��w�ւ̐��w�v�i2009�N3�����j��ǂ�ł��āA���̂悤�Ȗ����l���܂����B
���P�F3������(��)�����R�|�R���Q�|�U���{�T�ɂ��āA
�i�P�j��(��)�����f(��)�Ŋ������]������߂�B
�i�Q�j��(��)�ɂ͋ɒl���Ƃ�_��2���邪�A����2�_��ʂ钼���̕����������߂�B
���Q�F��(��)���|���S�{�S���R�{�U���Q�|�S���ɂ���
�i�P�j��(��)�����f(��)�Ŋ������]������߂�B
�i�Q�j��(��)�ɂ͋ɒl���Ƃ�_���R���邪�A���̂R�_��ʂ�������̕����������߂�B
���R�@��̖��P�Ɩ��Q�ɂ����āA�i�P�j�Ɓi�Q�j�̓����������ł��闝�R���l�@����B
NO1�uuchinyan�v 3/22 14��30����M
�X�V4/12
��Q�Q�Q�w�I�ȉ�����
�m�������̗]��n
�����Ȃ���R�F����ł��ł��܂����C���Ԃɂ���Ă݂܂��B
���P�F
f(x) = x^3 - 3x^2 - 6x + 5
(1)
f'(x) = 3x^2 - 6x - 6
f(x) = (x/3 - 1/3)(3x^2 - 6x - 6) + (- 6x + 3)
�Ȃ̂ŁC�]��� - 6x + 3 �ł��B
(2)
f'(x) = 3x^2 - 6x - 6 = 3(x^2 - 2x - 2) = 3(x - (1 - sqrt(3)))(x - (1 +
sqrt(3)))
�Ȃ̂ŁC
x < 1 - sqrt(3) �ŁCf'(x) > 0�Cf(x) �͒P������
x = 1 - sqrt(3) �ŁCf'(x) = 0�Cf(x)
�͋ɑ�l - 3 + 6 * sqrt(3)
1 - sqrt(3) < x < 1 + sqrt(3) �ŁCf'(x) < 0�Cf(x) �͒P������
x = 1 + sqrt(3) �ŁCf'(x) = 0�Cf(x)
�͋ɏ��l - 3 - 6 * sqrt(3)
1 + sqrt(3) < x �ŁCf'(x) > 0�Cf(x) �͒P������
�Ȃ̂ŁCy = f(x) �́C
(1 - sqrt(3), - 3 + 6 * sqrt(3)), (1 + sqrt(3), - 3 - 6 * sqrt(3))
�ŋɒl���Ƃ�܂��B�����ŁC���̂Q�_��ʂ钼���́C
y - (- 3 + 6 * sqrt(3))
�@= {(- 3 - 6 * sqrt(3)) - (- 3 + 6 * sqrt(3))}/{(1 +
sqrt(3)) - (1 - sqrt(3))} * (x - (1 - sqrt(3)))
y = (- 12 * sqrt(3))/(2 * sqrt(3)) * (x - (1 - sqrt(3))) + (- 3 + 6 * sqrt(3))
y = (- 6) * (x - (1 - sqrt(3))) + (- 3 + 6 * sqrt(3))
y = - 6x + (6 - 6 * sqrt(3))) + (- 3 + 6 * sqrt(3))
y = - 6x + 3
���Q�F
f(x) = - x�O4 �{ 4x^3 + 6x^2 - 4x
(1)
f'(x) = - 4x^3 + 12x^2 + 12x - 4
f(x) = (x/4 - 1/4)(- 4x^3 + 12x^2 + 12x - 4) + (6x^2 - 1)
�Ȃ̂ŁC�]��� 6x^2 - 1 �ł��B
(2)
f'(x) = - 4x^3 + 12x^2 + 12x - 4 = - 4(x^3 - 3x^2 - 3x + 1)
= - 4(x + 1)(x^2 - 4x + 1)
= - 4(x + 1)(x - (2 - sqrt(3)))(x - (2 + sqrt(3)))
�����ŁC
x < - 1 �ŁCf'(x) > 0�Cf(x) �͒P������
x = - 1 �ŁCf'(x) = 0�Cf(x) �͋ɑ�l 5
- 1 < x < 2 - sqrt(3) �ŁCf'(x) < 0�Cf(x) �͒P������
x = 2 - sqrt(3) �ŁCf'(x) = 0�Cf(x)
�͋ɏ��l 41 - 24 * sqrt(3)
2 - sqrt(3) < x < 2 + sqrt(3) �ŁCf'(x) > 0�Cf(x) �͒P������
x = 2 + sqrt(3) �ŁCf'(x) = 0�Cf(x)
�͋ɑ�l 41 + 24 * sqrt(3)
2 + sqrt(3) < x �ŁCf'(x) < 0�Cf(x) �͒P������
�Ȃ̂ŁCy = f(x) �́C
(-1, 5), (2 - sqrt(3), 41 - 24 * sqrt(3)), (2 + sqrt(3), 41 + 24 * sqrt(3))
�ŋɒl���Ƃ�܂��B�����ŁC���̂R�_��ʂ�������́Cy = ax^2 + bx + c �Ƃ�����
a(-1)^2 + b(-1) + c = 5
a(2 - sqrt(3))^2 + b(2 - sqrt(3)) + c = 41 - 24 * sqrt(3)
a(2 + sqrt(3))^2 + b(2 + sqrt(3)) + c = 41 + 24 * sqrt(3)
�v�Z����ƁC
a - b + c = 5
(7 - 4 * sqrt(3))a + (2 - sqrt(3))b + c = 41 - 24 * sqrt(3)
(7 + 4 * sqrt(3))a + (2 + sqrt(3))b + c = 41 + 24 * sqrt(3)
->
a - b + c = 5
7a + 2b + c = 41
(4 * sqrt(3))a + (sqrt(3))b = 24 * sqrt(3)
->
2a + b = 12
(4 * sqrt(3))a + (sqrt(3))b = 24 * sqrt(3)
->
(2 * sqrt(3))a = 12 * sqrt(3)
->
a = 6, b = 0, c = - 1
�܂�C
y = 6x^2 - 1
�ɂȂ�܂��B
���R�@
�m���ɁC���P�Ɩ��Q�ɂ����āC���ꂼ��C(1)��(2)�̓�������v���Ă��܂��B
����́C��ʂɁC���̂悤�ɂ��Ă����܂��B
���Cf(x) �� n ���̑������Ƃ��܂��B����ƁCf'(x) �� n-1 ���̑������ł��B
�����ŁCg(x) �� n-2 ���̑������Ƃ��āC
f(x) = (ax + b) * f'(x) + g(x)
�Ə����܂��B���̂Ƃ��Cg(x) �́Cf(x) �� f'(x) �Ŋ������]��ɂȂ�܂��B
���āCf(x) �� n-1 �̈قȂ�_ (pk,f(pk)), k = 1, 2, ..., n-1 �ŋɒl���Ƃ����Ƃ��܂��B
���̕K�v�\�������́C���炩�ɁCf'(pk) = 0, k = 1, 2, ..., n-1 �ł����āCpk ���݂��ɈقȂ邱�Ƃł��B
����ƁCk = 1, 2, ..., n-1 �ɑ���
f(pk) = (a * pk + b) * f'(pk) + g(pk) = g(pk)
����́Cn-2 ���̑������� y = g(x) ���Cn-1 �̈قȂ�_ (pk,f(pk)) ��ʂ邱�Ƃ������Ă��܂��B
�܂�C�]�� g(x) �́Cn-1 �̈قȂ�_ (pk,f(pk)), k = 1, 2, ..., n-1 ��ʂ� n-2 ���̑��������ɂȂ��Ă��܂��B
(�l�@)
������Ƃ��邳�����Ƃ������ƁCg(x) = ��[i=0,n-2]{ai
* x^i} �ɂ����āC
n-1 �� ai, i = 0, ..., n-2�C�Ɋւ���P���̘A��������
g(pk) = f(pk), k = 1, 2, ..., n-1
���C������̉��������Ƃ��ؖ�����K�v������܂��B
(���������Ƃ͗]�� g(x) �̑��݂ɂ���Ė��炩�ł����C����ȊO�ɂ��邩������܂���B)
����͑�w���x���ɂȂ��Ă��܂��̂ŏȗ����܂������C�P���̘A���������̈�ʘ_����Cn-2 = m �Ƃ�����
ai �̌W���̍s��̍s��
|p1^m p1^(m-1) ... p1^2 p1 1|
|p2^m p2^(m-1) ... p2^2 p2 1|
|...........................|
|pm^m pm^(m-1) ... pm^2 pm 1|
�� 0 �łȂ����肽����̉��������Ƃ������C����ɁC���̍s�́C�s�̐��������܂��g���ƁC
��[1<=i<j<=m](pi - pj)�@�܂�C1 <= i < j <= m �ƂȂ邷�ׂĂ� (pi - pj) �̐�
�ɓ��������Ƃ������Cpi not= pj �������̂ŁC0 �ɂ͂Ȃ�܂���B
�����ŁC�K���Cai, i = 0, 1, ..., n-2 ��������m�肵�C���ꂪ y = g(x) �ɂȂ邱�Ƃ͕ۏ���Ă��܂��B
(���z)
����Ӗ����炩�Ȗ��ł����C�ʔ�����肾�Ǝv���܂����B
NO2�u�l�c�����v 3/26 11��56����M
�X�V4/12
���P
(1) ��(��)�����R�|�R���Q�|�U���{�T����C
�@�@��'(��)���R���Q�|�U���|�U���R(���Q�|�Q���|�Q)
�@��(��)����'(��)���v�Z����ƁC
�@�@�@�@�@�@�@�@�@�@�P�^�R�@�|�P�^�R
�@�@�@�@�@�@�@�@�@���\�\�\�\�\�\�\�\�\�\�\�\�\
�@�@�R�@�|�U�@�|�U�j�P�@�@�@�|�R�@�@�@�|�U�@�T
�@�@�@�@�@�@�@�@�@�@�P�@�@�@�|�Q�@�@�@�|�Q
�@�@�@�@�@�@�@�@�@�@�\�\�\�\�\�\�\�\�\�\�\�\�\
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�|�P�@�@�@�|�S�@�T
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�|�P�@�@�@�@�Q�@�Q
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�\�\�\�\�\�\�\�\�\
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�|�U�@�R
�@�@����(��)����'(��)(���^�R�|�P�^�R)�|�U���{�R
�@�]��́|�U���{�R�ƂȂ�D
(2) ��'(��)���O�@�́@�����P�}��R
�ł���D�ɒl��^���邘�̒l�����C���i���P�}��R�j�Ƃ���ƁC
�@�@��'(��)����'(��)���O
�@�@����(��)���|�U���{�R�C��(��)���|�U���{�R
�@�̂ɋɒl�̓_(���C��(��))�C(���C��(��))�i�������j�����Ԓ����̕������́C
�@�@�����|�U���{�R
���Q
(1) ��(��)���|���S�{�S���R�{�U���Q�|�S������C
�@�@��'(��)���|�S���R�{�P�Q���Q�{�P�Q���|�S���|�S(���R�|�R���Q�|�R���{�P)
�@�@�@�@�@���|�S{(���R�{�P)�|�R��(���{�P)}���|�S(���{�P){(���Q�|���{�P)�|�R��}
�@�@�@�@�@���|�S(���{�P)(���Q�|�S���{�P)
�@��(��)����'(��)���v�Z����ƁC
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�P�^�S�@�|�P�^�S
�@�@�@�@�@�@�@�@�@�@�@�@�@���\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�@�@�|�S�@�P�Q�@�P�Q�@�|�S�j�|�P�@�@�S�@�@�@�@�@�U�@�|�S�@�@�O
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�|�P�@�@�R�@�@�@�@�@�R�@�|�P
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�P�@�@�@�@�@�R�@�|�R�@�@�O
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�P�@�@�@�@�|�R�@�|�R�@�@�P
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�\�\�\�\�\�\�\�\�\�\�\�\�\
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�U�@�@�O�@�|�P
�@�@����(��)����'(��)(���^�S�|�P�^�S)�{�U���Q�|�P
�@�]��͂U���Q�|�P�ƂȂ�D
(2) ��'(��)���O�@�́@�����|�P�C�Q�}��R
�ł���D�ɒl��^���邘�̒l�����C���C���i���|�P�C�Q�}��R�j�Ƃ���ƁC
�@�@��'(��)����'(��)����'(��)���O
�@�@����(��)���U���Q�|�P�C��(��)���U���Q�|�P�C��(��)���U���Q�|�P
�@�̂ɋɒl�̓_(���C��(��))�C(���C��(��))�C(���C��(��))�i���������������j�����ԕ������̕������́C
�@�@�����U���Q�|�P
���R
�@��L�̉������ɂ���āC(1)�C(2)�̓�����v���闝�R�͖��炩�ł��낤�D
NO3�ukashiwagi�v
4/01 22��01����M
�ukashiwagi�v 4/07 07��48����M �X�V4/12
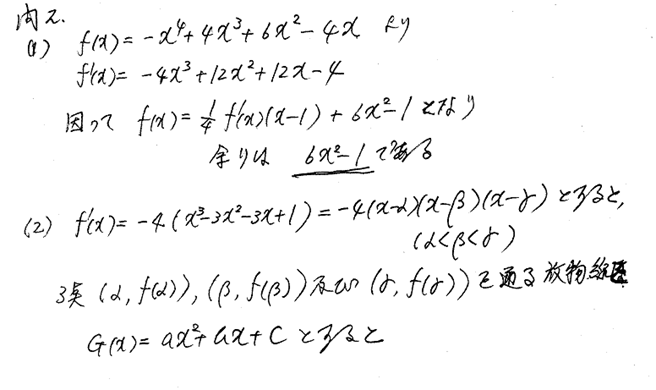
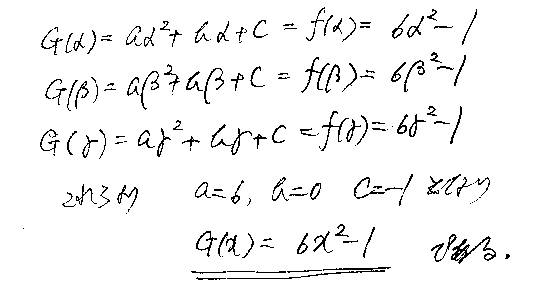
NO4�u�V�o�l�����v4/07 17��25����M
�X�V4/12

�F����A�������킩������A�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA
���[���ő����Ă��������B�҂��Ă��܂��B
![]()
