平成２２年９月５日

[流れ星]

　第２４５回数学的な応募問題解答ＮＯ２

　　　　　　＜解答募集期間：８月８日〜９月５日

［円に内接する三角形］

平成14年の京都大学入試問題を見ていると、次のような問題が出ていました。

問題：半径１の円周上に相異なる3点Ａ，Ｂ，Ｃがある。

（１）ＡＢ^２＋ＢＣ^２＋ＣＡ^２＞８ならば△ＡＢＣは鋭角三角形であることを示せ。

（２）ＡＢ^２＋ＢＣ^２＋ＣＡ^２≦９が成り立つことを示せ。また、この等号が成り立つのはどのような場合か。

ＮＯ５「浜田明巳」　08/26 15時58分受信 更新9/5

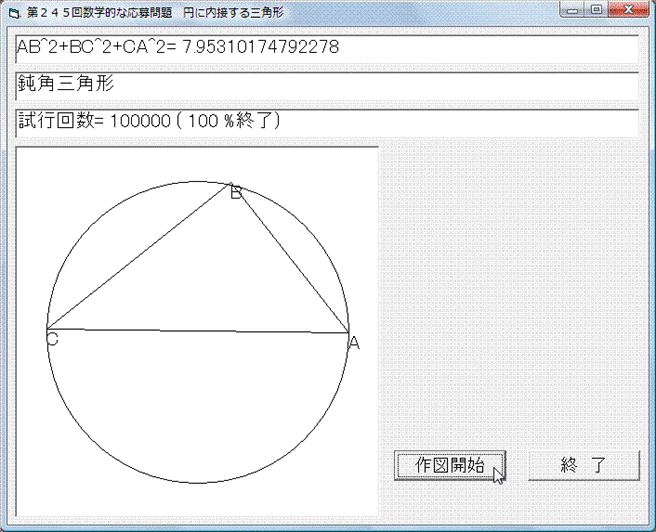
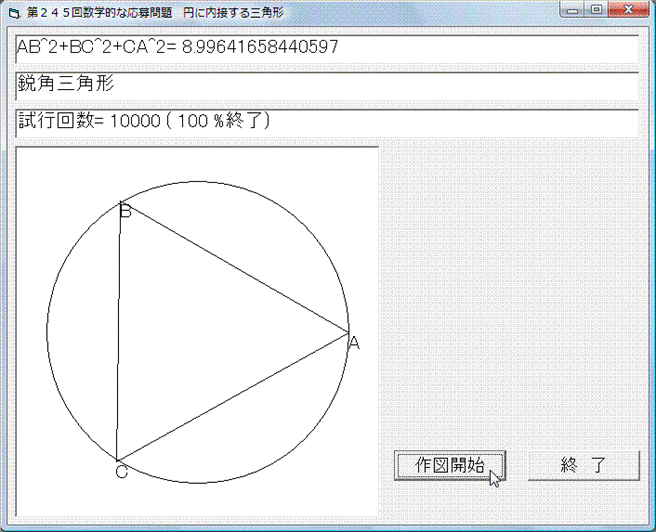
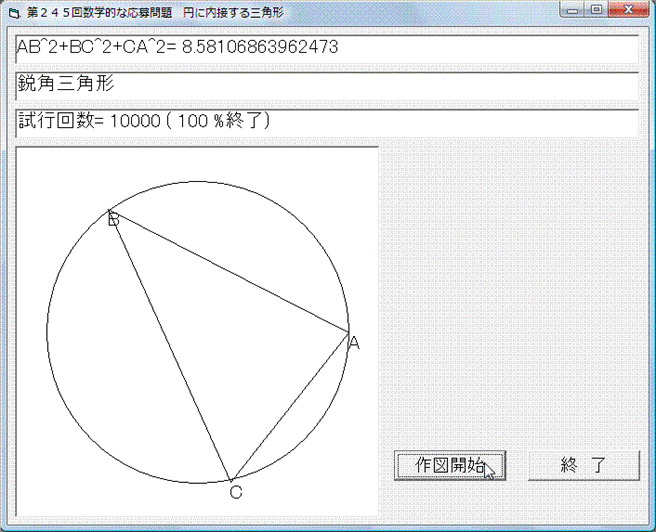
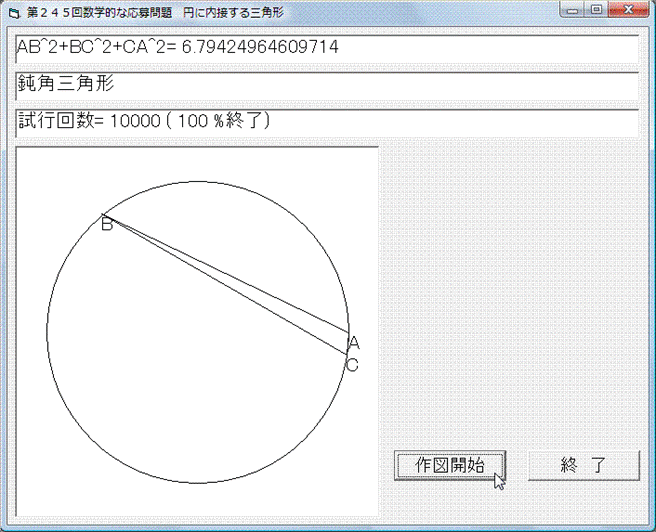
Visual Basic（バージョンは古いですが）で解いてみました．乱数を使って△ＡＢＣを描き，それぞれの場合において，ＡＢ2＋ＢＣ2＋ＣＡ2を計算して，

　　９より大きいとき，

　　８以下で鋭角三角形のとき，

強制的に終了するようにしています．

　何十回と走らせてみましたが，すべて滞りなく最後まで描き切りました．

Option Explicit
Const WAKU As Double = 1.2
Const dt_max As Double = 0.01 '偏角の動きの絶対値の最大値
Sub Form_Load()
    Picture1.BackColor = vbWhite
    Picture1.Scale (-WAKU, WAKU)-(WAKU, -WAKU)
    Picture2.BackColor = vbWhite
    Picture3.BackColor = vbWhite
    Picture4.BackColor = vbWhite
End Sub
Sub Command1_Click()
    Randomize Timer '乱数の初期化
    Dim Ax As Double
    Dim Ay As Double
    Dim At As Double '点Aの偏角
    Dim Bx As Double
    Dim By As Double
    Dim Bt As Double '点Bの偏角
    Dim Cx As Double
    Dim Cy As Double
    Dim Ct As Double '点Cの偏角
    Dim dBt As Double '点Bの偏角の動き
    Dim dCt As Double '点Cの偏角の動き
    Dim AB As Double
    Dim BC As Double
    Dim CA As Double
    Dim wa As Double 'AB^2+BC^2+CA^2
    Dim max_naikaku As Double '最大内角
    Dim shikoukaisuu As Long '試行回数
    Dim kaisuu As Long
    Dim owari As Integer
    Picture1.Cls
    Picture2.Cls
    Picture3.Cls
    Picture4.Cls
    At = 0 '点Aは固定
    Ax = Cos(At)
    Ay = Sin(At)
    Do
      shikoukaisuu = InputBox("試行回数=", "回数入力", 10000)
    Loop Until shikoukaisuu > 0
    owari = 0
    kaisuu = 1
    While owari = 0 And kaisuu <= shikoukaisuu
      If kaisuu = 1 Then '最初の点B,Cの決定
        Bt = 2 * pi() * Rnd
        Ct = 2 * pi() * Rnd
        dBt = 0
        dCt = 0
      Else
        dBt = dBt + dt_max * (Rnd * 2 - 1)
        If Abs(dBt) > dt_max Then
          dBt = 0
        End If
        Bt = Bt + dBt
        If Bt < 0 Then
          Bt = Bt + 2 * pi()
        ElseIf Bt > 2 * pi() Then
          Bt = Bt - 2 * pi()
        End If
        dCt = dCt + dt_max * (Rnd * 2 - 1)
        If Abs(dCt) > dt_max Then
          dCt = 0
        End If
        Ct = Ct + dCt
        If Ct < 0 Then
          Ct = Ct + 2 * pi()
        ElseIf Ct > 2 * pi() Then
          Ct = Ct - 2 * pi()
        End If
      End If
      Bx = Cos(Bt)
      By = Sin(Bt)
      Cx = Cos(Ct)
      Cy = Sin(Ct)
      AB = Sqr((Bx - Ax) * (Bx - Ax) + (By - Ay) * (By - Ay))
      BC = Sqr((Cx - Bx) * (Cx - Bx) + (Cy - By) * (Cy - By))
      CA = Sqr((Ax - Cx) * (Ax - Cx) + (Ay - Cy) * (Ay - Cy))
      wa = AB * AB + BC * BC + CA * CA
      Picture2.Cls
      Picture2.Print "AB^2+BC^2+CA^2="; wa
      If wa > 9 Then
        owari = 1
      End If
      If AB >= BC And AB >= CA Then
        max_naikaku = kaku(BC, CA, AB)
      ElseIf BC >= CA And BC >= AB Then
        max_naikaku = kaku(CA, AB, BC)
      Else
        max_naikaku = kaku(AB, BC, CA)
      End If
      Picture3.Cls
      If max_naikaku < pi() * 0.5 Then
        Picture3.Print "鋭角三角形"
      ElseIf max_naikaku = pi() * 0.5 Then
        Picture3.Print "直角三角形"
      Else
        Picture3.Print "鈍角三角形"
      End If
      If max_naikaku < pi() * 0.5 And wa <= 8 Then
        owari = 1
      End If
      Picture4.Cls
      Picture4.Print "試行回数="; shikoukaisuu; "("; kaisuu / shikoukaisuu * 100; "%終了)"
      Picture1.Cls
      Picture1.Circle (0, 0), 1, vbBlack
      Picture1.Line (Ax, Ay)-(Bx, By), vbBlack
      Picture1.Line -(Cx, Cy), vbBlack
      Picture1.Line -(Ax, Ay), vbBlack
      Picture1.CurrentX = Ax
      Picture1.CurrentY = Ay
      Picture1.Print "A"
      Picture1.CurrentX = Bx
      Picture1.CurrentY = By
      Picture1.Print "B"
      Picture1.CurrentX = Cx
      Picture1.CurrentY = Cy
      Picture1.Print "C"
      kaisuu = kaisuu + 1
    Wend
End Sub
Sub Command2_Click()
    Unload Me
End Sub
Private Function pi() As Double
    pi = 4 * Atn(1)
End Function
Private Function kaku(ByVal a As Double, ByVal b As Double, ByVal c As Double) As Double
    Dim cos_t As Double
    cos_t = (a * a + b * b - c * c) / (2 * a * b)
    kaku = Atn(Sqr(1 / cos_t / cos_t - 1))
    If cos_t < 0 Then
      kaku = pi() - kaku
    End If
End Function

ＮＯ６「ＭＶＨ」 　 08/31 15時25分受信 更新9/5

皆さん、答えがわかったら、一部でも構いませんから、解答とペンネームを添えて、
メールで送ってください。待っています。