平成２３年４月２４日

[流れ星]

　　　　　第２５６回数学的な応募問題解答

　　　　　　＜解答募集期間：4月3日〜4月24日

［屋根型の体積］

1997年の青山学院高等部の問題を改題して出題します。

1辺が６ｃｍの正四面体Ａ−ＢＣＤがあり、辺ＡＢ，ＡＣ，ＤＢ，ＤＣを１：２に内分する点をそれぞれＥ，Ｆ，Ｐ，Ｑとおく。面ＥＦＱＰで切り取られる頂点Ａを含む側の部分の体積を求めよ。ちなみに、ＥＦ，ＰＱを通り、面ＥＰＱＦと垂直な面がＡＤと交わる点をそれぞれＧ，Ｒとします。

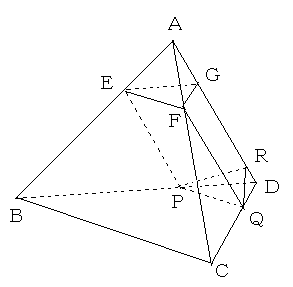
また、一般に正四面体Ａ−ＢＣＤの体積をＶとし、辺ＡＢ，ＡＣ，ＤＢ，ＤＣを１：（ｘ−１）に内分する点をそれぞれＥ，Ｆ，Ｐ，Ｑとおき、面ＥＦＱＰで切り取られる頂点Ａを含む側の部分の体積をＴとしたとき、Ｖ：Ｔの比をｘで表せ。

NO1「uchinyan」 04/03 13時53分受信

「uchinyan」 04/04 13時37分受信 更新4/24

第２５６回数学的な応募問題

［屋根型の体積］

どうせなので，一般的な場合から解いてしまいましょう。

正四面体の一辺の長さを a とします。また，x >= 1 とします。

まず，相似と △AEF，△DPQ は正三角形より，AE = AF = EF = DP = DQ = PQ = a/x です。

また，AD//EP，AD//FQ なので AD//平面EPQF で，平面EPQF⊥△GEF，平面EPQF⊥△RPQ より，

AD⊥△GEF，AD⊥△RPQ，AD⊥GF，AD⊥RQ になり，FQ⊥GF，FQ⊥RQ にもなります。

さらに，対称性より，GE = GF = RQ = RP，AG = DR です。そこで，∠FAG = 60°も使って，

AG = AF/2 = a/2x = DR，GR = a(x - 1)/x，GE = GF = √3/2 * a/x = RQ = RP

ここで，A から EF に垂線を下ろしその足を H とすると，EH = FH = a/2x なので，

三平方の定理を使って，AH = √2/2 * a/x になり，

△GEF = EF * AH * 1/2 = a/x * √2/2 * a/x * 1/2 = √2/4 * (a/x)^2 = △RPQ

そこで，

T = 三角すいA-EFG + 三角柱EFQ-PQR + 三角すいD-PQR

= △GEF * AG * 1/3 + △GEF * GR + △GEF * DR * 1/3

= △GEF * (AG + 3 * GR + DR)/3 = △GEF * (AD + 2 * GR)/3

= √2/4 * (a/x)^2 * (a + 2 * a(x - 1)/x)/3

= √2/12 * a^3 * (3x - 2)/x^3

一方で，V は，A から △BCD に下ろした垂線の足を I とすると，三平方の定理などより，

△BCD = √3/4 * a^2，AI = √6/3 * a，V = △BCD * AI * 1/3 = √2/12 * a^3

なので，

V：T = 1：(3x - 2)/x^3 = x^3：(3x - 2)

になります。また，最初の問題は，a = 6 cm，x = 3 なので，

T = √2/12 * 6^3 * (3 * 3 - 2)/3^3 = 14√2/3 cm^3

になります。

(別解)

まず最初に，一般に，

△ABC の頂点 A，B，C からそれぞれ垂線を立てて，AD = a，BE = b，CF = c としたときの

三角柱を切断したような 立体ABC-DEF の体積を考えます。ただし，a <= b <= c とします。

D を通って △ABC に平行な平面を考え，BE，CF との交点を P，Q とし，

△DPQ の PQ を底辺としたときの高さを h，△ABC の面積を S すると，

△DPQ = PQ * h * 1/2，△DPQ ≡ △ABC，△DPQ = △ABC = S に注意して，

立体ABC-DEF = 四角すいD-PQFE + 三角柱ABC-DPQ

= □PQFE * h * 1/3 + △ABC * a

= ((PE + QF) * PQ * 1/2) * h * 1/3 + △ABC * a

= ((b - a) + (c - a))/3 * △ABC + △ABC * a

= (a + b + c)/3 * S

になります。

さて，この問題に戻って，正四面体の一辺の長さを d とします。また，x >= 1 とします。

さらに，B，C を通り AD に垂直な平面を考え，AD，EP，FQ との交点を M，K，L とします。

対称性より AM = DM = d/2 で，AD//EP，AD//FQ より AD//平面EPQF，△MKL⊥平面EPQF です。

そこで，立体MKL-AEF = 立体MKL-DPQ に先ほどの式が使えます。

相似，正四面体の面は正三角形，□EPQF は平行四辺形，EF//KL//PQ などより，

AE = AF = EF = DP = DQ = PQ = KL = d/x，EP = FQ = d(x - 1)/x，MK = ML = √3/2 * d/x です。

また，M から KL に垂線を下ろしその足を N とすると，KN = LN = d/2x なので，

三平方の定理を使って，MN = √2/2 * d/x になり，

△MKL = KL * MN * 1/2 = d/x * √2/2 * d/x * 1/2 = √2/4 * (d/x)^2 = S

a = AM = DM = d/2，b = c = EP/2 = FQ/2 = d(x - 1)/2x

T = 立体MKL-AEF + 立体MKL-DPQ = 立体MKL-AEF * 2 = (a + b + c)/3 * S * 2

= (d/2 + d(x - 1)/2x * 2)/3 * √2/4 * (d/x)^2 * 2

= √2/12 * d^3 * (3x - 2)/x^3

後は，d -> a として，同じです。

(感想)

相似と三平方の定理だけでできたので，これって高校入試レベルかな？，と思ったら，

「高等部」と書いてありましたね (^^;

V：T = 1：(3x - 2)/x^3 = x^3：(3x - 2) は，

x -> 1 で V：T -> 1：1，x = 2 で V：T = 2：1，x -> ∞ で V：T -> 1：0，

となって，直感とも一致します。

なお，(別解)の三角柱を切断したような立体は，あまり言葉はよくないのですが，

受験算数？では，断頭三角柱と言うそうで，公式としてよく使われているようです。

(底面積)×(高さの平均)，と直感的にも分かりやすく，それなりに便利な公式で，

覚えておいても損はないと思います。

＜水の流れ：よくご存知ですね。したがって、この問題にあてはめると、三角形EFGの面積をSとして、AD＝a、FQ＝ｂ、EP＝ｃとすると、求める体積VはS（a＋ｂ＋ｃ）÷３　で出てきます。この場合はS＝√２、a＝６、ｂ＝４、ｃ＝４ですから

S＝√２（６＋４＋４）÷３＝１４√２／３　　答　＞

NO2「ｽﾓｰｸﾏﾝ」 04/18 02時43分受信 更新4/24

一般化した方を先に考えると...図から...
Aを含む方の体積は...
上の相似な三角錐の体積+三角柱の傾いた体積＝(1/x)^3+(1/x)^2*{(x-1)/x}
　　　　　　　　　　　　　　　　　　＝x/x^3

＝1/x^2
つまり...　V ：T ＝ x^2 ：1

辺が6 cmの正四角錐の x=3 の場合を考えればいいので...
正四角錐の体積=(6*3√3/2)*(√{6^2-(2√3)^2})*(1/3)
                       =18√2
なので...　求める体積 T=(1/9)*18√2
                   =2√2 cm^3

＜水の流れ：そううまくなっていないと思っています＞

NO3「MVH」 04/22 00時03分受信 更新4/24