平成２６年６月２９日

[流れ星]

　　　　　第308回数学的な応募問題

　　　　　　＜解答募集期間：6月29日〜7月20日＞

［特殊な証明］

問題：△ＡＢＣは∠Ａ＝６０°の三角形とする。∠Ｂ,∠Ｃの二等分線となるように辺ＡＣ,ＡＢ上に点Ｄ，Ｅをとる。さらに、ＢＤ＝ＢＦ，ＣＥ＝ＣＧとなるような点Ｆ，Ｇが辺ＡＢ，ＡＣ上にそれぞれ存在するものとする。このとき、ＦＧ‖ＢＣを証明せよ。

NO1「uchinyan」 　　　 06/29 12時38分　受信

「uchinyan」 　　　 06/20 12時10分　受信 更新 07/20

(解法1)　より図形的な解法

BD と CE の交点を P とします。

∠ABC + ∠ACB = 180°- ∠BAC = 180°- 60°= 120°

∠ABP + ∠ACP = ∠PBC + ∠PCB = (∠ABC + ∠ACB)/2 = 120°/2 = 60°

∠EPB = ∠DPC = ∠PBC + ∠PCB= 60°

∠DPE = ∠BPC = 180°- ∠EPB = 180°- 60°= 120°

そこで，□AEPD は円に内接します。∠PDC = ∠PEB = ∠BAC= 60°もいえます。

＜「早起きのおじさん」からご指摘を受けた部分に下線を引きました。7月25日記入＞

また，P は，∠ABC の二等分線と ∠ACB の二等分線の交点なので，△ABC の内心で，

AP は ∠BAC の二等分線，∠BAP = ∠CAP = ∠BAC/2 = 60°/2 = 30°

これより，弧PE = 弧PD，PE = PD，です。

そこで，∠PDC = ∠PEB にも注意して，

△PDC を P を中心に反時計回りに回転し PD を PE に重ね，C の移動先を C' とすると，

D と E は一致し，B，E，C' は同一直線上にあり，△PBC' ができ，

さらに，∠BPE = 60°= ∠CPD = ∠C'PE，つまり，PE は ∠BPC' の二等分線，になります。

そこで，PB：PC = PB：PC' = BE：C'E = BE：CD，BP：BE = CP：CD，がいえます。

一方で，∠BAD = 60°= ∠BPE，∠CAE = 60°= ∠CPD，なので，

△ABD ∽ △PBE，△ACE ∽ △PCD，BA：BD = BP：BE = CP：CD = CA：CE，となります。

そこで，BF = BD，CG = CE，を使って，

BA：BF = BA：BD = CA：CE = CA：CG，AF：AB = AG：AC，△AFG ∽ △ABC，∠AFG = ∠ABC

となって，FG//BC，がいえます。

(解法2)　計算主体の解法

BC = a，CA = b，AB = c，BF = BD = d，CG = CE = e，とします。

FG//BC は，∠AFG = ∠ABC，△AFG ∽ △ABC，AF：AB = AG：AC，FB：AB = GC：AC，と同値なので，

d/c = e/b，を示せばよく，さらにこれは，d^2/c^2 - e^2/b^2 = 0，と同値なので，以下ではこれを示します。

まず，B から AC に垂線を下ろしその足を H とすると，∠A = 60°より，AH = c/2，BH = (√3/2)c，で，

三平方の定理より，a^2 = (b - c/2)^2 + ((√3/2)c)^2 = b^2 + c^2 - bc，です。

次に，BD は ∠B の二等分線，CE は ∠C の二等分線，なので，

AD：CD = BA：BC = c：a，AD = bc/(a + c)，AE：BE = CA：CB = b：a，AE = bc/(a + b)

さらに，∠A = 60°なので，先ほどと同様に三平方の定理を使って，

d^2 = c^2 + (bc/(a + c))^2 - bc^2/(a + c)，e^2 = b^2 + (bc/(a + b))^2 - cb^2/(a + b)

そこで，

d^2/c^2 - e^2/b^2

= (1 + b^2/(a + c)^2 - b/(a + c)) - (1 + c^2/(a + b)^2 - c/(a + b))

= (b^2(a + b)^2 - b(a + b)^2(a + c) - c^2(a + c)^2 + c(a + b)(a + c)^2)/((a + b)(a + c))^2

= ((b(a + b) + c(a + c))(b(a + b) - c(a + c)) - (a + b)(a + c)(b(a + b) - c(a + c)))/((a + b)(a + c))^2

= (b(a + b) + c(a + c) - (a + b)(a + c))(b(a + b) - c(a + c))/((a + b)(a + c))^2

= (b^2 + c^2 - bc - a^2)(a + b + c)(b - c)/((a + b)(a + c))^2

ここで，a^2 = b^2 + c^2 - bc だったので，

d^2/c^2 - e^2/b^2 = 0

つまり，FG//BC，になります。

(考察)

∠A が 60°でない一般の場合には，(解法2)で余弦定理を用いて，

a^2 = b^2 + c^2 - (2cosA)bc

d^2 = c^2 + (bc/(a + c))^2 - (2cosA)(bc^2/(a + c))

e^2 = b^2 + (bc/(a + b))^2 - (2cosA)(cb^2/(a + b))

d^2/c^2 - e^2/b^2

= (1 + b^2/(a + c)^2 - (2cosA)(b/(a + c))) - (1 + c^2/(a + b)^2 - (2cosA)(cb^2/(a + b)))

= (b^2(a + b)^2 - (2cosA)b(a + b)^2(a + c) - c^2(a + c)^2 + (2cosA)c(a + b)(a + c)^2)/((a + b)(a + c))^2

= ((b(a + b) + c(a + c))(b(a + b) - c(a + c)) - (2cosA)(a + b)(a + c)(b(a + b) - c(a + c)))/((a + b)(a + c))^2

= (b(a + b) + c(a + c) - (2cosA)(a + b)(a + c))(b(a + b) - c(a + c))/((a + b)(a + c))^2

= ((b^2 + c^2 - (2cosA)bc - (2cosA)a^2) + (1 - 2cosA)a(b + c))(a + b + c)(b - c)/((a + b)(a + c))^2

= ((1 - 2cosA)a^2 + (1 - 2cosA)a(b + c))(a + b + c)(b - c)/((a + b)(a + c))^2

= (1 - 2cosA)a(b - c)(a + b + c)^2/((a + b)(a + c))^2

となります。

これが 0 になる，つまり，FG//BC，となるのは，

cosA = 1/2，つまり，∠A = 60°，又は，b = c，つまり，AB = AC の二等辺三角形

だけのようですね。

(感想)

問題を見てすぐに思ったのは，AB = AC の二等辺三角形ならば ∠A に関わらず成立する，ということで，

実は，最初の解法は(考察)の一般の角度もにらんだもので，三角関数で解いたものでした。

それでも思ったよりもあっさりと解けてしまいました。(解法2)はこれを ∠A = 60°に特殊化したものです。

その後，多分，もっと図形的にも解けるだろう，と思って考えたのが(解法1)です。

いろいろな解法がありそうですね。

「uchinyan」 　　　 07/25 11時47分　受信 更新 07/25

＜コメント：「∠PDC = ∠PEB = ∠BAC= 60°」 は，∠PDC = ∠PEA

の書き間違いです。これで以降は問題ないと思います。なお，∠PDC = ∠PEA を使わなくても済む，若干の別解を追加しました。＞

(解法1)　より図形的な解法

BD と CE の交点を P とします。

∠ABC + ∠ACB = 180°- ∠BAC = 180°- 60°= 120°

∠ABP + ∠ACP = ∠PBC + ∠PCB = (∠ABC + ∠ACB)/2 = 120°/2 = 60°

∠EPB = ∠DPC = ∠PBC + ∠PCB = 60°

∠DPE = ∠BPC = 180°- ∠EPB = 180°- 60°= 120°

そこで，□AEPD は円に内接します。また，∠PDC = ∠PEA がいえます。

また，P は，∠ABC の二等分線と ∠ACB の二等分線の交点なので，△ABC の内心で，

AP は ∠BAC の二等分線，∠BAP = ∠CAP = ∠BAC/2 = 60°/2 = 30°

これより，弧PE = 弧PD，PE = PD，です。

そこで，∠PDC = ∠PEA にも注意して，

△PDC を P を中心に反時計回りに回転し PD を PE に重ね，C の移動先を C' とすると，

D と E は一致し，B，E，C' は同一直線上にあり，△PBC' ができ，

さらに，∠BPE = 60°= ∠CPD = ∠C'PE，つまり，PE は ∠BPC' の二等分線，になります。

そこで，PB：PC = PB：PC' = BE：C'E = BE：CD，BP：BE = CP：CD，がいえます。

一方で，∠BAD = 60°= ∠BPE，∠CAE = 60°= ∠CPD，なので，

△ABD ∽ △PBE，△ACE ∽ △PCD，BA：BD = BP：BE = CP：CD = CA：CE，となります。

そこで，BF = BD，CG = CE，を使って，

BA：BF = BA：BD = CA：CE = CA：CG，AF：AB = AG：AC，△AFG ∽ △ABC，∠AFG = ∠ABC

となって，FG//BC，がいえます。

(若干の別解)

弧PE = 弧PD，PE = PD，までは(解法1)と同じ。

ここで，△PBE を PB に関して，△PDC を PC に関して，それぞれ折り返すと，

PE = PD なので折り返した E と D は一致します。これを，Q とします。

また，∠PBE = ∠PBC，∠PCD = ∠PCB なので Q は BC 上にあります。

さらに，∠BPE = 60°= ∠CPD なので，△PBE と △PDC を折り返したものは △PBC になります。

(∠PDC = ∠PEA より，∠PQB + ∠PQC = ∠PEB + ∠PDC = ∠PEB + ∠PEA = 180°もいえます。

これは，△PBE と △PDC を折り返したものが △PBC になることの更なる根拠ですが，

この解法では，これは，したがって，∠PDC = ∠PEA は，特に必要ありません。)

このとき，∠BPQ = ∠BPE = 60°= ∠CPD = ∠CPQ なので，PQ は ∠BPC の二等分線，になります。

そこで，PB：PC = BQ：CQ = BE：CD，BP：BE = CP：CD，がいえます。

後は，(解法1)と同じです。

(解法2)　計算主体の解法

BC = a，CA = b，AB = c，BF = BD = d，CG = CE = e，とします。

FG//BC は，∠AFG = ∠ABC，△AFG ∽ △ABC，AF：AB = AG：AC，FB：AB = GC：AC，と同値なので，

d/c = e/b，を示せばよく，さらにこれは，d^2/c^2 - e^2/b^2 = 0，と同値なので，以下ではこれを示します。

まず，B から AC に垂線を下ろしその足を H とすると，∠A = 60°より，AH = c/2，BH = (√3/2)c，で，

三平方の定理より，a^2 = (b - c/2)^2 + ((√3/2)c)^2 = b^2 + c^2 - bc，です。

次に，BD は ∠B の二等分線，CE は ∠C の二等分線，なので，

AD：CD = BA：BC = c：a，AD = bc/(a + c)，AE：BE = CA：CB = b：a，AE = bc/(a + b)

さらに，∠A = 60°なので，先ほどと同様に三平方の定理を使って，

d^2 = c^2 + (bc/(a + c))^2 - bc^2/(a + c)，e^2 = b^2 + (bc/(a + b))^2 - cb^2/(a + b)

そこで，

d^2/c^2 - e^2/b^2

= (1 + b^2/(a + c)^2 - b/(a + c)) - (1 + c^2/(a + b)^2 - c/(a + b))

= (b^2(a + b)^2 - b(a + b)^2(a + c) - c^2(a + c)^2 + c(a + b)(a + c)^2)/((a + b)(a + c))^2

= ((b(a + b) + c(a + c))(b(a + b) - c(a + c)) - (a + b)(a + c)(b(a + b) - c(a + c)))/((a + b)(a + c))^2

= (b(a + b) + c(a + c) - (a + b)(a + c))(b(a + b) - c(a + c))/((a + b)(a + c))^2

= (b^2 + c^2 - bc - a^2)(a + b + c)(b - c)/((a + b)(a + c))^2

ここで，a^2 = b^2 + c^2 - bc だったので，

d^2/c^2 - e^2/b^2 = 0

つまり，FG//BC，になります。

(考察)

∠A が 60°でない一般の場合には，(解法2)で余弦定理を用いて，

a^2 = b^2 + c^2 - (2cosA)bc

d^2 = c^2 + (bc/(a + c))^2 - (2cosA)(bc^2/(a + c))

e^2 = b^2 + (bc/(a + b))^2 - (2cosA)(cb^2/(a + b))

d^2/c^2 - e^2/b^2

= (1 + b^2/(a + c)^2 - (2cosA)(b/(a + c))) - (1 + c^2/(a + b)^2 - (2cosA)(cb^2/(a + b)))

= (b^2(a + b)^2 - (2cosA)b(a + b)^2(a + c) - c^2(a + c)^2 + (2cosA)c(a + b)(a + c)^2)/((a + b)(a + c))^2

= ((b(a + b) + c(a + c))(b(a + b) - c(a + c)) - (2cosA)(a + b)(a + c)(b(a + b) - c(a + c)))/((a + b)(a + c))^2

= (b(a + b) + c(a + c) - (2cosA)(a + b)(a + c))(b(a + b) - c(a + c))/((a + b)(a + c))^2

= ((b^2 + c^2 - (2cosA)bc - (2cosA)a^2) + (1 - 2cosA)a(b + c))(a + b + c)(b - c)/((a + b)(a + c))^2

= ((1 - 2cosA)a^2 + (1 - 2cosA)a(b + c))(a + b + c)(b - c)/((a + b)(a + c))^2

= (1 - 2cosA)a(b - c)(a + b + c)^2/((a + b)(a + c))^2

となります。

これが 0 になる，つまり，FG//BC，となるのは，

cosA = 1/2，つまり，∠A = 60°，又は，b = c，つまり，AB = AC の二等辺三角形

だけのようですね。

(感想)

問題を見てすぐに思ったのは，AB = AC の二等辺三角形ならば ∠A に関わらず成立する，ということで，実は，最初の解法は(考察)の一般の角度もにらんだもので，三角関数で解いたものでした。それでも思ったよりもあっさりと解けてしまいました。(解法2)はこれを ∠A = 60°に特殊化したものです。その後，多分，もっと図形的にも解けるだろう，と思って考えたのが(解法1)です。いろいろな解法がありそうですね。

NO2「早起きのおじさん」 07/05 23時02分　受信 更新 07/20

308解答　早起きのおじさん

●方針

FGとBCが平行であることをいうために、AB：AC＝AF：AGを示します。

特別な閃きや冴えがなくてもよいように計算でやります。

△ABCにおいて、BC=a、CA=b、AB＝c、BD＝x、CE＝y、∠ABC＝2α、∠BCA＝2βとおきます。

●準備

○△ABCの面積Sを利用して、x、yについて調べます。

角αを用いて面積の計算をし、xを求めます。

BDで2つの三角形に分かれているので、

角βを用いて面積の計算をし、yを求めます。

CEで2つの三角形に分かれているので、

○αとβの関係を調べます。

∠A＝60°なので、2α＋2β＝120°だから、α＋β＝60°

○正弦定理を用いて辺の値を角αで表します

だから、

●AF：AGを調べます。

この比がc：bになればよいので、上の式のカッコの中の赤い部分が互いに等しければ良いことになります。

だから、この部分の比の値を調べて1かどうかを見てみます。

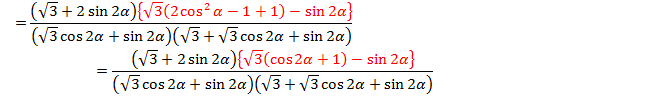
よって成立します。

■おまけ

今回の問題のタイトルに特殊な証明とあります。

はじめは、変わった証明方法をするのかと思いました。

しかし、解いて行くうちにこの問題はA＝60°のときだけ成立すると気づきました。

■一般的に考えてみると、

○正弦定理を用いて辺の値を角αで表します。

だから、

■AF：AGを調べます。

この比がc：bになればよいので、上の式のカッコの中の赤い部分が互いに等しければ良いことになります。

だから、この部分の比の値を調べて1かどうかを見てみます。

A＝60°のときは、分子、分母をそれぞれ展開して同じ式になりました。

Aが固定されているとき、和が一定という制約でαとβが変化していくとき一般には等しくなりません。

考えられるのは、α＝βのときです。

つまり、A＋4α＝180°より、

この特別なときは、FGとBCが平行になります。

「早起きのおじさん」 07/17 21時23分　受信 更新 07/20

308解答＿２　早起きのおじさん

●方針

FGとBCが平行であることをいうために、FからBCまでの距離そしてGからBCまでの距離が等しいことを示します。

そのために をいいます。

△ABCにおいて、BC=a、CA=b、AB＝c、∠ABC＝2α、∠BCA＝2βとおきます。

●準備は前の解答と同じなので、

α＋β＝60°

● か調べます。

まず、

次に、

よって成立します。

308解答＿３

●方針

FGとBCが平行であることをいうために、GC：FB＝b：c をいいます。

△ABCにおいて、BC=a、CA=b、AB＝c、∠ABC＝2α、∠BCA＝2βとおきます。

●準備は前の解答と同じなので、

2α＋2β＝120°(α+β＝60°)

● GC：FB＝b：c か調べます。

よって成立します。

＜コメント：前の解答のときに幾何的な説明ができたらまた解答を送るといいましたが結局できませんでした。

内心のこと、メネラウスの定理を使うこと、BDとCEのなす角が60°のこと、二つの二等辺三角形BDFとCGEの頂点からの垂線が直交することなど考えてみましたが。

うまい補助線が見つかりませんでした。幾何的に考えるのは難しいです。

途中同じような解答ばかり作ったのですが送ります。計算でゴリゴリやるのはわりと得意です。

NO3「二度漬け白菜」 07/09 00時03分　受信 更新 07/20

(FG ‖ BC であることの証明)

まずはじめに，△ABC と △AFG が相似であることを示す．

線分BD と 線分CE との交点を I とする．
辺AB，BC，CA の長さをそれぞれ　AB=c，BC=1，CA=b とする．

CD：AD = BC：BA = 1：c であるから AD = (b*c)/(1+c)．
BE：AE = CB：CA = 1：b であるから AE = (c*b)/(1+b)．

4角形ADIE は円に内接する．
(∵ 4角形ADIEにおいて，∠EID = ∠BIC = 180°- (∠CBI+∠BCI) =
180°- (1/2)*(∠CBA+∠BCA) = 180°- (1/2)*(180°- ∠BAC) =
180°- (1/2)*(180°- 60°) = 120°． よって，∠EID + ∠DAE = (120+60)°= 180°)

また直線AIは∠BACの二等分線である．
( ∵点Iより辺AB，BC，CAに下ろした垂線の足をそれぞれP，Q，Rとする．
△IPBと△IQBにおいて，IB=IB，∠IBP=∠IBQ，∠IPB=∠IQB=90°．
斜辺と1鋭角が等しいので △IPB≡△IQB．よって，IP=IQ．
同様にして △IQC≡△IRC から IQ=IR が示せる．よって，IP=IQ=IR．
以上より △IAPと△IARにおいて，斜辺と他の1辺が等しいので，
△IAP≡△IAR．よって ∠IAP=∠IAR )
よって ∠IAD=∠IAE=30°．

以上のことから， ID=IE ．(円周角の大きさが等しいので弦の長さも等しい)
　　
ID=IE=s とおく．また IB=t，IC=u とおく．

△ABD ∽ △IBE である．
(∵∠ABD = ∠IBE，∠BIE = 180°- ∠BIC = (180-120)°= 60°= ∠BAD．)
よって，AB：AD = IB：IE　つまり，c：((b*c)/(1+c)) = t：s
よって，s = (t*b)/(1+c)．

△ACE ∽ △ICD である．
(∵∠ACE = ∠ICD，∠CID = 180°- ∠BIC = (180-120)°= 60°= ∠CAE．)
よって，AC：AE = IC：ID　つまり，b：((c*b)/(1+b)) = u：s ．
よって，u = ((1+b)/c)*s = ((1+b)/c)*((t*b)/(1+c)) = (t*b*(1+b))/(c*(1+c))．

さて，△ABCと△AFG において，
AB：AF = AB：(AB-BF) = AB：(AB-BD) = AB：(AB-(IB+ID))
= c：(c-(t+s)) = c：(c-(t+(t*b)/(1+c))) = c*(1+c)：(c*(1+c)-t*(1+b+c))．
また，AC：AG = AC：(AC-CG) = AC：(AC-CE) = AC：(AC-(IC+IE))
= b：(b-(u+s)) =  b：(b-((t*b*(1+b))/(c*(1+c))+(t*b)/(1+c)))
= b：(b-(b*t*(1+b+c)/(c*(1+c))))
= 1: (1-t*(1+b+c)/(c*(1+c)))
= c*(1+c)：(c*(1+c)-t*(1+b+c))．
よって，AB：AF = AC：AG = c*(1+c)：(c*(1+c)-t*(1+b+c))．
また，∠BAC=∠FAG=60°．
△ABCと△AFGは 対応する2組の辺の長さの比と挟まれる角の大きさが

それぞれ等しいので，△ABC ∽ △AFG である．

△ABC ∽ △AFG であるので，∠ABC = ∠AFG である．
つまり 直線BC と 直線FG はその同位角が等しい．
よって，FG ‖ BC である．(証明終)

今回の問題は解くのに苦労しました．
BC=1，∠ABD=θとし，さらに tan(θ/2) = t とおけば，
AB，AC，BF，CGの長さを t の式で表すことができます．
しかしこのやり方では 式がかなり複雑になってしまいます．
いろいろ悩んでようやく上記のような解法をみつけました．
ほぼ中学時代に学校で習った幾何の知識だけで解けてしまうのですね．
驚きました．