�ߘa�Q�N�S���P�Q��
 [���ꐯ]
[���ꐯ]
�@�@�@�@��384�����w�I�ȉ����
�@�@�@�@����W���ԁF3��15���`4��12����
�m��{���[�Z�z�P�n
�]�ˎ������̘a�Z�ƒJ���i1800�`1841�j�����܂����B恂͏��A�ʏ͎̂��Y���A���͎m�D�A���͗H�ցB��X���Z����_�鉺�ň���������ƂƂ��A�����͔Ŗ؉��A���͗ǔ��B�@�@�@
�ނ͘a�Z���_�˂̎�Ґ��얯����Ɋw�сA�����S���I�ɒ����Șa�Z�ƂŖ��É��̖k��ҌՂɒ�q��������Ă���B�܂��A�������_�Řa�Z�m���J���Z�@�E�Z�p�𑽂��l�ɋ����Ă���B����ɁA�a�Z�ƒJ�H�ւ͐��w�̖����Z�z�Ƃ��Đ_�Г��Ɍf���Ă���B����Ɂu�ԏp�V�Ӂv�u�H�֎Z�ҁv�Ȃǂ�����B�ނ�1841�N�ɖS���Ȃ����Ƃ���킪���Z����{��Ђ�1842�N�Z�z12����c���܂����B�ł��A�c�O�Ȃ���Z�z�͌������Ă��܂���B�����ŁA�F����̗͂���ŁA��@������ɓ`�������A�o�肵�܂����B
�@��384��3���܂��B
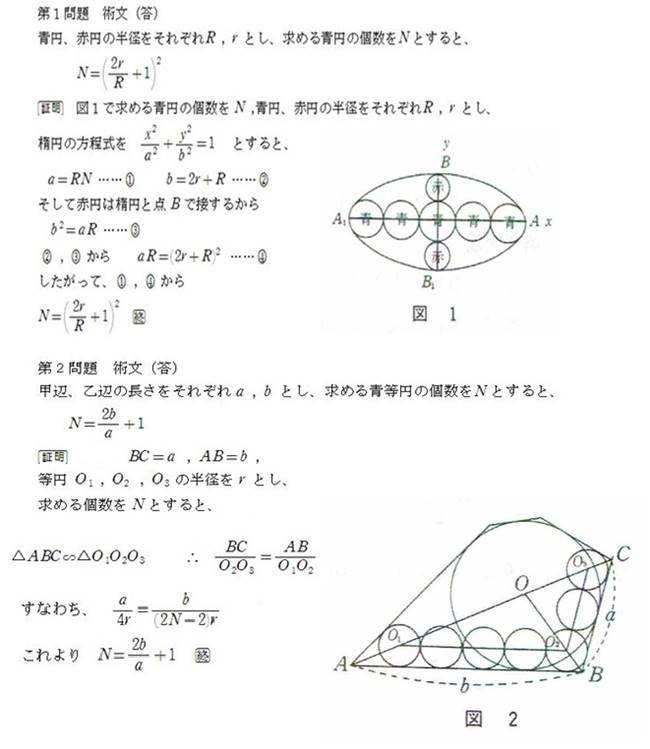
��P���@�ȉ~���ɐԉ~��ƍł������̐��~������B�ԉ~�Q�Ɛ~��Ƃ̒��a�̘a�͒Z�a�ɓ������B�~�O���珉�߂Ē��������𑝂��Ƃ���B�ԉ~�a�Ɛ~�a�����ꂼ��m���Đ��~�̌������߂�B
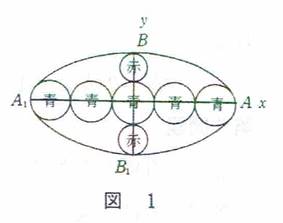
��Q���@���p�`�i�Ӑ��͖��W�A�����ʼn��Ɍ܊p�`�Ƃ���j�̓��ԉ~������B�݂��ɊO�ڂ���R�̐~�͍b�ӂɐڂ��A���ӂɐڂ���悤�ɐ��~�����݂��ɊO�ڂ�����B�b�ӁA���ӂ̒��������ꂼ��m���Đ��~�̌������߂�B

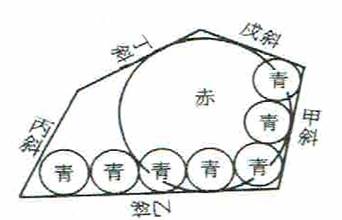
�Q�l�}
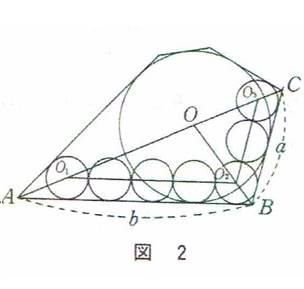
��R���@��ʓ��ɒ������������~��A�~��i���~�̒��a�̂S���R��~�̒��a�Ƃ���j�Ɛԉ~�i���~�j���i���Ɏ��j������B�~�A�ԉ~�̒��a��m���Đԓ��~�̌������߂�B

�Q�l�}
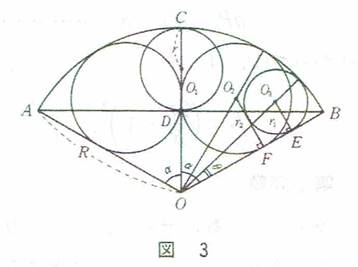
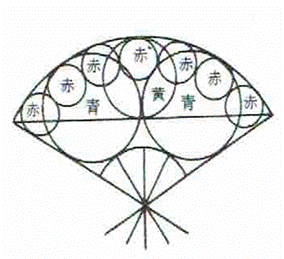
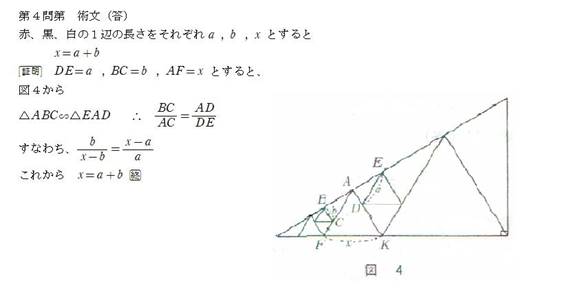
��S���@���p�O�p�`�̓��ցA�قȂ�܌̐��O�p�`������B�ԁA���̈�ӂ̒��������ꂼ��m���Ĕ��̈�ӂ̒��������߂�

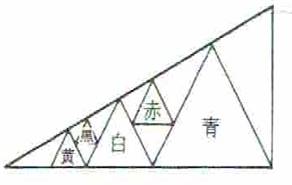
�Q�l�}
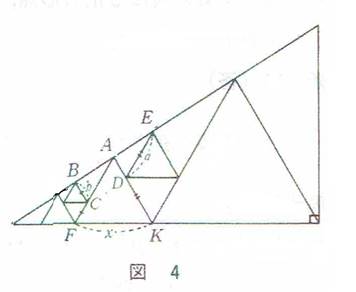
�o�T�@���̎Z�z�̉���@���؏d�V�@���@����o�Ł@
�@
�lj����@�o��ҁu�W���[�J�[�v

�����̗���F�Y��ȎZ�z���̖��ł���
NO1�u�W���[�J�[�v �@
03/26 09��16���@��M �X�V 4/12
��S����͒��w�����x�������B
�����̗���F�o��҂͓���12�̏��N�ł��B��
�i�ؖ��j�Q�l�}�ŁC��ABC�䁢EAD���C
b:(x-a)=(x-b):a
(x-a)(x-b)=ab
x>0���Cx=a+b�@�i�I�j
NO�Q�u���N���̂�������v 03/30 17��43���@��M �X�V 4/12
���1
���̖��́A�ȉ~�̍��E�̒[�Ő~���ȉ~�ɐڂ���Ƃ��܂��B
�ڂ��Ă��Ȃ��Ƃ���ƁA�~�͒��a�����������ł�����邱�Ƃ��ł��܂��B
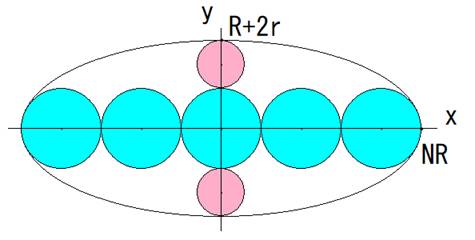
���ȉ~�̕������ׂ܂��B
�~��N�Ƃ���ƁAy���̉E�ɂ́A(N�|1)�^2�{0.5������܂��B
�~�̒��a��2R�Ƃ���ƁAx�ؕЂ́ANR�ƂȂ�܂��B
y�ؕЂ́AR�{2r�ł��B
����đȉ~�̕������́A
![]()
��ԉE�̐~�̕����������߂܂��B
![]()
(1)�A(2)��A�������܂��B
![]() ���A
���A
![]()
����2�����������Ax��NR���d���ɂ��Ă悢�̂ŁA���ʎ���0�Ƃ��ĉ����܂��B
![]()
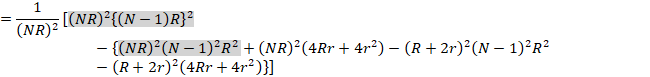
![]()
![]()
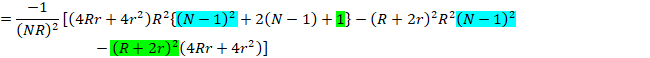
![]()
![]()
![]()
![]()
��
![]()
����̂悤�ɂł��܂����A�v�Z���ʓ|�ł��B
������(3)�́A���̂悤�Ɉ��������ł��܂��B
![]()
�E�̒��J�b�R�̂Ƃ��납���x��NR�̉��ƂȂ�͂��ł��B
����������āAN�ɂ��ĉ����ƁA
![]()
![]()
![]()
![]()
��
![]()
���2
�}��AOC���꒼���ɂȂ��Ă��܂����A���̕K�v�͂���܂���B
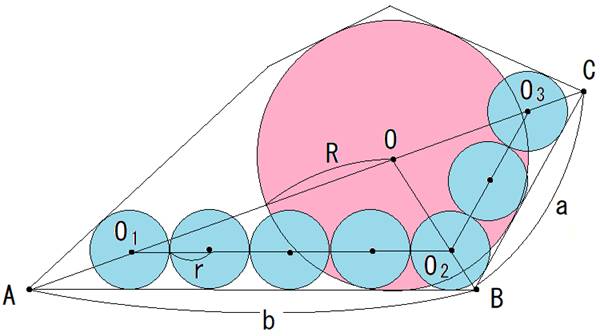
���ԉ~�̔��a��R�A�~�̔��a��r�Ƃ��܂��B
�}�Ł�OBC�䁢OO2O3�ł��B
��ӂƍ����̔�ׂ�ƁA![]()
![]()
��AB�ɂ����Đ~��N���ԂƂ��܂��B
����ƁAO1O2��2(N�|1)r�ł��B
��OAB�䁢O O1O2�ł��B
��ӂƍ����̔�ׂ�ƁA![]()
![]()
����̌��ʂƔ�r���āA
![]()
���3
���̖��̓����́u�E�E�E�̐��������v�Ƃ����̂��ƂĂ��q���g�ɂȂ�܂��B
��AB�����F�̉~�ɐڂ���Ƃ��čl���܂��B
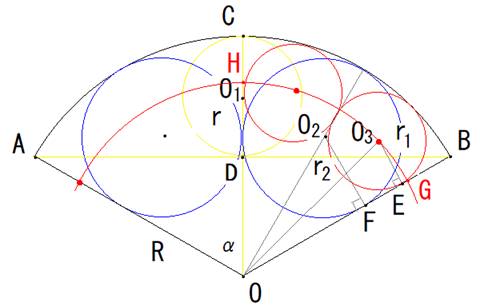
����AOD�����Ƃ��܂��B
�~O1�̔��ar�́A�~O2�̔��ar2�ŕ\���ƁA![]()
��OAD���A![]()
��OO2F���A![]()
����A![]()
����āA
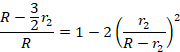
�������āA![]() �ƂȂ�܂����AR>r2 ���A
�ƂȂ�܂����AR>r2 ���A![]()
�܂�A��`�̔��a�́A���F�~�̒��a��2�{�Ȃ̂ŁACD��DO�ł��B
����āA![]() �ł��B
�ł��B
���Ԃ̉~��z�u���A���a(R�|r1)�ŁA���SO�̐�`��`���܂��B
����HG�̒��Ɍ�O3G���������邩�𐔂���悢�킯�ł��B
�������A��O3G�̒�����������Əo���̂́A����̂ŁA��O3G�aO1�̒����ŁA��p���܂��B
��HG�̒����́A���a�~���S�p��苁�܂�̂ŁA
![]()
�����̌��ʂ́A�ԉ~�Ɛ~�������傫���̂Ƃ��ir2��r1�j�A���������ʂƂȂ�܂��B
�ʂ̒����𐂐��̒����ő�p����̂ŁA���S�p���������قnj덷���������Ȃ�܂��B
�{���̒l��菬���Ȓl�Ŋ���̂ŗ]�肪�o�܂����A������̂Ă�Ηǂ��킯�ł��B
�Ⴆ�A�ԉ~�Ɛ~�̑傫���������Ƃ����(����60��)�A
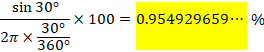
![]()
���̂Ƃ��́A22���傫���l������ƁA�����Ⴂ�܂��B
�������A�ԉ~���������Ȃ�ɘA��ǂ�ǂ�덷���������Ȃ�̂Ō����I�ɂ͖�肠��܂���B
���4
�}�̂悤�ɁA�e�_��\���܂��B
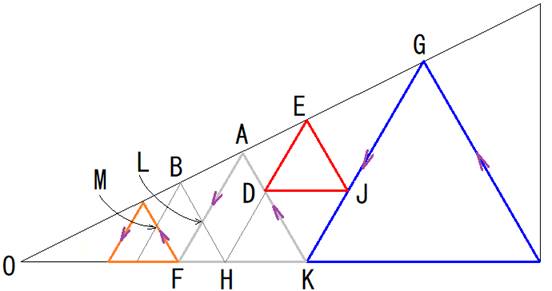
�����p�O�p�`�̒��ɁA�A���A���F�̐��O�p�`�͊ȒP�ɔz�u�ł��܂��B
�����ɁA�Ԃ̐��O�p�`��z�u���܂��B
�����Ȑ��O�p�`�̒�K��p�ӂ��A���p�O�p�`�̎Ε�OG��ɒ��_��u���Ȃ���
���łɔz�u����Ă���A���O�p�`�ƕӂs�ɕۂ��Ȃ��瓮�����܂��B
��K��AK�AGK�Ƃ̌�_�����Ԑ�����ӂɕ��s�ƂȂ�Ƃ��̒��_��E�Ƃ��܂��B
���̂Ƃ��A��K��AK�Ƃ̌�_��D�Ƃ��܂��B
����ŐԂ̐��O�p�`�����܂�܂��B
�������āAED�ƒ�ӂƂ̌�_��H�Ƃ��܂��B
H����AK�ƕ��s�ɐ��������AOG�Ƃ̌�_��B�Ƃ��܂��B
���l�p�`EDKJ�͕��s�l�ӌ`�ł��B
��́�EDJ�Ɖ��́�KJD�͂Ƃ��ɐ��O�p�`�ł��B
DJ�����ʂȂ̂ŁAED��DK�ƂȂ�܂��B
��DHK�����O�p�`�ł��B
����āADH��DK��ED�ł��B
��EAD�䁢EBH�ł��B
ED=DH�Ȃ̂ŁAAD�FBH��1�F2�ł��B
��BLA�䁢BHE�ł��B
LA�FHE��1�F2�Ȃ̂ŁABL�FLH��1�F1�ł��B
��LFH�͐��O�p�`�ł��B
����܂���ƁA�l�p�`BMFL�͕��s�l�ӌ`�ł����A�ׂ荇��2�ӂ��������̂ŕH�`�ł��B
����ƁA��BML�͐��O�p�`�ɂȂ�܂��B
������ƁADJ=HK�AML=FH�ł��B
x��FK��FH�{HK��ML�{DJ��b�{a�ƂȂ�܂��B
���N���̂�������@�@�lj����̉ł��B
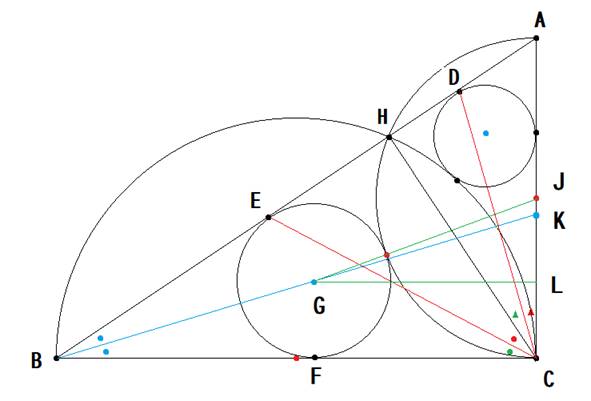
��2�̔��~�̌�_��H�A���̉~�̒��S��G�A�E�̔��~�̒��S��J�ABG�̉�����AC�̌�_��K�A
G����BC�ւ̐����̑���F�AAC�ւ̐����̑���L�Ƃ��܂��B
H��C�����ԂƁA���a�ɂ��~���p��90�x�Ȃ̂ŁAH�͒��p�O�p�`�̎Εӏ�ɂ���܂��B
�����ł́A��BCH��CE�łQ��������邱�Ƃ������܂��B
��ACH��CD��2��������邱�Ƃ����l�ɂ�����̂ŁA���킹�Ē��p�ɂȂ�Q�̊p�̔������Ȃ̂Ł�DCE��45���Ƃ������Ƃł��B
�}�̒��������̂悤�ɂ��܂��B
AB��c�ABC��a�ACA��b�ABF��p
������� ![]() �ł��B
�ł��B
����ABC�́ABK�œ������̂ŁACK�FCA��a�Fc �ł��B
����āA
![]()
����ABC�䁢ACH�䁢CBH�Ȃ̂ŁA
AB�FBC�FCA��c�Fa�Fb
AC�FCH�FHA��b�FCH�FHA
CB�FBH�FHC��a�FBH�FHC
����āA
![]()
����BFG�䁢BCK�Ȃ̂ŁABF�FBC��FG�FCK
����āA
![]()
����JGL�͒��p�O�p�`�ł��B
JG�́A���̉~�̔��a�ƉE�̔��~�̔��a�̘a�ł��B
GL�́ABC�|BF�ł��B
LJ��JC�|GF�ł��B
����āA
![]()
![]()
p�ɂ��ĉ����ƁAp��c��菬�����̂ŁA
![]()
�����ɁABE�AHE�ACE�����߂܂��B
BE��BF�Ȃ̂ŁABE��BF��p��c�|b
HE��BH�|BE�Ȃ̂ŁA
![]()
��CEH�́A���p�O�p�`�Ȃ̂ŁA
![]()
�������ŁA��HCE����ECB�������܂��B
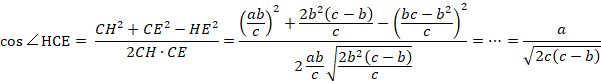
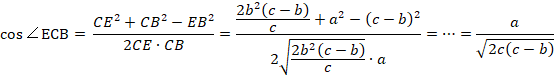
����āA��HCE����ECB�ł��B
�����l�ɁA��ACH��CD��2��������邱�Ƃ�������̂ŁA��DCE��45�x�ł��B
�����̗���F�o�T����Q�l�ɂ����ł����@04/12 14��00�� �X�V 4/12

NO3�u�O�p��K�v�@�@�@�@ 04/12 14��06���@��M �X�V 4/12
�W���[�J�[����̒lj������������܂����B
�����̗���F�Y��ȉ�@�ł���
NO1�u�W���[�J�[�v�@�@ 04/12 20��06���@��M �X�V 4/13
�o��҂�������ł��B
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
