�����Q�O�N�U���P�T��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��Q�O�W�����w�I�ȉ������
�@�@�@�@�@�@����W���ԁF�T���P�W���`�U���P�T��
�m���a�n
�F����A�ݏ�a�i���j�̌��������@�������m�ł����B
�ߋ��̑�w�����������Ă�����A�k���H�Ƒ�w��2002�N�ɉ��̂悤�Ȗ�肪�łĂ��܂����B
�ꕔ���肵�Ă��܂��B���k�ɂ͋���������@�ł��B

�F����A�������킩������A�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA
���[���ő����Ă��������B�҂��Ă��܂��B
NO1�uuchinyan�v 5/18 12��22����M
�X�V6/15
��Q�O�W�w�I�ȉ�����
�m���a�n
�Ƃɂ����C�w���ɏ]���Čv�Z���Ă����܂��B
(1)
a(n) = {n(n-1)}^2
b(n) = a(n+1) - a(n)
= {(n+1)n}^2 - {n(n-1)}^2
= n^2 * {(n+1)^2 - (n-1)^2}
= n^2 * {(n^2 + 2n + 1) - (n^2 - 2n + 1)}
= n^2 * {4n}
= 4n^3
(2)
��[k=1,n]b(k) = a(n+1) - a(1)
��[k=1,n]{4k^3} = {(n+1)n}^2 - 0
��[k=1,n]{k^3} = 1/4 * {n(n+1)}^2
(3)
a(n) = {n(n-1)}^3
b(n) = a(n+1) - a(n)
= {(n+1)n}^3 - {n(n-1)}^3
= n^3 * {(n+1)^3 - (n-1)^3}
= n^3 * {(n^3 + 3n^2 + 3n + 1) - (n^3 - 3n^2 + 3n - 1)}
= n^3 * {6n^2 + 2}
= 6n^5 + 2n^3
(4)
��[k=1,n]b(k) = a(n+1) - a(1)
��[k=1,n]{6k^5 + 2k^3} = {(n+1)n}^3 - 0
��[k=1,n]{k^5} = 1/6 * [{n(n+1)}^3 - 2 * ��[k=1,n]{k^3}]
= 1/6 * [{n(n+1)}^3 - 2 * 1/4 * {n(n+1)}^2]
= 1/12 * n^2 * (n+1)^2 * (2n^2 + 2n - 1)
(5)
a(n) = {n(n-1)}^4
b(n) = a(n+1) - a(n)
= {(n+1)n}^4 - {n(n-1)}^4
= n^4 * {(n+1)^4 - (n-1)^4}
= n^4 * {(n^4 + 4n^3 + 6n^2 + 4n + 1) - (n^4 - 4n^3 + 6n^2 - 4n + 1)}
= n^4 * {8n^3 + 8n}
= 8n^7 + 8n^5
(6)
��[k=1,n]b(k) = a(n+1) - a(1)
��[k=1,n]{8k^7 + 8k^5} = {(n+1)n}^4 - 0
��[k=1,n]{k^7} = 1/8 * [{n(n+1)}^4 - 8 * ��[k=1,n]{k^5}]
= 1/8 * [{n(n+1)}^4 - 8 * 1/12 * n^2 * (n+1)^2 * (2n^2 + 2n - 1)]
= 1/24 * n^2 * (n+1)^2 * {(3n^4 + 6n^3 + 3n^2) - (4n^2 + 4n - 2)}
= 1/24 * n^2 * (n+1)^2 * (3n^4 + 6n^3 - n^2 - 4n + 2)
(7)
a(n) = {n(n-1)}^5
b(n) = a(n+1) - a(n)
= {(n+1)n}^5 - {n(n-1)}^5
= n^5 * {(n+1)^5 - (n-1)^5}
= n^5 * {(n^5 + 5n^4 + 10n^3 + 10n^2 + 5n + 1) - (n^5 - 5n^4 + 10n^3 - 10n^2 +
5n - 1)}
= n^5 * {10n^4 + 20n^2 + 2}
= 10n^9 + 20n^7 + 2n^5
(8)
��[k=1,n]b(k) = a(n+1) - a(1)
��[k=1,n]{10k^9 + 20k^7 + 2k^5} = {(n+1)n}^5 - 0
��[k=1,n]{k^9} = 1/10 * [{n(n+1)}^5 - 20 * ��[k=1,n]{k^7} - 2 * ��[k=1,n]{k^5}]
= 1/10 * [{n(n+1)}^5 - 20 * 1/24 * n^2 * (n+1)^2 * (3n^4 + 6n^3 - n^2 - 4n + 2)
- 2 * 1/12 * n^2 * (n+1)^2 * (2n^2 + 2n - 1)]
= 1/60 * n^2 * (n+1)^2 * {6n^3 * (n^3 + 3n^2 + 3n + 1) - 5 * (3n^4 + 6n^3 - n^2
- 4n + 2) - (2n^2 + 2n - 1)}
= 1/60 * n^2 * (n+1)^2 * (6n^6 + 18n^5 + 3n^4 - 24n^3 + 3n^2 + 18n - 9)
= 1/20 * n^2 * (n+1)^2 * (2n^6 + 6n^5 + n^4 - 8n^3 + n^2 + 6n - 3)
= 1/20 * n^2 * (n+1)^2 * (n^2 + n - 1)(2n^4 + 4n^3 - n^2 - 3n + 3)
�Ō�̈��������́CWeb�Œ��ׂē������킹�����ĉ\�Ȃ��Ƃ�m��܂��� (^^;
(���z)
�ȗ����܂����C��ʂ� a(n) = {n(n-1)}^m ���g���C�����C���a�����߂���悤�ł��B
�Ȃ��Ȃ����܂����@���Ǝv���܂����B
�Ȃ��C��ʂ̏ꍇ�́C��P�U�Q��Ō������܂����B
NO2�ukashiwagi�v 5/20 20��13����M �X�V6/15
�K�����炱�̂悤�ȑf���炵�����̓W�J���o����Ƃ́E�E�E�E�A���ɖڂ���ł��B ���̕����͐�ɋL�����Ă������l������܂��ˁB
208���
�i1�j![]()
�i2�j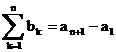 �@�ł��邩��A�i1�j�𗘗p���āA
�@�ł��邩��A�i1�j�𗘗p���āA
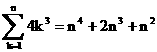 �@�@�����āA�@
�@�@�����āA�@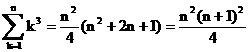
![]()
�i3�j�ȍ~���S�āi1�j�A�i2�j�Ɠ��l�̌v�Z������Ηǂ��̂ŁA�r���̉ߒ������ĉ̂f����B
�i3�j![]()
�i4�j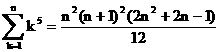
�i5�j![]()
�i6�j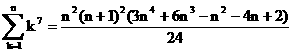
�i7�j![]()
�i8�j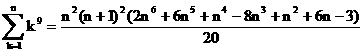
NO3�ubear56�v 5/20 20��14����M �X�V6/15
���Ɏ菇��������Ă���̂ŁC���C��������Ă���悤�Ȗ��ł����D(^_^;)
��ꂽ���ł��BNO4�ukasama�v 6/12 15��57����M �X�V6/15
����ɂ��́A�����A���쐬�����l�ł��B
�K�������܂����p����ƁA��������̘a�����X�ɋ��߂邱�Ƃ��ł���̂ł��ˁB���ɂȂ�܂����B
|
(1) |
bn=an+1-an={(n+1)n}2-{n(n-1)}2=4n3 |
|
(2) |
|
|
|
|
|
(3) |
bn=an+1-an={(n+1)n}3-{n(n-1)}3=2n3+6n5 |
|
(4) |
���l�ɂ��āA |
|
|
|
|
(5) |
bn=an+1-an={(n+1)n}4-{n(n-1)}4=8n5+8n7 |
|
(6) |
���l�ɂ��āA |
|
|
|
|
(7) |
bn=an+1-an={(n+1)n}5-{n(n-1)}5=2n5+20n7+10n9 |
|
(8) |
���l�ɂ��āA |
|
|
|
|
|
|
![]()
