平成２２年３月２８日

[流れ星]

　　　　　第238回数学的な応募問題解答

　　　　　　＜解答募集期間：3月7日〜3月28日

［有名ないい話］

2005年に東北大学の入試問題は結果がいい話になる有名な問題でした。

ここに紹介します。

NO1「uchinyan」 03/07 17時15分受信

「uchinyan」 03/08 11時08分受信 更新3/28

(1)

k 回目に取り出したカードの数字を a(k) とします。

得点が k になるのは，k-1 回目までは終了せずに，k 回目で終了する場合です。

これは，

a(1) < a(2) < ... < a(k-1), a(k) <= a(k-1)

です。そこで，a(k-1) = m として，

k 回目の a(k) は 1 〜 m の m 通り

k-1 回目の a(k-1) = m は k-1, k, ..., n のいずれか

k-2 回目までは 1 〜 m-1 から k-2 枚を選び小さい順に並べればよく (m-1)C(k-2) 通り

なので，求める確率 p(k) は，

p(k) = Σ[m=k-1,n]{(m-1)C(k-2)/n^(k-2) * 1/n * m/n}

= 1/n^k * Σ[m=k-1,n]{m * (m-1)C(k-2)}

= 1/n^k * Σ[m=k-1,n]{m * (m-1)!/(m-k+1)!(k-2)!}

= 1/n^k * Σ[m=k-1,n]{(k-1) * m!/(m-k+1)!(k-1)!}

= (k-1)/n^k * Σ[m=k-1,n]{mC(m-(k-1))}

= (k-1)/n^k * Σ[i=0,n-k+1]{(i+k-1)Ci}

= (k-1)/n^k * ((k-1)C0 + kC1 + (k+1)C2 + (k+2)C3 + ... + (n-1)C(n-k) + nC(n-k+1))

= (k-1)/n^k * (kC0 + kC1 + (k+1)C2 + (k+2)C3 + ... + (n-1)C(n-k) + nC(n-k+1))

ここで，二項係数の性質

(p-1)C(q-1) + (p-1)Cq = (p-1)!/(p-q)!(q-1)! + (p-1)!/(p-q-1)!q! = p!/(p-q)!q! = pCq

を繰り返し用いて，

= (k-1)/n^k * ((k+1)C1 + (k+1)C2 + (k+2)C3 + ... + (n-1)C(n-k) + nC(n-k+1))

= (k-1)/n^k * ((k+2)C2 + (k+2)C3 + ... + (n-1)C(n-k) + nC(n-k+1))

= (k-1)/n^k * ((k+3)C3 + ... + (n-1)C(n-k) + nC(n-k+1))

= ...

= (k-1)/n^k * ((n-1)C(n-k-1) + (n-1)C(n-k) + nC(n-k+1))

= (k-1)/n^k * (nC(n-k) + nC(n-k+1))

= (k-1)/n^k * (n+1)C(n-k+1)

p(k) = ((k-1) * (n+1)Ck)/n^k

になります。

(別解)

次のように考えれば，もっと簡単にできますね。

k 回目に取り出したカードの数字を a(k) とします。

得点が k になるのは，k-1 回目までは終了せずに，k 回目で終了する場合です。

これは，

a(1) < a(2) < ... < a(k-1), a(k) <= a(k-1)

ですが，

a(1) < a(2) < ... < a(k-1), a(k) は 1 〜 n のいずれか

の場合から

a(1) < a(2) < ... < a(k-1) < a(k)

の場合を引いたもの，と同じです。

そこで，まず，

a(1) < a(2) < ... < a(k-1), a(k) は 1 〜 n のいずれか

k 回目の a(k) は 1 〜 n の n 通り

k-1 回目までは 1 〜 n から k-1 枚を選び小さい順に並べればよく nC(k-1) 通り

なので，n * nC(k-1) 通り。

次に，

a(1) < a(2) < ... < a(k-1) < a(k)

1 〜 n から k 枚を選び小さい順に並べればよく nCk 通り。

前者から後者を引くと，

n * nC(k-1) - nCk

= n * n!/(n-k+1)!(k-1)! - n!/(n-k)!k!

= n!/(n-k+1)!k! * (nk - (n-k+1))

= n!/(n-k+1)!k! * (n+1)(k-1)

= (k-1) * (n+1)!/(n+1-k)!k!

= (k-1) * (n+1)Ck 通り

そこで，求める確率 p(k) は，

p(k) = ((k-1) * (n+1)Ck)/n^k

になります。

(2)

f(n) = Σ[k=2,n+1]{k * p(k)}

= Σ[k=2,n+1]{k * ((k-1) * (n+1)Ck)/n^k}

= Σ[k=1,n]{k(k+1) * (n+1)C(k+1) * 1/n^(k+1)}

= Σ[k=1,n]{k(k+1) * (n+1)!/(k+1)!(n-k)! * 1/n^(k+1)}

= (n+1)/n * Σ[k=1,n]{(n-1)!/(k-1)!(n-k)! * 1/n^(k-1)}

= (n+1)/n * Σ[k=0,n-1]{(n-1)!/k!(n-k-1)! * 1/n^k}

= (n+1)/n * Σ[k=0,n-1]{(n-1)Ck * 1/n^k}

ここで，二項定理より，

(1 + x)^(n-1) = Σ[k=0,n-1]{(n-1)Ck * x^k}

なので，x = 1/n として，

(1 + 1/n)^(n-1) = Σ[k=0,n-1]{(n-1)Ck * 1/n^k}

そこで，

f(n) = (n+1)/n * (1 + 1/n)^(n-1) = (1 + 1/n)^n

これより，

lim[n->∞]{f(n)} = lim[n->∞]{(1 + 1/n)^n} = e = 2.71828...

になります。

(感想)

「有名」とは知りませんでしたが，確かに，「いい」話でした (^^;

最初，題意を勘違いしていて「いい」話にならず，首を傾げていましたが，

間違いに気付き何とかできました。

しかし，(1)が少し複雑だったのですが，(別解)のようにもっと簡単にできました。

試験場では，(別解)のようにやらないと厳しそうですね。

NO2「ｽﾓｰｸﾏﾝ」 　03/11 21時46分受信

NO3「kashiwagi」 03/22 08時29分受信 更新3/28

＜コメント：お世話になります。今回の問題は組み合わせの公式である
ｎCr=n-1Cr-1+n-1Crに中々気づかず、どうしたら解けるのかと懊悩煩悶を繰り返しておりました。ところが、昨夜何気なく大学時代の教科書を翻とくと・・・・・、やっと解答を送付することが出来
そうです・・・・。しかし、値は・・・・、信じられない・・・・。＞

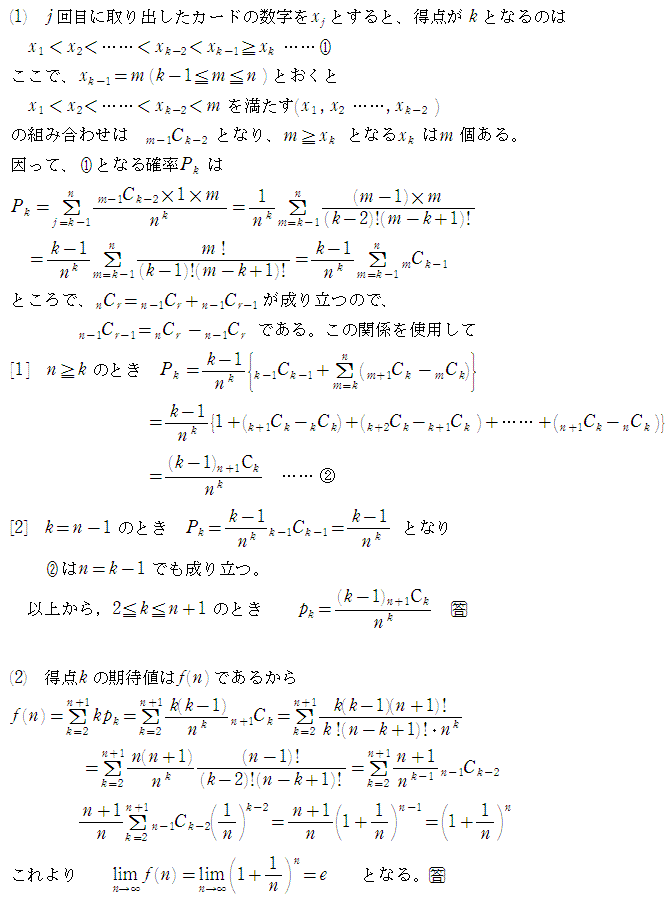
NO4「再出発」 　 03/24 00時23分受信 更新3/28

＜コメント：こんな問題を制限時間内に完答する受験生がいるんでしょうか？
私はいろいろ試行錯誤もありまして、随分時間が掛かりました。＞

寄せられた解答です。

＜コメント：階段を上る問題や、モンモールの問題のように漸化式もどきを考えたのですが、難問でした。最後に「いいはなし」の謎が解けたときは感動的でした。
出題された方に敬意を表したいと思います。＞

皆さん、答えがわかったら、一部でも構いませんから、解答とペンネームを添えて、
メールで送ってください。待っています。