平成15年7月27日
第3回 「フィボナッチ数列を発見しよう」
6月23日、6月30日、7月7日実施
来週から、「フィボナッチ数列」またはフィボナッチについて学習するから、調べてきなさい。
1. 生徒の調べ学習から
2.
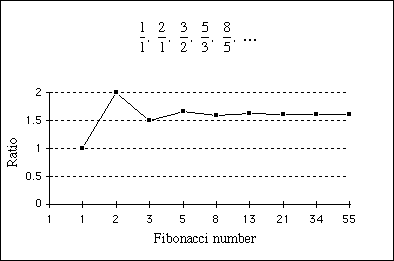
(1)フィボナッチFibonacciの数列は 1,1,2,3,5,8,13,21,34,55,・・・
という数列をいう。
(2)数列{Fn}において、F1=1,F2=1,Fn+2=Fn+Fn+1 をいう。
(3)ヒマワリや松の種子の配列など、自然界にしばしば見られる。

(http://plus.maths.org/issue3/fibonacci/ から引用)
(4)隣接する2項の比 Fn+1/Fn が黄金比(1+√5)/2=1.618に近づく
一連の数列をいう。また、黄金比を連分数で表すことができる。
(http://plus.maths.org/issue3/fibonacci/ から引用)
(5)フィボナッチ(1170頃〜1250)は13世紀に活躍したイタリアの数学者で、1202年に、15章からなる大書「算盤の書」を書いた。
3. 課題提供:「フィボナッチ数列」について関連するものがあるから、考えてみよう。
4.
『1』「算盤の書」の第12章に、ウサギのつがいの問題として有名な問題がある。
問題:「ある人が壁で囲まれた場所に1つがいの親ウサギを入れました。1年間に何つがいのウサギが増えるでしょうか。ただし、どのつがいも生まれて2ヶ月目から毎月1つがいのウサギを産むものとする。
また、ウサギは一切、死なないこととする。このとき、この月数とウサギのつがい数を調べよう。
『2』自然界でまだ、フィボナッチ数列と深い関係があるものもあるから、調べよう。
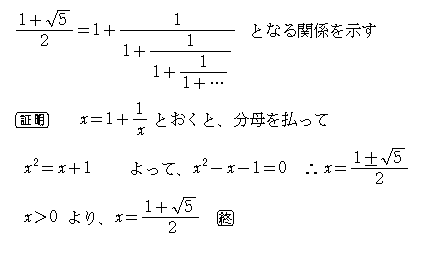
『3』黄金比を数字の「1」だけで、連分数として表すことができるから、考えよう。
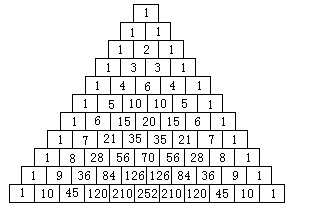
『4』パスカルの三角形の中に、フィボナッチ数列が隠されているから発見しょう。
『5』今、旬なものは 大相撲名古屋場所ですね。ここで、問題です。
「偉大な横綱は連敗しないのが、優勝の条件のようです。そこで、15日間2連敗しない、勝ち負けの勝敗の起こり方は何通りでしょう?また、一般の場合はどうなるでしょう?」
例えば、 1日目 「○」か「×」の2通り。
2日目 「○○」「○×」「×○」の3通り。
3日目 「○○○」「○○×」「○×○」「×○○」「×○×」の5通り。
4日目 「○○○○」「○○○×」「○○×○」「○×○○」
「×○○○」「×○×○」「×○○×」「○×○×」の8通り。
『6』問題:「2×nの長方形に2×1の長方形を敷き詰める方法の数を調べよう。」
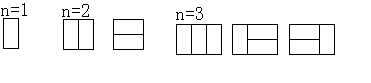
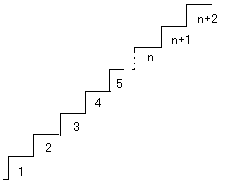
『7』問題:「階段を上がるのに、1度に1段、または2段上がってよいことにする。このとき、n段の階段を上がる方法の数を調べよう。」
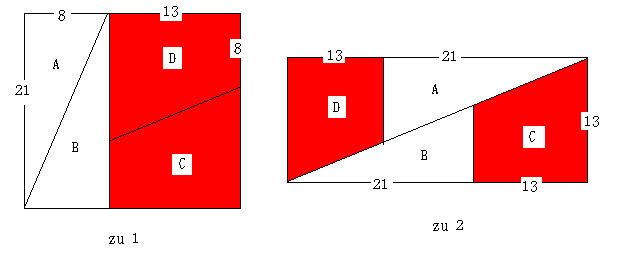
『8』問題:「最初 1辺が21cmの正方形を下の図のように4つの部分に分けました。
三角形Aと三角形Bは合同、三角形Cと三角形Dは合同です。次に、この4つを移動させて、[zu2]の図形を作りました。見た目は長方形ですから、面積を考えてみると、横13cm、縦(13+21)cmになります。4つの部分を移動しただけですから、面積は同じになるはずです。
どうして、1cm2違うのでしょうか。この違いは、「フィボナッチ数列」にどんな性質があるからでしょうか。」
『9』次の性質が成り立つことを調べよう。(生徒にはまだ、知らせていない)
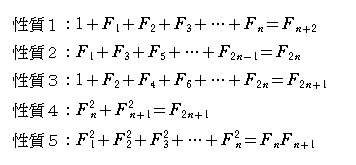
『10』フィボナッチ数列の母関数を調べよう。(生徒にはまだ、知らせていない)

3.生徒の感想
『1』・頑張って解いた結果、ちゃんと証明も出来て良かった。図に表していくと結構分かりやすい。
『4』・パスカルの三角形を斜めに加えると、フィボナッチになるとは驚いた。
・パスカルの三角形の中に、フィボナッチを発見したときはとても達成感が味わえた。これからも
楽しい数学で解けた喜びを味わえるように頑張りたい。
・フィボナッチ数列を見つけたけれど、どうしてそうなるか証明は、できていない。このままでは楽し
い数学にならないので、もっと考えて分かる喜びを感じたい。
・フィボナッチの学習は始め、公式や記号で難しい所があったが、結構身近な例があり、驚きました。
『5』・世の中にもフィボナッチ数列が見られたので、これからも研究していきたい。
・多くの問題を考えて、最終的な答えがフィボナッチ数列になっていることが分かり、自分でもフィボナッチ数列が関係している問題を研究したい。
・フィボナッチ数列の2項の比が黄金比でできていたり、不思議な法則があったりして、驚いた。
・フィボナッチ数列がいろんなところで使われていることが分かった。何となくフィボナッチ数列が分かったような気がする。
『6』・2種類の長方形を順に組み合わせていくと、フィボナッチ数列なるとは思わなかったが、成り立っていると分かったとき、うれしかった。
『7』・階段登りにフィボナッチ数列が関係していたし、成り立つことが分かった。
・フィボナッチ数列を学習してみて、今まで名前も知らなかったけど、数列に規則があることなどいろいろと知ることができた。
・身の回りに、フィボナッチ数列がいろんなところであることが分かった。今度、階段を登るとき確かめたい。
・すべての場合を数えていくと大変だけど、(n+2)番目を(n+1)番目とn番目の階段を考える と、フィボナッチの規則になり、楽だった。機会があったらもっと詳しく調べたい。
『8』・図2で、対角線の傾きが違うから、直線でないことに気がついた。面積がなぜ1cm2違うのかは分かりません。
・ 図2で実際に、面積を調べたら441cm2だから、442cm2 になるのは間違い。
4.シュタイナー教育とフィボナッチ数列(数のイメージを2つのグループで暗唱する)
|
Aグループ Bグループ |
|
Aグループ Bグループ |
|
一 … 一 二 … 三 フィボ … ナッチ 数列 … 数列 五 … 八 十三 … 二十一 まだ続く … まだ続く お尻の二つの… 足し算したのが 次の数 … 次の数 らせん … 一 笠松 … 一 六角形 … 二 |
パイナップル … 三 巻き貝 … 五 木の葉 … 八 花 … 十三 果物 … 二十一 葉のつき方 … 三十四 黄金比 … 五十五 いろんな場所に… 現れる 自然の中に … パスカルの三角形に 星型五角に … 無限の数列 黄金 … 分割 フィボ … ナッチ 数列 … 数列 |
<参考文献>
1.フィボナッチ数の小宇宙 中村 滋 著 日本評論社
2.シュタイナー学校の数学読本 ベングト・ウリーン著 丹羽敏夫・森章吾 共訳 三省堂
3.私のまわりは美しい 松井 るり子 著 学陽書房
4.理系への数学 2000年11月号 現代数学社
5.「数の悪魔」 エンツェンスベルガー 著 丘沢 静也 訳 晶文社
6.折る紙の数学 渡部 勝 著 講談社
<参考および関連したウェブサイト>
1.The life and numbers of
Fibonacci
http://plus.maths.org/issue3/fibonacci/
2.水の流れ(小生のホームページ) http://www2.ocn.ne.jp/~mizuryu/
