�����Q�V�N�P�P���Q�Q��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��327�����w�I�ȉ����
�@�@�@�@�@�@����W���ԁF10��25���`11��22����
�m���͐��O�p�`�n
�@�F����B�����͕������Ă��邪����������ςȖ�肪����܂��B���̒��ō���̖�肪����܂��B
���a���̉~�ɓ��ڂ���O�p�`�̖ʐς̍ő�l�����߂�B
�Q�l�F�ǂ��ɕϐ������A���ꂪ1�ϐ���2�ϐ����ʼn�@�̖������܂�Ă��܂��B
NO1�uuchinyan�v
10/25 16��51���@��M
�uuchinyan�v 10/28
11��28���@��M �X�V 11/22
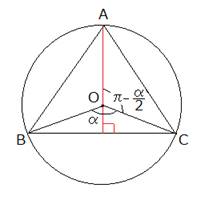
�ȉ��ł́C���a r �̉~�̒��S�� O�C�O�p�`�� ��ABC�C�Ƃ��܂��B
(��@1)
O �� ��ABC �́C�O���C�ӏ�C�����̂����ꂩ�ɂ���܂��B
O �� ��ABC �̊O���ɂ���ꍇ
��ABC �͓݊p�O�p�`�ŁC��BAC > 90���C�Ƃ��ď\���ł��B
���̂Ƃ��CA ���� BC �ɐ��������낵���̑��� H�CBC �̒��_�� M�CM ���� BC �ɒ���������������C
�~�Ƃ̌�_���CBC �Ɋւ� A �̂������ D�C���Α��� E�C�Ƃ���C
AH <= DM < EM�CDE��BC�C��ABC = BC * AH * 1/2 <= BC * DM * 1/2 < BC * EM * 1/2 = ��EBC�C�ŁC
O �� EM ��ɂ���̂� ��EBC �̓����ɂ���CO ���O�p�`�̓����ɂ��� ��EBC ���l����Ώ\���ł��B
O �� ��ABC �̕ӏ�ɂ���ꍇ
��ABC �͒��p�O�p�`�ŁCO �� BC ��C��BAC = 90���C�Ƃ��ď\���ł��B
���̂Ƃ��CAB �̒��_�� M�CM ���� AB �ɒ���������������C
AB �Ɋւ� C �̂�����̉~�Ƃ̌�_�� E �Ƃ���C
CA < EM�C��ABC = AB * CA * 1/2 < AB * EM * 1/2 = ��EAB�C�ŁC
O �� EM ��ɂ���̂� ��EAB �̓����ɂ���CO ���O�p�`�̓����ɂ��� ��EAB ���l����Ώ\���ł��B
O �� ��ABC �̓����ɂ���ꍇ
��ABC �͉s�p�O�p�`�ŁC��AOB = ���C��BOC = ���C��COA = ���C�Ƃ���ƁC
���C���C���͂Ƃ��� 0�����傫�� 180����菬�����C�� + �� + �� = 360���C�ł��B�����āC
��ABC = ��OAB + ��OBC + ��OCA = r^2/2 * (sin�� + sin�� + sin��)�C
�����ŁC���C���C���͂Ƃ��� 0�����傫�� 180����菬�����C�̂ŁC
y = sin(x) �̃O���t�� 0���` 180���͈̔͂ōl����ƁC��ɓʂȂ̂ŁC
(sin�� + sin��)/2 <= sin((�� + ��)/2)�C
�����́C�� = ���C�ł��B����ɁC0��< (�� + ��)/2 <
180���C�Ȃ̂ŁC
(2 * sin((�� + ��)/2) + sin��)/3
<= sin((2 * (�� + ��)/2 + ��)/3) = sin((�� + �� + ��)/3)�C
�����́C(�� + ��)/2 = ���C�ł��B���̓���C
(sin�� + sin�� + sin��)/3 =
(2 * (sin�� + sin��)/2 + sin��)/3
<= (2 * sin((�� + ��)/2) + sin��)/3 <= sin((�� + ��
+ ��)/3)�C�����́C�� = �� ���� (�� + ��)/2 = ���C
(sin�� + sin�� + sin��)/3
<= sin((�� + �� + ��)/3)�C�����́C�� = �� = ���C
���̕s�������̂� y = sin(x) �̃O���t�̐�������C���C���C�����Ƃ��� 0���` 180���͈̔͂Ȃ��ʓI�ɐ������܂��B
���͓��ɁC�� + �� + �� = 360���C�Ȃ̂ŁC
(sin�� + sin�� + sin��)/3
<= sin((�� + �� + ��)/3) = sin(360��/3) = sin(120��) = ��3/2�C
�����́C�� = �� = �� = 120���C����� ��ABC �����O�p�`�C�ł��B�����ŁC
��ABC = r^2/2 * (sin�� + sin�� + sin��) <= r^2/2 * (��3/2 * 3) = (3��3/4)r^2�C
�ƂȂ��āC�ʐς̍ő�́C��ABC �͐��O�p�`�C�̂Ƃ��ŁC(3��3/4)r^2�C�ɂȂ�܂��B
(��@2)
�~O �� ��ABC �̊O�ډ~�ɂȂ��Ă���̂ŁC
�����藝���CBC = (2r)sinA�CCA =
(2r)sinB�CAB = (2r)sinC�C�ŁC
��ABC = AB * AC * sinA * 1/2 = (2r^2)sinAsinBsinC�C
�����ŁCsinA�CsinB�CsinC �͐��̐��Ȃ̂ŁC�������敽�ς��C
(sinAsinBsinC)^(1/3) <= (sinA + sinB +
sinC)/3�C������ A = B = C�C
����ɁCA�CB�CC �͂Ƃ��� 0�����傫�� 180����菬�����CA + B + C = 180���C�Ȃ̂ŁC
(��@1)�Ɠ��l�� y = sin(x) �̃O���t�� 0���` 180���͈̔͂ōl���āC
(sinA + sinB + sinC)/3 <= sin((A + B +
C)/3) = sin(180��/3) = sin(60��) = ��3/2�C
�����́CA = B = C = 60���C�ł��B�����ŁC
(sinAsinBsinC)^(1/3) <= (sinA + sinB +
sinC)/3 <= ��3/2�C
�������C�����͂ǂ���̕s�������CA = B = C�C�̂Ƃ��C�ł��B������C
��ABC = (2r^2)sinAsinBsinC <= (2r^2)(��3/2)^3 <= (3��3/4)r^2�C��̕s�����̓����� A = B = C = 60���C
�ƂȂ��āC�ʐς̍ő�́C��ABC �͐��O�p�`�C�̂Ƃ��ŁC(3��3/4)r^2�C�ɂȂ�܂��B
(����)
(��@2)�́C�ꌩ����ƁC
(sinAsinBsinC)^(1/3) <= (sinA + sinB +
sinC)/3�C������ A = B = C�C
�̂Ƃ���ŁCA + B + C = 180���C�ƍ��킹�āCA
= B = C = 60���C���O�p�`���ő�C�Ƃ��Ă悳�����ł����C
���̎��_�ł́CsinA + sinB + sinC�C���m�肵�Ă��炸�CA = B = C �ȊO�ōő�����\��������̂ŁC
����͘_���I�ɐ������Ȃ��C����ȍ~�̋c�_�͕K�{�ł��B���ӂ��K�v�ł��B
(��@3)
A ���� BC �ɐ��������낵���̑��� H �Ƃ��܂��B
BC ���Œ肵 A �����ƁC��ABC = BC * AH * 1/2�C�Ȃ̂ŁCAH ���ő�̂Ƃ� ��ABC �͍ő�ł��B
AH ���ő�̂Ƃ��́C�~�̑Ώ̐����C��ABC �� AB = AC �̓ӎO�p�`�̂Ƃ��ł��B
�����ŁC���̏ꍇ�Ɍ��肵�čl���Ă悭�C��BOH = �ƁC0
< �� < �C�Ƃ����ƁC
BC = BH * 2 = (2r)sin�ƁCAH = AO + OH = r(1 + cos��)�C���C
��ABC = (2r)sin�� * r(1 + cos��) * 1/2 = r^2 * (sin�� + sin��cos��)�C
f(��) = sin�� + sin��cos��
�Ƃ����ƁC
f'(��) = cos�� + (cos��)^2
- (sin��)^2 = 2(cos��)^2 + cos�� - 1 = (2cos�� - 1)(cos�� + 1)�C
0 < �� < �Ccos�� + 1
>= 0�C���C
cos�� = 1/2�C�� = ��/3�C�ŋɑ傩�ő�ŁCf(��) �̍ő�l�� 3��3/4�C�ł��B
�����ŁC��ABC �̍ő�́C��BOC = ��BOH * 2 = 2��/3�C���O�p�`�̂Ƃ��ŁC(3��3/4)r^2�C�ɂȂ�܂��B
(��@4)
(��@3)�Ɠ��l�ɁC��ABC �ɂ����āC
BC ���Œ肵 A �����ƁC��ABC ���ő��
AB = AC �̓ӎO�p�`�̂Ƃ��C
CA ���Œ肵 B �����ƁC��ABC ���ő��
BC = BA �̓ӎO�p�`�̂Ƃ��C
AB ���Œ肵 C �����ƁC��ABC ���ő��
CA = CB �̓ӎO�p�`�̂Ƃ��C
�ł��B���̏�������������B��̏ꍇ�́C��ABC �����O�p�`�̂Ƃ��C�������肦�܂���B
�����ŁC��ABC �̍ő�́C���O�p�`�̂Ƃ��ŁC(��3/4)((��3)r)^2 = (3��3/4)r^2�C�ɂȂ�܂��B
(�l�@)
(��@4)�͂����܂��Ȉ�ۂ���Ǝv���܂��B
�����������(��@3)���������������̂ŁC���Δ����ɋ߂��l������}�`�I�ɏq�ׂ����̂ł��B
��w���x���ɂȂ�܂����C�Δ����ōl���Ă݂܂��傤�B
��AOB = x�C��BOC = y�C�Ƃ��܂��B0 < x, y < 2�C��COA = 2�� - x - y�C�ł��B�����āC
��ABC = ��OAB + ��OBC + ��OCA
= r^2/2 * (sin(x) + sin(y) + sin(2�� - x - y)) = r^2/2 * (sin(x) + sin(y) - sin(x + y))�C
f(x,y) = sin(x) + sin(y) - sin(x + y)�C�Ƃ����ƁC
y ���Œ肵�� x �ŕΔ����Cfx(x,y) = cos(x) - cos(x + y)�C
x ���Œ肵�� y �ŕΔ����Cfy(x,y) = cos(y) - cos(x + y)�C
�ɒl�́Cfx(x,y) = 0 ���� fy(x,y) = 0�C�ŗ^������̂ŁC
cos(x) = cos(y) = cos(x + y)�C
x�Cy �͈̔͂��C
x = y = 2�� - x - y�Cx = y = 2��/3�C��AOB = ��BOC = ��COA =
2��/3�C
�܂�C��ABC �͐��O�p�`�ŁC���̂Ƃ��C(3��3/4)r^2�C�ł��B
�{���́C�Q�K�Δ��������ׂċɑ傩�ǂ����C���E�ōő�┭�U���Ȃ����C�ׂ�̂ł����C
����͐}�`�I�ɂقږ��炩�Ȃ̂ł����ł��傤�B
�����ŁC(��@4)�Ƃ̑Ή�������ƁC
y ���Œ肵�� x �ŕΔ����@�[�[�[�[�[���@BC ���Œ肵 A �����C�ɑΉ��C
x ���Œ肵�� y �ŕΔ����@�[�[�[�[�[���@AB ���Œ肵 C �����C�ɑΉ��C
fx(x,y) = 0�Ccos(x) = cos(x + y)�@�[�[�[�[�[���@AB = AC �̓ӎO�p�`
fy(x,y) = 0�Ccos(y) = cos(x + y)�@�[�[�[�[�[���@CA = CB �̓ӎO�p�`
�ƂȂ��Ă��āC(��@4)�����Δ����ɋ߂���@�ɂȂ��Ă��邱�Ƃ�������܂��B
�Ȃ��C�ȗ����܂����C�������������̎��Ɏ�荞���O�����W���̖���搔�@���g���ƁC
��莮���Ώ̓I�ɔ������Ȃ�C�܂��܂�(��@4)�ɋ߂��Ȃ�܂��B
(���z)
���̖��͖{���I�ɂQ�̎��R�x������肾�Ǝv���܂��B
�����ŁC�Q�̕ϐ��������̂����R�ł��B
�����������́C�������C���R�x���P�̖�������Ȃ�܂��B
�����ł������̍H�v���K�v�ɂȂ�܂��B
�悭�s����̂́C���炩�̊����̕s�����Ɏ������ށC�P��(�ȏ�)�̎��R�x���Œ肵�čl����C�Ȃǂ��Ǝv���܂��B
(��@1)��(��@2)�͑O�ҁC(��@3)��(��@4)�͌�ҁC�ł��傤���B
��҂̋��ɂ̎p����w���x���̕Δ����ƌ��������ł��ˁB
NO2�u�l�c�����v
10/26 15��26���@��M �X�V 11/22
���W�n������D
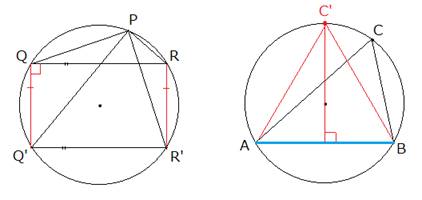
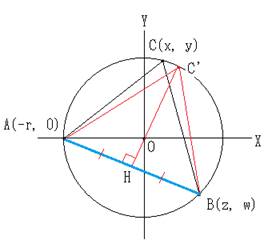
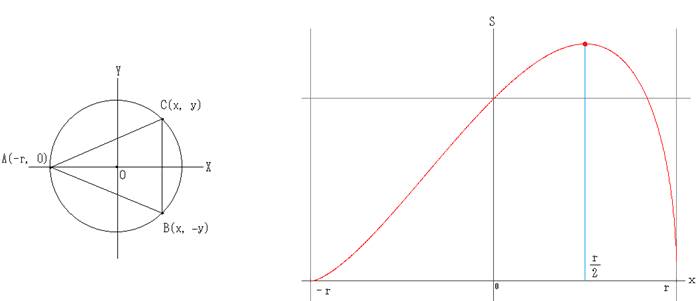
�@���a���̉~�ɓ��ڂ��遢�`�a�b�ɂ����āC
�@�@�`(�O�C��)�C�a(��cos���C��sin��)�C�b(��cos���C��sin��)�i�|�^�Q�������^�Q�j
�Ƃ���D
�@�ʐςr�́C
�@�@�r���P�^�Q�E�b(��cos���|�O)(��sin���|��)�|(��cos���|�O)(��sin���|��)�b
�@�@�@�����Q�^�Q�E�bcos��sin���|cos���|sin��cos���{cos���b
�@�@�@�����Q�^�Q�E�b�|(sin��cos���|cos��sin��)�|(cos���|cos��)�b
�@�@�@�����Q�^�Q�E�bsin(���|��)�{(cos���|cos��)�b
�@��(��)��sin(���|��)�{(cos���|cos��)�i���̊��C���͒萔�j�Ƃ���D
�@�@��'(��)��cos(���|��)�|sin��
�@�@�@�@�@��cos(���|��)�|cos(�^�Q�|��)
�@�@�@�@�@���|�Qsin[{(���|��)�{(�^�Q�|��)}�^�Q]sin[{(���|��)�|(�^�Q�|��)}�^�Q]
�@�@�@�@�@���|�Qsin{(�^�Q�|��)�^�Q}sin{���|(���{�^�Q)�^�Q}
�@�����ŁC�|�^�Q�������^�Q����C�O��(�^�Q�|��)�^�Q���^�Q
�@�@��sin{(�^�Q�|��)�^�Q}���O
i). ��'(��)���O�̂Ƃ��Csin{���|(���{�^�Q)�^�Q}���O
�@����(���{�^�Q)�^�Q�Ƃ���ƁCsin(���|��)���O
�@�@���Q���{�����|�����Q���{�Q�i���͐����j
�@�@���Q���{�{���������Q���{�Q�{��
ii). ��'(��)���O�̂Ƃ��C���l�ɁC
�@�@�Q���{���������Q���{�{��
�@�܂Ƃ߂�ƁC
�@�@���������{���̂Ƃ��C��'(��)���O
�@�@�{���������Q�{���̂Ƃ��C��'(��)���O
�@��(��)�́C�������Q�Ȃ̂ŁC
�@�@�������̂Ƃ��C�ő�
�@�@�����{���̂Ƃ��C�ŏ�
�@�̂Ɂb��(��)�b�́C�������܂��͂����{���̂Ƃ��C�ő�
�@�@��(��)��sin(���|��)�{(cos���|cos��)
�@�@�@�@�@��sin{(���{�^�Q)�^�Q�|��}�{cos{���{�^�Q)�^�Q}�|cos��
�@�@�@�@�@��sin(�^�S�|���^�Q)�{cos(���^�Q�{�^�S)�|cos��
�@�@�@�@�@��sin(�^�S)cos(���^�Q)�|cos(�^�S)sin(���^�Q)
�@�@�@�@�@�@�@�{cos(���^�Q)cos(�^�S)�|sin(���^�Q)sin(�^�S)�|cos��
�@�@�@�@�@����Q�E{cos(���^�Q)�|sin(���^�Q)}�|cos��
�@�@��(�{��)��sin(�{���|��)�{cos(�{��)�|cos��
�@�@�@�@�@�@�@���|��Q�E{cos(���^�Q)�|sin(���^�Q)}�|cos��
�@�@�@�@�@�@�@���|[��Q�E{cos(���^�Q)�|sin(���^�Q)}�{cos��]
�ł���̂ŁC��Q�E{cos(���^�Q)�|sin(���^�Q)}�}cos���̍ő�C�ŏ������߂�悢�D
�@���P(��)����Q�E{cos(���^�Q)�|sin(���^�Q)}�|cos���i���̊��j�Ƃ���ƁC
�@�@���P'(��)����Q�E{�|�P�^�Q�Esin(���^�Q)�|�P�^�Q�Ecos(���^�Q)}�{sin��
�@�@�@�@�@�@��sin���|�P�^��Q�E{sin(���^�Q)�{cos(���^�Q)}
�@����sin(���^�Q)�{cos(���^�Q)�Ƃ���ƁC
�@�@���Q��sin�Q(���^�Q)�{�Qsin(���^�Q)cos(���^�Q)�{cos�Q(���^�Q)
�@�@�@�@���P�{sin��
�@�@�����P'(��)��(���Q�|�P)�|�P�^��Q�E��
�@�@�@�@�@�@�@��{���|�P�^(�Q��Q)}�Q�|�X�^�W
�@�����ŁC
�@�@����sin(���^�Q)�{cos(���^�Q)����Q�Esin(���^�Q�{�^�S)
�@�|�^�Q�������^�Q����C�O�����^�Q�{�^�S���^�Q
�@�@���O��sin(���^�Q�{�^�S)���P
�@�@���O��������Q
�@�O���t���C���P'(��)���O
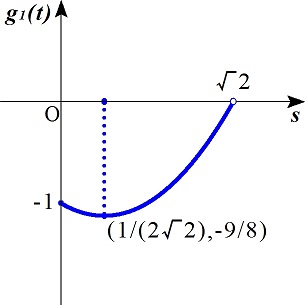
�@�̂ɂ��P(��)�͒P�������ł���D
�@�@���P(�|�^�Q)����Q�E{cos(�^�S)�{sin(�^�S)}�|�O���Q
�@�@���P(�^�Q)����Q�E{cos(�^�S)�|sin(�^�S)}�|�O���O
�ł���C�|�^�Q�������^�Q�ł��邩��C
�@�@�O�����P(��)���Q
�@���Q(��)����Q�E{cos(���^�Q)�|sin(���^�Q)}�{cos���i���̊��j�Ƃ���ƁC
�@�@���Q'(��)����Q�E{�|�P�^�Q�Esin(���^�Q)�|�P�^�Q�Ecos(���^�Q)}�|sin��
�@�@�@�@�@�@���|sin���|�P�^��Q�E{sin(���^�Q)�{cos(���^�Q)}
�@�@�@�@�@�@���|(���Q�|�P)�|�P�^��Q�E��
�@�@�@�@�@�@���|{���{�P�^(�Q��Q)}�Q�{�X�^�W
�@���Q'(��)���O�Ƃ���ƁC
�@�@���{�P�^(�Q��)���}�R�^(�Q��Q)
�@�@�������P�^��Q�C�|��Q
�@�O��������Q����C�����P�^��Q
�@�@��������Qsin(���^�Q�{�^�S)���P�^��Q
�@�@��sin(���^�Q�{�^�S)���P�^�Q
�@�O�����^�Q�{�^�S���^�Q����C���^�Q�{�^�S���^�U
�@�@�������|�^�U
�@�O�����^�Q�{�^�S���^�Q�͈̔͂ŁC������Qsin(���^�Q�{�^�S)�͒P�������D
�@�O���t����C
�@�@�|�^�Q�������|�^�U�ŁC�O�������P�^��Q�ƂȂ�C���Q'(��)���O
�@�@�|�^�U�������^�Q�ŁC�P�^��Q��������Q�ƂȂ�C���Q'(��)���O
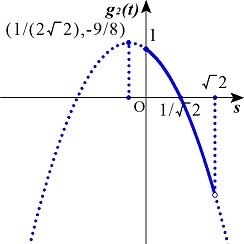
�@�@���Q(�|�^�Q)���Q
�@�@���Q(�^�Q)���O
�@�@���Q(�|�^�U)����Q{cos(�^�P�Q)�{sin(�^�P�Q)}�{cos(�^�U)
�@�@�@�@�@�@�@�@�@���Qsin(�^�P�Q�{�^�S)�{cos(�^�U)
�@�@�@�@�@�@�@�@�@���Qsin(�^�R)�{cos(�E�U)
�@�@�@�@�@�@�@�@�@����R�{��R�^�Q���R�^�Q�E��R
�Ȃ̂ŁC�O�����Q(��)���R�^�Q�E��R
�@�̂Ɂb��(��)�b�̍ő�l�C
�@�@���Ȃ킿�b��(��)�b�C�b��(�{��)�b�̍ő�l�C
�@�@���Ȃ킿�b���P(��)�b�C�b���Q(��)�b�̍ő�l�́C
�����|�^�U�̂Ƃ��C�R�^�Q�E��R
�@���̂Ƃ��C
�@�@�����{�����{(���{�^�Q)�^�Q���{(�|�^�U�{�^�Q)�^�Q���V�^�U�E��
�@�̂ɂr�̍ő�l�́C
�@�@���Q�^�Q�E�R�^�Q�E��R��(�R��R)�^�S�E���Q
�@���̂Ƃ��C
�@�@�`(�O�C��)�C�a(��cos(�V�^�U�E��)�C��sin(�V�^�U�E��))�C�b(��cos(�|�^�U)�C��sin(�|�^�U))
�@����́��`�a�b���P�ӂ̒�������R�E���̐��O�p�`�ł��邱�Ƃ�\��
�u�l�c�����v
10/27 16��04���@��M �X�V 11/22
�i�ʉ��j�i�O��͓ӎO�p�`�ł��邱�Ƃ��g�킸�ɉ����܂������C����͎g���ĉ����܂��D����������͋��ȏ��̉��K��背�x���ŁC�������ۂɎ��Ƃʼn�����܂����j
�@���`�a�b���C���a���̉~�ɓ��ڂ���Ƃ��āC
�@�@�a(�|���C�|(���Q�|���Q)�P�^�Q)�C�b(���C�|(���Q�|���Q)�P�^�Q)�i�O���������j
�Ƃ���D
�@�a�b���ӂƂ����Ƃ��̍������ő�̂Ƃ��ɁC�ʐςr���ő�ƂȂ�D
�@�̂ɂ`(�O�C��)�Ƃ���悢�D
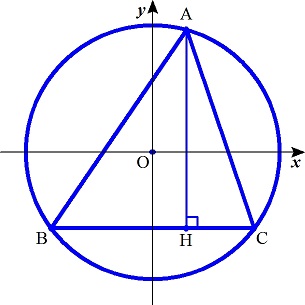
�@���̂Ƃ��C
�@�@�r���P�^�Q�E�Q���E{���{(���Q�|���Q)�P�^�Q}
�@�@�@����{���{(���Q�|���Q)�P�^�Q}
�@�@���r'��{���{(���Q�|���Q)�P�^�Q}�{���E(�|�Q��)�^{�Q(���Q�|���Q)�P�^�Q}
�@�@�@�@��{��(���Q�|���Q)�P�^�Q�{(���Q�|���Q)�|���Q}�^(���Q�|���Q)�P�^�Q
�@�@�@�@��{��(���Q�|���Q)�P�^�Q�|(�Q���Q�|���Q)}�^(���Q�|���Q)�P�^�Q
�@�����ŁC������(���Q�|���Q)�P�^�Q�Ƃ����Q���Q�|���Q�i�O���������j�̃O���t���l����D
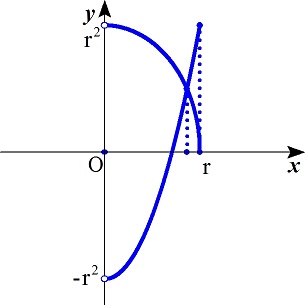
�@���L�_�̂����W�����߂�D
�@��(���Q�|���Q)�P�^�Q���Q���Q�|���Q�Ƃ���ƁC
�@�@���Q(���Q�|���Q)��(�Q���Q�|���Q)�Q
�@�@�����S�|���Q���Q���S���S�|�S���Q���Q�{���S
�@�@���S���S�|�R���Q���Q���O
�@�@���S���Q(���Q�|�R�^�S�E���Q)���O
�@�@�������O�C�}��R�^�Q�E��
�@�O���t���C������R�^�Q�E��
�@�O��������R�^�Q�E���̂Ƃ��C��(���Q�|���Q)�P�^�Q���Q���Q�|���Q�ƂȂ�C�r'���O
�@��R�^�Q�E�����������̂Ƃ��C��(���Q�|���Q)�P�^�Q���Q���Q�|���Q�ƂȂ�C�r'���O
�@�̂ɂr�͂�����R�^�Q�E���̂Ƃ��C�ő�ƂȂ�C�ő�l�́C
�@�@��R�^�Q�E���E{���{(���Q�|�R�^�S�E���Q)�P�^�Q}����R�^�Q�E���E(���{���^�Q)��(�R��R)�^�S�E���Q
�@���̂Ƃ��C�a(�|��R�^�Q�E���C�|���^�Q)�C�b(��R�^�Q�E���C�|���^�Q)
�@�܂聢�`�a�b�͂P�ӂ̒�������R�E���̐��O�p�`�ƂȂ�D
�i�ʉ����̂Q�j
�@�`(�O�C��)�C�a(��cos��,��sin��)�C�b(�|��cos�ƁC��sin��)�i���Ɓ��R�^�Q�E�j�Ƃ���ƁC
�@�@�r���P�^�Q�E(�|�Q��cos��)�E(���|��sin��)
�@�@�@�����Qcos��(sin�Ɓ|�P)
�@�@���r'�����Q�E{�|sin��(sin�Ɓ|�P)�{cos�ƁEcos��}
�@�@�@�@���|���Q{sin��(sin�Ɓ|�P)�|(�P�|sin�Q��)}
�@�@�@�@���|���Q(sin�Ɓ|�P){sin�Ɓ{(�P�{sin��)}
�@�@�@�@���|���Q(sin�Ɓ|�P)(�Qsin�Ɓ{�P)
�@���Ɓ��R�^�Q�E�Ȃ̂ŁC
�@�@���Ɓ��V�^�U�E�̂Ƃ��C�r'���O
�@�@�V�^�U�E���Ɓ��R�^�Q�E�̂Ƃ��C�r'���O
�@�̂ɂr�̓Ɓ��V�^�U�E�̂Ƃ��C�ő�ƂȂ�D�@�@�@�E�E�E
�u�l�c�����v
10/29 10��26���@��M �X�V 11/22
�i�ʉ����̂R�j
�@�`(�O�C��)�C�a(�|���C�|��)�C�b(���C�|��)�i�O���������C�O���������C���Q�{���Q�����Q�j�C�r�����`�a�b�Ƃ���ƁC
�@�@�r���P�^�Q�E�Q���E(���{��)����(���{��)
�@�@���r�Q�����Q(���{��)�Q��(���Q�|���Q)(���Q�{�Q�����{���Q)�����S�{�Q���R���|�Q�����R�|���S
�@���̎�����(��)�Ƃ���ƁC
�@�@��'(��)���Q���R�|�U�����Q�|�S���R���|�Q(�Q���R�{�R�����Q�|���R)
�@�@�@�@�@���|�Q���R(�Q�w�R�{�R�w�Q�|�P)
�@�������C�w�����^���C�O���w���P
�@�@����'(��)���|�Q���R(�w�{�P)(�Q�w�Q�{�w�|�P)���|�Q���R(�w�{�P)�Q(�Q�w�|�P)
�@�O���w���P�^�Q�C���Ȃ킿�O���������^�Q�̂Ƃ��C��'(��)���O
�@�P�^�Q���w���P�C���Ȃ킿���^�Q���������̂Ƃ��C��'(��)���O
�@�̂ɂ�(��)���r�Q�́C�������^�Q�̂Ƃ��C�ő�ƂȂ�C�r���ő�ƂȂ�D
�@���̂Ƃ��r�̍ő�l�́C����{���Q�|(���^�Q)�Q}�P�^�Q����R�^�Q�E������C
�@�@��R�^�Q�E���E(���{���^�Q)��(�R��R)�^�S�E���Q
�@�܂��C�a(�|��R�^�Q�E���C�|���^�Q)�C�b(��R�^�Q�E���C�|���^�Q)�ƂȂ�̂ŁC���`�a�b�͐��O�p�`�ł���D
NO3�u�ɂ���Z12�v 10/27 02��18���@��M
�X�V 11/22
�C�ӂɔ��a���̉~�ɓ��ڂ���O�p�`S�iS�F�O�p�`�̖��̂ƎO�p�`�̖ʐςɓ��L����p���܂��j�̒��_�Ɏ��̕�����U��܂�
�O�p�`�̂����ꂩ�̒��_��A�Ƃ������v����ABC
��BC�ƒ�ӂƂ��i���₷�����邽�߁jBC���iB����C���E�j�����ƂȂ�悤��ABC���~���ʼn�]���܂��i��]�ɂ��ʐς̕ϓ��͂���܂���j
A����BC�ɐ����̑������낵���̒��������Ƃ��܂�
��ABC�̖ʐς�BC�~����2�E�E�E�@
���̎�BC��ς���A�a���̉~�ɉ����ē������_�ƍl�����
���̍ő�l�͉~�̒��S��ʂ�܂�
���̎��̂���h�f�Ƃ��܂��B���̎��̎O�p�`��S�f�Ƃ��܂��B
�܂����̎�
h <h�f
AB=AC
��������̂�
�@����
S��S�f
�������܂��B
���̂��Ƃ́A
�~�ɓ��ڂ���3�p�`��ӂ��Œ肵�A�c�钸�_�_�Ƃ����Ƃ��ɖʐς��ő�ƂȂ�Ƃ����Y�O�p�`�͌Œ肵���ӂ��ӂƂ���2���ӎO�p�`�ƂȂ�B
�Ɠ��l�ł�
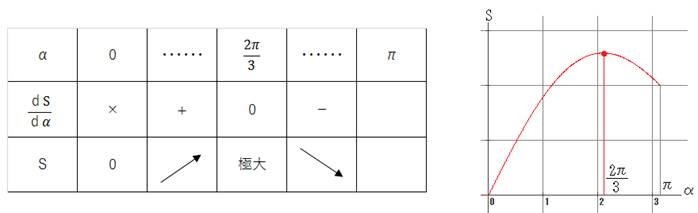
���ɁAh�f��BC��ω������܂��i�ω�������h�f��BC��h�f�f��BC�f�A�ω��������O�p�`��S�f�f�Ƃ��܂��j
���a���̉~�̒��S��O�Ƃ��܂�
OB�AOC���������i��͓I�ɂ͂����j�ƂȂ��p���ƂƂ����
BC=2��cos��
h�f����+��sin��
h�f�̒l��́A0�� h�f�f ��2r
�]����
S�f ��(2��cos��)(��+��sin��)/2
�����ŁAh�f��BC��ω�������ƃƂ��ω�����̂ł�������f�Ƃ����
S�f�f ��(2��cos���f)(��+��sin���f)/2�E�E�E�A
�ƂȂ�܂�
�܂�
h�f����+��sin���f
h�f�̒l��́A0�� h�f�f ��2r
���f�̒�`���0�����f����/2
����������
S�f�f ����2(cos���f)(1+sin���f)=r2(cos���f+(1/2)sin(2���f))
���̋ɒl�́i�[�܂�܂����j
�E�ӂ����f�Ŕ�������0�ƒu�����܂�܂��B
���ʂ�
-2sin2���f-sin���f+1=0
sin���f=1/2,-1
0�����f����/2���
���f=��/6
���̑����\������f=��/6��S�f�f�̍ő�l��^���鎖������܂�
|
���f |
0 |
��/6 |
��/2 |
|
-2sin2�Ɓf-sin�Ɓf+1 |
+1 |
0 |
-2 |
����āA
S�f��S�f�f
�������܂��B
�Ƃ���ŁA���f=��/6
�Ȃ�ӎO�p�`��
��ABC=��ACB=��BAC����/3
�ƂȂ�̂�
S�f�f�͐��O�p�`�ƂȂ�܂�
���̂��Ƃ�
��ӂ������Ɏ�����Ƃ��Ă��iAB,BC,AC�̑Ώ̐�����j���l�ȋc�_�����藧���܂��B
�����
S��S�f��S�f�f
�͏�Ɍ����A���ar�̉~�ɓ��ڂ��鐳�O�p�`S�f�f�͂��ׂč����ł�
�]���Ĕ��a���̉~�ɓ��ڂ���O�p�`�̖ʐς̍ő�l�͐��O�p�`S�f�f��
���f=��/6
S�f�f ����2(cos���f)(1+sin���f)��r23��3/4�E�E�E��
�u�ɂ���Z12�v 11/09 02��17���@��M
�X�V 11/22
���͎��̂悤�ɏ��������܂�
�E�O�p�`�̊O�S����e���_(ABC)�܂ł̋��������ł���O�p�`S(S�͓��ɒf��Ȃ�����O�p�`�ƎO�p�`�̖ʐς̗����̕\�L�Ɏg�p���܂�)�����ʐς̍ő�l�����߁A���̎O�p�`�����O�p�`�ł��邱�Ƃ������Ȃ����B
����
�@S�̊O�S��O�Ƃ��܂��B�܂�
�@��AOB=��1
��AOC=��2
��BOC=��3=2��-��1-��2
�@
S��r�Er sin(��1)+ r�Er sin(��2)
+ r�Er sin(��3)
��r2
(sin(��1)+ sin(��2) + sin(2��-��1-��2))
��r2 (sin(��1)+
sin(��2) - sin(��1+��2))
S/ r2��sin(��1)+
sin(��2) - sin(��1+��2)
��sin(��1)+
sin(��2) - sin(��1) cos(��2) - cos (��1) sin (��2)
�E�E�E���@�藝
��sin(��1)(1-
cos(��2) )+ sin(��2) (1- cos(��1) )
S/ r2��sin(��1)(1-
(1- sin (��2))^0.5)+ sin(��2) (1- (1- sin (��1))^0.5)
�E�E�E�E�E�E�E�@
r2�͏퐔�Ȃ̂�S���ő�l�����͉̂E�ӂ��ő�l�����Ƃ��ł�
�悸�ʐς��ő�ƂȂ�O�p�`���̈�ӂ��O�S��ʂ�Ȃ����Ƃ��ؖ����܂��B�i�O�S���O�p�`�̓����ɂ��邱�Ƌy�у�123����菬�������Ɓj
��ӂ��O�S��ʂ�O�p�`�̖ʐς�
�O�S��ʂ�Ӂi2���j�~�����i���j�^2�ł����Ah�̍ő�l�͂��ƂȂ邱�Ƃ͎����ł��B���������Ă��̖ʐς͂�2�͂ƂȂ�܂�
�O�S��ʂ�ӈȊO�̕ӂ��ӂƂ��Ή����钸�_���ړ�����Ɩ��炩�ɎO�p�`�̖ʐς͂�2���傫���Ȃ�B
�i��ӈ��ɑ������͍����Ȃ�j
�����z�͊O�S��ʂ�Ȃ��B
���l�ɂ��āA�O�S������Ɋ܂܂Ȃ��O�S�����̎O�p�`�͊O�S�����̎O�p�`�̍ő�ʐς̎O�p�`�ł͂Ȃ��B
�@�@�E�E�E�E�iA�j
�����@�ɂ����Ď��̂悤�ɒu�����������܂�
z= S/ r2
x= sin(��1)�@��`��i0<x<1�j
y= sin(��2) ��`��i0<y<1�j
z= x(1-(1-y2)^0.5)+y(1-(1-x2)^0.5�E�E�E�E�E�E�E�A
�E�ӂ�x��y�̑Ώ̎��ƂȂ��Ă��܂�
����́A���������W�ɂ����āA�Ȗʂ��Ɛ���x=c�Ƃ̌����y�����ʂւ̎ʑ��Ɛ���y=c�Ƃ̌����x�����ʂւ̎ʑ�������ƂȂ邱�Ƃ��Ӗ����܂��B(0<c<1:�C�ӏ퐔)�E�E�E�i�A�j
����ɁA�Ȗʂ��Ɛ���x=c�Ƃ̌����y�����ʂւ̎ʑ�
�@z= c(1-(1-y2)^0.5)+y(1-(1-c2)^0.5
�͂���1�̋ɒl�i�ő�l�j�������܂��B(y�Ŕ�����0�ƒu���ƒ�`����1�̉������Ȃ�)�E�E�E�E�E�i�C�j
�]����z�̋ɒl�͐���x=y�ƋȖ�z�̌����ɂ���܂��E�E�E�E�E�iB�j
�s�i�C�j�������Ă����Ȃ���B���������܂���B����Ƃ��āA�Ȗʂ��Q���ԃ��N�_�̏ꍇ������܂��t
B����A��y=x�������ɒl�����߂܂��B
z= 2x(1-(1- x2)^0.5)
dz/dx= d(2x(1-(1- x2)^0.5))/dx=0
1-(1- x2)^0.5+ x2/(1- x2)^0.5=0
x=�}3^0.5/2
x�̒�`�悩��
x=3^0.5/2
����Ă����ɒl�i�ő�l�j�����Ƃ��̂��A���͂���������3/2�ƂȂ�܂��B
��`�悩���1��2�̓�/3��2��/3���Ƃ�܂���
A���
��1��2�̑g�ݍ��킹��
��/3+��/3�E�E�E�O�p�`�̓����ɊO�S���܂܂Ȃ��~
��/3+2��/3�E�E�E�O�p�`��1�ӂ��O�S��ʂ�~
2��/3+��/3�E�E�E�O�p�`��1�ӂ��O�S��ʂ�~
2��/3+2��/3�E�E�E�O�p�`�̓����ɊO�S���܂ށ�
����
��1����2��2��/3
�ƂȂ�
��3��2��-(��1+��2)��2��/3����1����2
�Ȃ̂�
���߂�O�p�`��
���O�p�`�ŁE�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E��1
���̖ʐς�
3�ir�~r�Esin�i2��/3�j�j��3�~��2��3/2��3��3/2��2�E�E�E�E�E�E��2
�ƂȂ�܂��B
NO4�u���N���̂�������v 10/27 17��07���@��M �X�V 11/22
�������͐��O�p�`�̂Ƃ��Ȃ̂ŁA![]() �ł��B
�ł��B
���~�ɓ��ڂ���O�p�`�ŁA��ӂ��Œ肵���Ƃ��A�ʐς̍ő�́A���̕ӂ��ӂƂ���ӎO�p�`�ł��B
���̂��Ƃ����Ƃɂ��āA�l���Ă݂܂��B
�s�p�O�p�`��7�͂��߂ɍl���܂��B
�~�ɓ��ڂ���O�p�`�ŁA�݊p�O�p�`�����傫�ȉs�p�O�p�`������͖̂��炩������ł��B
���̐}�ŁA��PQR����PQ�fR�f�ł��B
�E�̐}�́A��ABC�̕�AB���Œ肵�A���_C��AB�̐���������Ɉړ��������̂ł��B
���̂Ƃ��A��ABC����ABC�f�ł��B
�Ȃ��Ȃ�A�O�p�`�̖ʐς������ɔ�Ⴗ�邩��ł��B
�E�̐}�ŁAAB=c �ABC=a �ACA��b �Ƃ��Ab��c��a�Ƃ��܂��B
�܂�A�Œ肷��ӂ��܂̒����̂��̂Ƃ��܂��B
BC�f��a�f �AC�fA��b�f �Ƃ���A
�E��C��60���̂Ƃ��́Ab���ib�f��a�f�j��c�@�@�@�@�@ ��a
�E��C��60���̂Ƃ��́Ab���@�@�@�@ c���ib�f��a�f�j��a
�ƂȂ�܂��B
���܂ň�Ԓ��������ӂ͒Z���Ȃ�A��ԒZ�������ӂ͒����Ȃ�A���������̓�����������ɂȂ�܂��B
���̌��ʁA���܂ł��3�ӂ̕����������Ȃ�܂����B
�O�p�`�̏ꍇ�A�ӂ̒����̑召�A�Ίp�̑召�͈�v���܂��B
b��c��a�Ȃ�AB��C��A�ł��B
���Ƃ��A�E�̐}�Ł�C��60���Ƃ���ƁAC>A�f��B�f�ƂȂ�܂��B
������Ac��b�f��a�f�ƂȂ�܂��B
���̒i�K�ɂ���܂��B
�ӎO�p�`�̓�������ӂ̂�����BC�f���Œ肵�ē��l�̂��Ƃ��J��Ԃ��܂��B
����ƁA�܂�3�ӂ̕����������Ȃ�̂ŁA�܂��܂����O�p�`�ɋ߂Â��Ă����܂��B
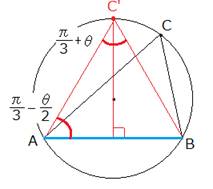 �p�ł��̗l�q�����Ă݂܂��B
�p�ł��̗l�q�����Ă݂܂��B
�͂��߂́�C�̑傫���� ![]() �Ƃ��܂��B
�Ƃ��܂��B
����ƁA1��ڂ̓ӎO�p�`�̒�pA�f�́AA�f![]() �ƂȂ�܂��B
�ƂȂ�܂��B
�܂�A���O�p�`�� ![]() �ɑ��Ĕ��[�Ȋp�������Ⴂ�Ŕ����ɂȂ�܂��B
�ɑ��Ĕ��[�Ȋp�������Ⴂ�Ŕ����ɂȂ�܂��B
���̑��������s���ƓӎO�p�`�̒�p��![]() �ƂȂ�܂��B
�ƂȂ�܂��B
�p���ǂ�ǂ����Ȃ�A���O�p�`�ɋ߂Â��Ă������Ƃ��킩��܂��B
����2�̒��S�p��ϐ��Ƃ��āA��ӂ��Œ肷��ƁA�ӎO�p�`�̂Ƃ��ő�ł��邱�Ƃ������܂��B
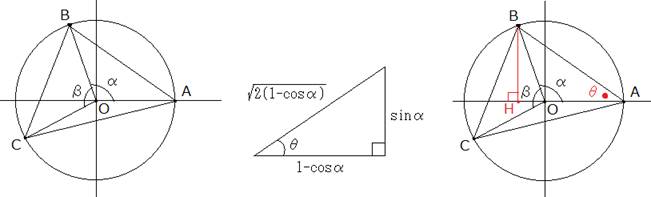
���̐}�̂悤�ɁA�~�ɓ��ڂ���O�p�`�Ł�AOB�����A��BOC�����Ƃ����܂��B
�O�p�`�̖ʐς�S�Ƃ����ƁA���̂悤�ɕό`�ł��܂��B
�����Œ肵�A���ŎO�p�����������Ă����܂��B
![]()
![]()
![]()
�Ƃ͂܂̐}�̂悤�ȎO�p�`�̓��p�ł��B
�E�̐}�ŁA![]() �A
�A![]() �Ȃ̂ŁA�Ƃ́�OAB�ɓ������Ȃ�܂��B
�Ȃ̂ŁA�Ƃ́�OAB�ɓ������Ȃ�܂��B
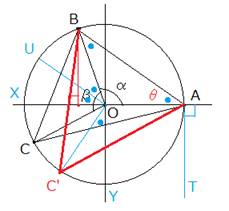
![]() �́A�����Œ肷��ƁA
�́A�����Œ肷��ƁA![]() �̂Ƃ��A�ő�l���Ƃ�܂��B
�̂Ƃ��A�ő�l���Ƃ�܂��B
�܂�A![]() �ł��B
�ł��B
���āA (��)���A������BAT�ł��B
��OAB�͓ӎO�p�`�Ȃ̂ŁA��O�̊O�p�̓���OU��AB�ƕ��s�ł��B
��BAT����UOY�Ȃ̂ŁAC�f�̈ʒu�́AY�̈ʒu����Ƃ��ǂ����Ƃ���ł��B
����ƁA![]() �ƂȂ�A��C�fAB�͓ӎO�p�`�ɂȂ�܂��B
�ƂȂ�A��C�fAB�͓ӎO�p�`�ɂȂ�܂��B
![]() �́A�����Œ肷��ƁA
�́A�����Œ肷��ƁA![]() �̂Ƃ��A�ő�l���Ƃ�܂��B
�̂Ƃ��A�ő�l���Ƃ�܂��B
�܂�A![]() �ł��B
�ł��B
���āA (��)���A������BAT�ł��B
��OAB�͓ӎO�p�`�Ȃ̂ŁA��O�̊O�p�̓���OU��AB�ƕ��s�ł��B
��BAT����UOY�Ȃ̂ŁAC�f�̈ʒu�́AY�̈ʒu����Ƃ��ǂ����Ƃ���ł��B
����ƁA![]() �ƂȂ�A��C�fAB�͓ӎO�p�`�ɂȂ�܂��B
�ƂȂ�A��C�fAB�͓ӎO�p�`�ɂȂ�܂��B
�ȏォ��A��ABC�Ń����Œ肷��ƁA�ʐς̍ő�́A���_C���ӎO�p�`�̈ʒu�ł��B
 ��������œӎO�p�`�̂Ƃ��ʐύő傪�������̂ŁA1�ϐ��ōl���܂��B
��������œӎO�p�`�̂Ƃ��ʐύő傪�������̂ŁA1�ϐ��ōl���܂��B
�ӎO�p�`��ABC�̒��_A�̒��S�p�����Ƃ��܂��B
![]()
![]()
![]()
![]()
![]()
![]()
�����ŁA![]() �̂Ƃ��A
�̂Ƃ��A![]() �Ȃ̂ŁA
�Ȃ̂ŁA![]() �̂Ƃ��A
�̂Ƃ��A![]() �ł��B
�ł��B
![]() �������āA
�������āA![]()
 �������x��2�̒��_�̂����W��ϐ��Ƃ��čl���܂��B
�������x��2�̒��_�̂����W��ϐ��Ƃ��čl���܂��B
�}�̂悤�Ɍ��_���S�A���ar�̉~�����
3�_A�AB�AC���Ƃ�܂��B
��̂��߂ɂ��͐��A���͕��Ƃ��Ă����܂��B
![]() �A
�A![]() �Ȃ̂ŁA��ABC�̖ʐ�S�́A
�Ȃ̂ŁA��ABC�̖ʐ�S�́A
![]() �ł��B
�ł��B
![]() �Ȃ̂ŁA
�Ȃ̂ŁA
![]() �ł��B
�ł��B
�����ŁA��AB���Œ肵�Ėʐς̑����ׂ܂��B
![]() �ł��B
�ł��B
S�f=0���A
![]()
���̗��ӂ�2�悵�āA![]()
![]() ���A
���A![]() �𐳂Ƃ��āA
�𐳂Ƃ��āA![]() ������(����)
������(����)
![]() �A
�A![]() �Ȃ̂ŁA��ABC�̖ʐ�S�́A
�Ȃ̂ŁA��ABC�̖ʐ�S�́A
![]() �ł��B
�ł��B
![]() �Ȃ̂ŁA
�Ȃ̂ŁA
![]() �ł��B
�ł��B
�����ŁA��AB���Œ肵�Ėʐς̑����ׂ܂��B
![]() �ł��B
�ł��B
S�f=0���A
![]()
���̗��ӂ�2�悵�āA![]()
![]() ���A
���A![]() �𐳂Ƃ��āA
�𐳂Ƃ��āA![]() ������(����)
������(����)
�����ŁAAB�̐��������Ɖ~�Ƃ̌�_�ɂ��Ē��ׂ܂��B
AB�̌X���́A![]() �Ȃ̂ŁA�����ȌX���́A
�Ȃ̂ŁA�����ȌX���́A![]() �ł��B
�ł��B
�������������_��ʂ�͖̂��炩�Ȃ̂ŁA�~�ƘA�������āA
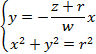
![]()
![]()
![]()
![]()
![]() ���A
���A![]() �𐳂Ƃ��āA
�𐳂Ƃ��āA![]()
���̌��ʂ́A(����)�Ɠ����ł��B
�܂�A�ʐς̋ɒl��^����![]() �ƓӎO�p�`�ɂȂ�
�ƓӎO�p�`�ɂȂ�![]() �Ƃ���v����Ƃ������Ƃł��B
�Ƃ���v����Ƃ������Ƃł��B
��������ŁA�ӎO�p�`�̂Ƃ��ʐύő傪�킩�����̂ŁA1�ϐ��ōl���܂��B
���̐}�̂悤�ɓӎO�p�`�������܂��B
����ƁA�ʐ�S�́A
![]()
![]()
![]() �Ƃ��āA
�Ƃ��āA![]()
���̐��藧������![]() �ŋɑ�l���Ƃ�͖̂��炩�Ȃ̂ŁAS�̎��ɑ������ƁA
�ŋɑ�l���Ƃ�͖̂��炩�Ȃ̂ŁAS�̎��ɑ������ƁA
![]()
NO5�u��x�Ђ����v 11/16 20��44���@��M
�X�V 11/22
(��)���ar�̉~�ɓ��ڂ���O�p�`�̖ʐς̍ő�l�� ((3��3)/4)*r^2�@�ł���D
(�ؖ�)
�ȉ��ł́C��ABC�̖ʐς� |��ABC| �Ƃ����ӂ��ɏ������̂Ƃ���D
���ar�̉~�ɓ��ڂ��鐳�O�p�`�̖ʐς� ((3��3)/4)*r^2 �ł���C
���̒l�� S �Ƃ���D
��ABC���C���ar�̉~�ɓ��ڂ��C�Ȃ����C���O�p�`�ł͂Ȃ�
�悤�ȔC�ӂ̎O�p�`�Ƃ���D
���܂��� |��ABC|��S �ł��邱�Ƃ������D
��ABC�͐��O�p�`�ł͂Ȃ��̂ł��邩��C��ABC��60������
���������p�ƁC60�������傫�����p�Ƃ������Ă���D
��ABC��60���C��ACB��60���Ƃ��Ă���ʐ�������Ȃ��D
����BC�̐��������Ɋւ��āCA�ƑΏ̂ȓ_��D�Ƃ���D
��DBC=��ACB��60���D
��AD(B�CC �����̏�ɏ���Ă��Ȃ����̌�)��ɓ_E���Ƃ��āC
��EBC=60��
�ƂȂ�悤�ɂł���D
E�͌�AD��ɂ����āCE��A�CE��D�ł��邩��C
|��EBC|��|��ABC| ------ (��) �����藧���Ă���D
��CE(B�����̏�ɏ���Ă�����̌�)�̒��_��M�Ƃ���D
|��EMC|��|��EBC| ------ (��) �����藧���Ă���D
��EMC=��EBC=60���CME=MC �ł��邩��C
��EMC�͐��O�p�`�ł���D
����āC|��EMC|=S�D
(��)���CS��|��EBC|�D
(��)�Ƃ���C|��ABC|��S�D
�@
�ȏ���C���ar�̉~�ɓ��ڂ���O�p�`�̖ʐς̍ő�l��S�ł���
�ƌ��_�ł���D(�ؖ��I)
NO6�u�W���[�J�[�v�@�ߘa3�N�i2021�j 03/30 11��05���@��M
�X�V�@�ߘa3�N3/31
�@�@�u�W���[�J�[�v�@�ߘa3�N�i2021�j 03/31 23��58���@��M �X�V�@�ߘa3�N4/1
�ߘa3�N�i2021�N�j�Ɋ�ꂽ�W���[�J�[�����̉����B
�����̗���F�Δ����̗��p�őf���������Ă��܂��B��
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
