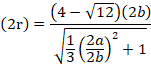令和２年１１月２９日
[流れ星]
第393回数学的な連続応募解答
＜解答募集期間：11月1日〜11月29日＞
［朝倉真禅院奉納算額１］
岐阜県垂井町にある真禅院 三重の塔（国重要文化財）
江戸時代末期、谷松茂（幽斎）は大垣藩士で致道館講官であった水野民興に学び、自ら塾を開いて和算を教えていました。
彼の門人達が天保12年（1841）に亡くなれた谷幽斎先生を偲んで垂井町宮代の南宮大社に弘化2年（1845）に奉納算額二編を奉納しています。
この算額は残念ながらと紛失したことを知り、奉納された算額は復元をし、後世に残しておきたいと熱望した次第です。
以下の奉納された問題の解法をお願いします。応募解答は後日、奉納算額の解答冊子に利用させていただきます。
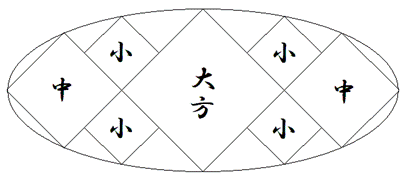
第２問題
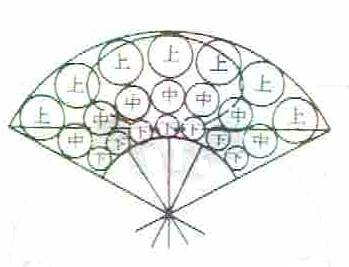
楕円の内に平行な弦を作り図のように、楕円と平行な弦に接する４個の乾円と4個の坤円を入れる。このとき、楕円の長径と短径を知って、乾円が最小となるときの坤円の直径を求めよ。 11月10日 一部補足・訂正
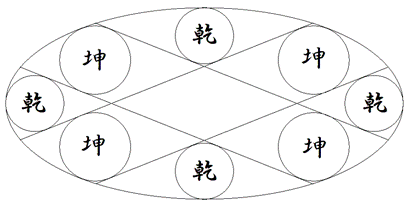
術文（答）について
図において，扇面ACB−A1DB1の面積をSとすると，
↓
楕円の長径を2a，上円の直径を2r，扇面の面積をSとすると，
赤字は補足11月9日
したがって、今まであった図４は削除します。
「ジョーカー」
11/14 14時01分 受信 更新 11/29
「よふかしのつらいおじさん」 11/22 16時56分 受信
更新 11/29
第1問題
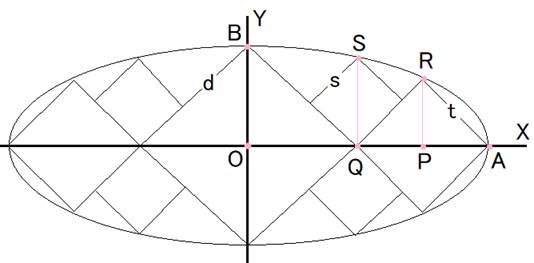
●図のように符号を付けます。
正方形の1辺を大：d、中：t、小：sとします。
なので、楕円の方程式は、
です。
でないと中が正方形になりません。
よって、
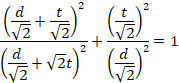
整理すると、
t＞0なので、
これを楕円の方程式に代入します。
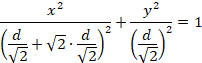
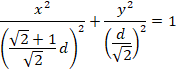
●QSの長さを調べます。
なので、
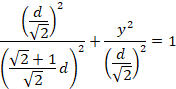
より、
よって、小の正方形の1辺の長さsは、
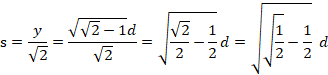
第2問題
●楕円の方程式を、
右の乾の方程式を、
上の乾の方程式を、
接線pを、
接線qを、
とします。
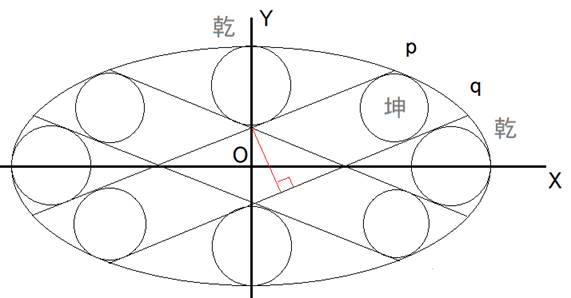
●右の乾の中心はa−r、上の乾の中心はb−rです。
右の乾の中心からqまでの距離、上の乾からpまでの距離はともにrなので、
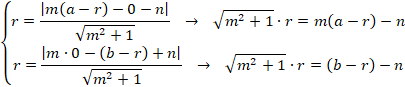
連立させると、
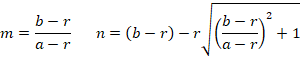
よって、接線qは、
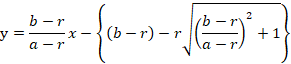
●接線pとqの距離を調べます。
この値が坤の直径になります。
pのy切片(0，n) からq（
）までの距離dは、
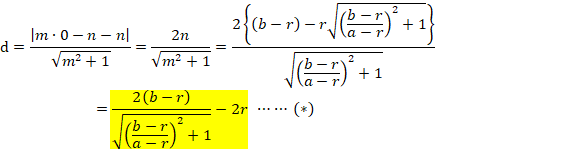
●ここで、右の乾が楕円の中に入ることを調べます。
上の乾は楕円が横長なので問題ありません。
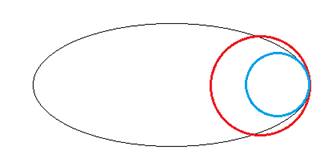
楕円の方程式は、
右の乾の方程式は、
(**)を楕円の式に入れて整理すると、
判別式は、
判別式が正だと上の図の赤の状態です。
この判別式は負にはならないので0のときが乾の最大です。
このとき、
●この値を直線p、qの間隔dの式(*)に代入すると、
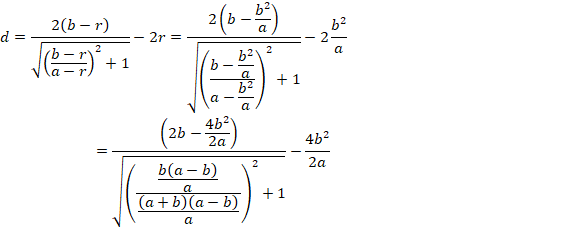
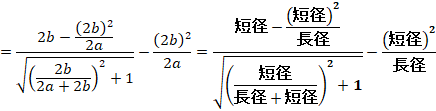
第3問題
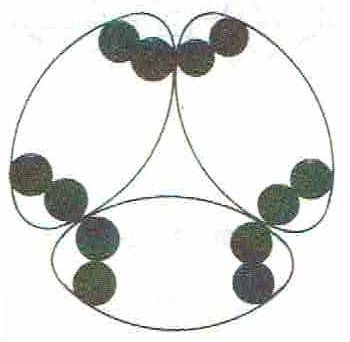
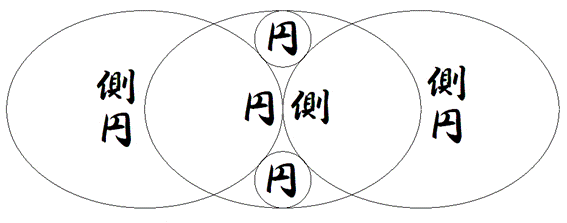
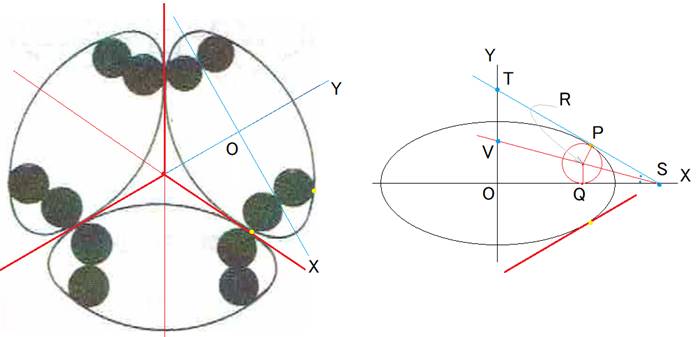
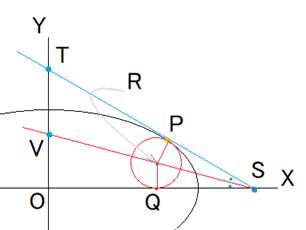
●左の図のように補助線を引くと、1つの楕円は120°の範囲に入ります。
右の図で赤の接線の傾きは
です。（青の方は
）
楕円の方程式を、接点Pの座標を
、円の半径をrとします。
●楕円の点Pでの接線は、
です。
x軸との交点は
、y軸との交点は
楕円の方程式をxで微分し、y' を求めます。
接点の座標を求めます。
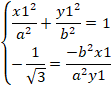
連立させて、
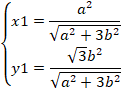
S、Tをa、bで表すと、
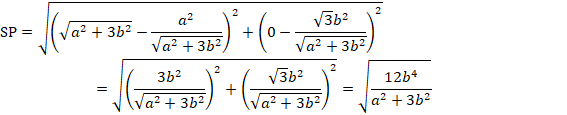
●SVは∠OSTの2等分線なので、中線定理から
△SRQ ∽ △SVO です。
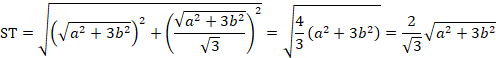
よって、
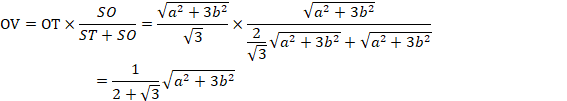
SQ=SPです。
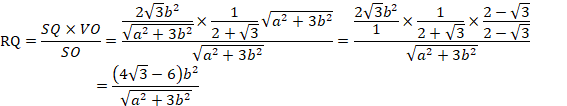
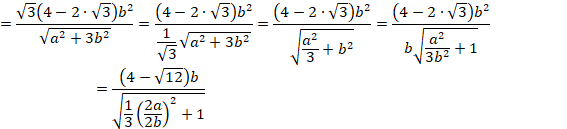
ゆえに、
