�ߘa�R�N�W���Q�Q��
 [���ꐯ]
[���ꐯ]
�@�@��403�����w�I�ȘA�������
�@�@�@�@����W���ԁF7��25���`8��22����
�@�@�@�@�@�@�@�@�m�c��_�Ђ̎Z�z(1)�n

���{�V�S�{�V�����c�@�@�c��_��
�@
�@�@�@�@�@�@��������Z�z�i�{�V���w�蕶�����j�@�@�c�U�T�����`���X�X����
��̎ʐ^�́A�V�ۂP�Q�N�i�P�W�S�P�j�W���Ɋ֗��a�Z�ƒJ���Ζ�l�E�y���M�`��l�������N���Z�z�ł���B
�@����̎O���11����13�܂ł̎����̖��ł��B�����͓����̊�������ǂ��āA�m���߂Ă��������B������㕗�̉œ����Ƃ��܂��B

 �����
�����
�P��
�@���}�̔@�����c����A���m�ς������ān�~�c����Ɨ~���B�����ɉ]���A���ʎ�a��p�@���Ɩ₤�B
�����ĞH���A���ʂ�u���A��@������悶�ē���B
�֗��y���M�`��l�@�\��Γ��@�y���[�g�@�ލl
��Ӂ@�^����ꂽ�����`�ɓ������ʐς����~�̒��a�����߂�B
�Q�l�F�~�������R�D�P�S�Ƃ��Ă��܂��B

�����
�P��
�@���}�̔@�������L��A���Ɏl���̉~��e��āA���ς�݂��B���̍��ώ�A���a��p��₤�@���B
�@�����ĞH���A��ӂ�u���A�����~�ϗ��������A�]���Ȃč��ς���������������J��������ē��a��B
����@�\�O�Γ��@�@����S��Y�@�ލl
�@
�Q�l�@�~�ϗ��Ƃ͉~�̖ʐς����߂�Ƃ��̒萔�B���a�P�̉~�̖ʐς̒萔��/4
��Ӂ@�@�^����ꂽ�����`�̒��Ɏl�̓��~������B���������̖ʐς�m���ē��~�̒��a�����߂�B
��O���
�P��
�@���}�̔@���������ɓ���u�ĂāA�b���O�Ӌy�щ�����ӗL��B�����A�b���ʂ̎���]�āA�����ʂ�p��₤�ɔ@���B
�@�����ĞH���A�܉ӂ�u������������J���A������ӂ������A�]�肱����čb���ʂ��悶�ĉ����ʂ�B
����@�\��Γ��@����약�V��@�ލl
�@
���
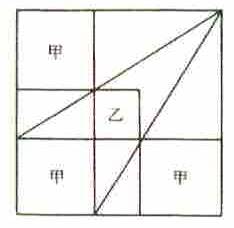
�����`�̓��ɓ�̎ΐ������b�̐����`�O�Ɖ��̐����`�������B�b�̐����`�̈�ӂ̒�����m���ĉ��̐����`�̈�ӂ̒��������߂�B
�@
�Q�l�����@�@�@
�P�@�u���̎Z�z�̉���v�@���؏d���@��
�Q�@�{�V�E��ΒÐ_�Ђ̓��D�E�G�n�E�Õ��������W�@
���_�В��{�V��ΒÎx���@���s�@2018�N���s
�lj����i�ҁ@�W���[�J�[����j�@
�q���g�F���̗��p�B

�u�W���[�J�[�v �@ 7/25 15��56�� ��M �X�V 8/22


�u�W���[�J�[�v �@ 8/20 08��02�� ��M �X�V 8/22
��ꂽ�lj��������ł��B
�܂��A�����ɂ́A�u��x�Ђ����v����̎���́uAG=(���) �Ƃ������ʂ͋����[���ł��D �_G�ɂ́C�Ȃɂ����ʂȖ��̂����Ă���̂ł��傤���H�v
������܂��B
�u��x�Ђ����v
8/12 16��16���@ ��M �X�V 8/22
�lj����̉F
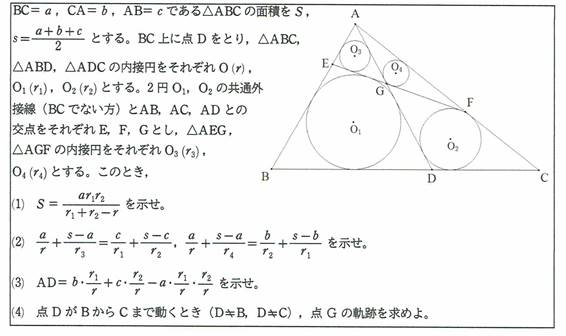
�V���Ɏ���17�̓_���C���}�ɒlj�����D
J_i : ����AB�Ɖ~O_i�Ƃ̐ړ_ (i=1,3)
K_i : ����AD�Ɖ~O_i�Ƃ̐ړ_ (i=1,2,3,4)
L_i : ����AC�Ɖ~O_i�Ƃ̐ړ_ (i=2,4)
M_i : ����BC�Ɖ~O_i�Ƃ̐ړ_ (i=1,2)
N_i : ����EF�Ɖ~O_i�Ƃ̐ړ_ (i=1,2,3,4)
J : ����AB�Ɖ~O�Ƃ̐ړ_
L : ����AC�Ɖ~O�Ƃ̐ړ_
M : ����BC�Ɖ~O�Ƃ̐ړ_
[��1]
��CM_2O_2 �� ��CMO ���C
CM_2=(r_2/r)*CM.
�����ŁC
CM
=(1/2)*(2*CM+2*BJ+2*AL)-(BJ+AL)
=(1/2)*(a+b+c)-(c)
=s-c
�ł��邩��C
CM_2=(r_2/r)*(s-c) --- (0)
DA=BC+CA-BD-2*CM_2 ---(1) �ł���D
�Ȃ��Ȃ�C
DK_2=DM_2=DC-CM_2=BC-BD-CM_2 �����
K_2A=L_2A=CA-CL_2=CA-CM_2�@�Ƃ���C
DA=DK_2+K_2A=BC+CA-BD-2*CM_2.
����āC
(��ABD�̖ʐ�)
=(r_1/2)*(AB+BD+DA)
=(r_1/2)*(AB+BC+CA-2*CM_2)�@(��(1))
=(r_1/2)*(a+b+c-2*CM_2)
=(r_1/2)*(2*s-2*(r_2/r)*(s-c)) (��(0))
=s*(r_1)-(r_1)*(r_2)*(s-c)/r.
�܂��C�Ώ̐��ɂ��C
(��ACD�̖ʐ�)
=s*(r_2)-(r_1)*(r_2)*(s-b)/r.
(��ABC�̖ʐ�)=(��ABD�̖ʐ�)+(��ACD�̖ʐ�)
�ł��邩��C
s*r=s*(r_1)-(r_1)*(r_2)*(s-c)/r + s*(r_2)-(r_1)*(r_2)*(s-b)/r.
����āC
s*(r_1+r_2-r)=(r_1)*(r_2)*(2*s-b-c)/r.
����āC
s*r=a*(r_1)*(r_2)/(r_1+r_2-r) ---(2)
�܂�C
S=a*(r_1)*(r_2)/(r_1+r_2-r)
���������D
[��2]
AJ_1
=AK_1
=AD-DK_1
=AD-DM_1
=AK_2+K_2D-DM_1
=AL_2+DM_2-DM_1
����āC
AB
=AJ_1+J_1B
=(AL_2+DM_2-DM_1)+BM_1 ---(3)
AC
=AL_2+L_2C
=AL_2+M_2C ---(4)
BC=BM_1+M_1D+DM_2+M_2C ---(5)
s-c
=(1/2)*(a+b-c)
=(1/2)*(BC+CA-AB)
=(1/2)*(2*M_1D+2*M_2C) (��(3),(4),(5))
=DM_1+CM_2.
����āC
DM_1
=(s-c)-CM_2
=(s-c)-(r_2/r)*(s-c)
=(s-c)*(1-r_2/r)
�Ώ̐��ɂ��C
DM_2=(s-b)*(1-r_1/r) ---(6)
��O_2M_2D �� ��DM_1O_1 ���C
DM_2
=(r_1)*(r_2)/DM_1
=(r_1)*(r_2)/((s-c)*(1-r_2/r)) ---(7)
(6),(7) ���C
1/((s-c)*(1-r_2/r))=(s-b)*(1-r_1/r)/((r_1)*(r_2)) ---(8)
��AL_4O_4 �� ��AL_2O_2 ���C
AL_4
=((r_4)/(r_2))*AL_2
=((r_4)/(r_2))*(CA-CL_2)
=((r_4)/(r_2))*(CA-CM_2)
=((r_4)/(r_2))*(b-(r_2/r)*(s-c))
=((r_4)/(r_2))*(b)-((r_4)/r)*(s-c) ---(9)
L_4F
=GN_2
=DM_1
=(s-c)*(1-r_2/r) ---(10)
��FL_2O_2 �� ��O_4L_4F ���C
FL_2
=(r_2)*(r_4)/(L_4F)
=(r_2)*(r_4)/((s-c)*(1-r_2/r)) (��(10))
=((r_4)/(r_1))*(s-b)*(1-r_1/r) (��(8)) ---(11)
L_2C=CM_2=(r_2/r)*(s-c) ---(12)
b=AC=AL_4+L_4F+FL_2+L_2C �ł���̂ŁC
����ƁC(9),(10),(11),(12) �Ƃ���C
b=((r_4)/(r_2))*(b)-((r_4)/r)*(s-c)+(s-c)*(1-r_2/r)
+((r_4)/(r_1))*(s-b)*(1-r_1/r)+(r_2/r)*(s-c).
���̓�������C
(a/r)+(s-a)/(r_4)=(b)/(r_2)+(s-b)/(r_1) ---(13)
��D
�܂��C�Ώ̐��ɂ��C
(a/r)+(s-a)/(r_3)=(c)/(r_1)+(s-c)/(r_2)
�ƂȂ�D
[��3]
AD
=AK_2+K_2D
=AL_2+DM_2
=AC-CL_2+DM_2
=AC-CM_2+DM_2
=b-(r_2/r)*(s-c)+(s-b)*(1-r_1/r)
=b*(r_1/r)+c*(r_2/r)-s*((r_1+r_2-r)/r)
=b*(r_1/r)+c*(r_2/r)-(a*(r_1)*(r_2)/(r*(r_1+r_2-r)))*((r_1+r_2-r)/r) (��(2))
=b*(r_1/r)+c*(r_2/r)-a*(r_1)*(r_2)/(r*r).
[��4]
AG=(s-a) �ł��邱�Ƃ������D
K_4G=GN_4=N_2F=FL_2 �ł���̂ŁC
AG
=AK_4+K_4G
=AL_4+FL_2
=((r_4)/(r_2))*(b)-((r_4)/r)*(s-c)+((r_4)/(r_1))*(s-b)*(1-r_1/r) (��(9),(11))
=(r_4)*(b/r_2 + (s-b)/r_1 - a/r)
=(r_4)*((s-a)/(r_4)) (��(13))
=(s-a).
����āC�_G�̋O�Ղ� �_A�𒆐S�Ƃ������a(s-a)�̉~�̗�� JL �ł���D
�������C�[�_ J, L �͏����D
--------------------------------------
AG=(���) �Ƃ������ʂ͋����[���ł��D
�_G�ɂ́C�Ȃɂ����ʂȖ��̂����Ă���̂ł��傤���H
(�ȏ�)
�u��ӂ����̂炢��������v 8/19 20��52���@��M �X�V 8/22
�����
�����`�̈�ӂ�a�A�~�̔��a�����Ƃ��܂��B
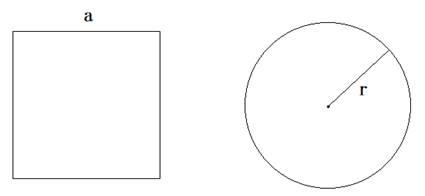
�����`�Ɖ~�̖ʐς��������̂ŁA
![]()
![]()
�����
�~�̔��a�����Ƃ��܂��B
����ƁA�����`�̈�ӂ�4���ł��B

���������̖ʐς����Ƃ���ƁA
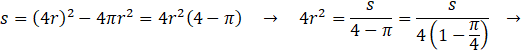

��O���
�����`�b�̈�ӂ�a�A���̈�ӂ����Ƃ��܂��B
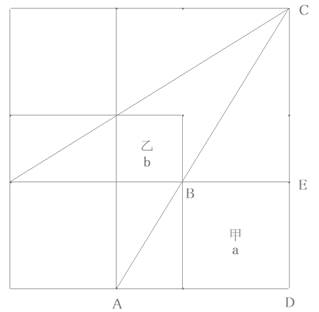
�����`�b�̌X�����A��ʂ�ōl���āA
![]()
����2�������������ɂ��ĉ������̒l�ׂ�ƁA
![]()
�u�X���[�N�}���v
8/19 21��52���@ ��M �X�V 8/22
�W���[�J�[�l�̖��͂����������beyond me �ł�...
�Ƃ肠�����A�ȉ��̖�肾���ł� ^^;v
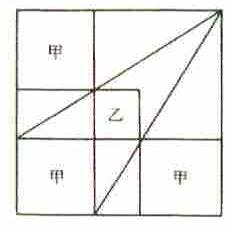 ��O���
��O���
���
�����`�̓��ɓ�̎ΐ������b�̐����`�O�Ɖ��̐����`�������B�b�̐����`�̈�ӂ̒�����m���ĉ��̐����`�̈�ӂ̒��������߂�B
��
�b��1�ӂ̒�����y,����1�ӂ̒�����x�Ƃ����...
���̑����䂩��...
(x+2y)/(x+y)=(x+y)/y
x^2+2xy+y^2=xy+2y^2
x^2+xy=y^2
(x+y/2)^2=5y^2/4=(��5/2)y
so...
�b��1��=x=((��5-1)/2)*y�E�E�E����
������=��=(��5+1)/2 �Ȃ̂�...
x=(��-1)*y
so...
x+y=��*y
x+2y=1 �̂Ƃ�...
y=1/(��+1)=(3-��5)/2=0.3819...
x=1-2/(��+1)=(��-1)/(��+1)=��5-2=0.236...
���̂悤�ȊW�ɂȂ�}���͈�ʂɌ��܂�킯�ł��̂˂� ^^
�}�̒����������邱�Ƃő����E���ʂ����ł��� ^^
