�ߘa�V�N�P�Q���V��
 [���ꐯ]
[���ꐯ]
�@�@��461�����w�I�ȘA�������
�@�@�@����W���ԁF11��11���`12��7����
�m�Q�����n
�@

�lj�����i�o��҂́u�W���[�J�[�v�j�@�V��V���[�Y
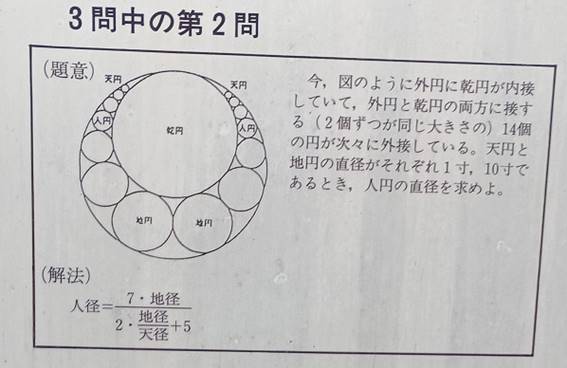
�l���~���̐����`�Ɛ��O�p�`��1�ӂɂ��āw�R�x�@
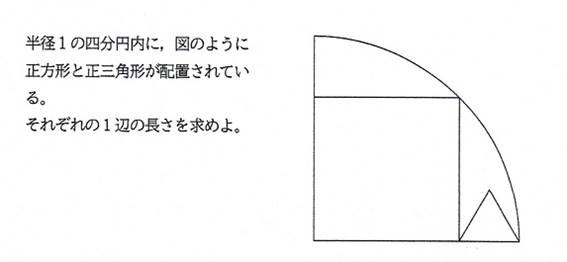
���P�@�@�V���[�Y�P���
�����`�Ɛ��O�p�`��1�ӂ��قȂ�i������),
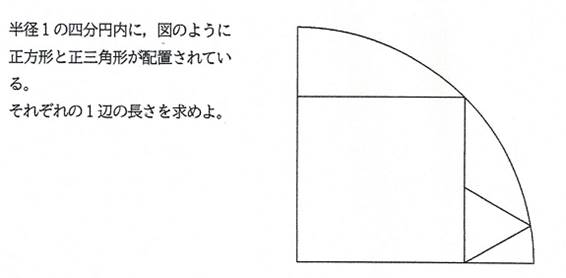
���Q�@�V���[�Y�Q���
�����`�Ɛ��O�p�`��1�ӂ��قȂ�i������),
NO1�u�W���[�J�[�v �@ 11/11�@�@ 20��14�� ��M �X�V 12/7
��ꂽ������
NO2�u�O�p��K�v
11/18
18��09���@ ��M �X�V 12/7
��ꂽ������
NO3�u��ӂ����̂炢��������v 11/26 11��4�� ��M �X�V 12/7
�@��ꂽ������
����̑Q�����̖��́A���ɂ��������ł��B
�i1�j�̕����i2�j�̕������ʂɌv�Z���ĕό`����Ƃ����̂ł͂���܂���B
�i1�j�͓藝�Ɣ�r���Ă����Ȃ�͂����A
�i2�j�͂��̉ŗǂ��̂��Ǝv���܂����A�킩��₷���Ƃ������Ƃł���
���������ӂ��ɍl���܂����B
�Z�z�̖��́A�͂��ߌv�Z����ς��낤�ȁ[�Ƌ���Ă��܂������A���]�@�ł������Ȃ������̂ŁA����قǂł��Ȃ��z�b�Ƃ��܂����B
�u��ӂ����̂炢��������v 11/26 22��26�� ��M �X�V 12/7
�@�@��ꂽ������
���w�E���肪�Ƃ��������܂��B
(2)�ł���1�A2 �̂Ƃ��́Acos ��60���A30�� �̒l�ł��邱�Ƃ́A�킩���Ă��܂������A
�]���̔��p�̒藝�܂ł́A�v�����܂���ł����B
�d��ŁA�]���̋t���̌v�Z������ƁA�p�������ɂȂ��Ă����̂ŁA�Ȃ�قǂƎv���܂����B
���l�������Ă��Ĉ�ʍ���\�z����̂́A�ƂĂ�����ł��B
�q���g���Ȃ��ƂƂĂ������ł��B
NO4�ukasama�v 11/29 16���Q�V���@�@ ��M �X�V 12/�V
��ꂽ������
����̖��ł����A������ЎZ�z�͔��]���g���Ɛ������ꂢ�ɉ����邱�Ƃ�m��܂����B���]�̒m���͂قڊF���ł������A���̍ɂȂ��Ă��A�w�Ԃ��Ƃ������Ɖ��߂Ċ����܂����B
NO5�u��x�Ђ����v 11/30 13��27���@ ��M �X�V 12/7
��461�w�I�ȘA��������̉F
�m�Q�����n
(1)
2^n/n!=��[k=1,n+1]a[k]*a[n+2-k]
---�@
�@�ɂ����āCn=1,2,3�������Ca[1]=1��p���邱�Ƃɂ���āC
a[2]=1, a[3]=1/2, a[4]=1/6
��D����āC
a[n]=1/((n-1)!) ---�A
�Ɨ\�z�ł���D�ȉ��C���̗\�z�����ׂĂ̐�����n�ɑ��Đ�����
���Ƃ�n�Ɋւ���A�[�@�Ŏ����D
n=1,2,3,4�ɑ��ẮC�A�͐������D
r��2�ȏ�̔C�ӂ̐������Ƃ��C1��n��r �Ȃ邷�ׂĂ̐����� n �ɑ��āC
�A���������Ɖ��肷��D
�@����ό`���āC
2*n!*a[n+1]=2^n-n!*��[k=2,n]a[k]*a[n+2-k]
��D
�����n=r�������āC
2*r!*a[r+1]=2^r-r!*��[k=2,r]a[k]*a[r+2-k].
�����ŁC�A�[�@�̉�����C�E�ӂ͎��̂悤�ɕό`�ł���D
2^r-r!*��[k=2,r]a[k]*a[r+2-k]
=2^r-r!*��[k=2,r](1/(k-1)!)*(1/(r+1-k)!)
=2^r-��[k=2,r]binomial(r,k-1)
=2^r-(��[k=1,r+1]binomial(r,k-1)-binomial(r,0)-binomial(r,r))
=2^r-(2^r-2)
=2.
�܂�C2*r!*a[r+1]=2 �ƂȂ�D
���̂��Ƃ��Ca[r+1]=1/(r!)�D
����āCn=(r+1)�̂Ƃ��ɂ��A�͐��������Ƃ��킩��D
�ȏ���C���ׂĂ̐�����n�ɑ��āC�A�͐������D
(2)
(��2)*a[n+1]=��(a[n]+1) ��ό`���āC
a[n+1]=��((a[n]+1)/2) ---�B
�B�ɂ����āCn=1,2 �������Ca[1]=1/2
��p���邱�Ƃɂ���āC
a[2]=(1/2)*��(3),�@a[3]=(1/2)*(��6+��2)
��D����āC
a[n]=cos((2^(1-n))*(��/3))
---�C
�Ɨ\�z�ł���D�ȉ��C���̗\�z�����ׂĂ̐�����n�ɑ��Đ�����
���Ƃ�n�Ɋւ���A�[�@�Ŏ����D
n=1,2,3�ɑ��ẮC�C�͐������D
r��2�ȏ�̔C�ӂ̐������Ƃ��Cn=r�̂Ƃ��C�C���������Ɖ��肷��D
���̂Ƃ��C�B���C
a[r+1]
=��((a[r]+1)/2)
=��((cos((2^(1-r))*(��/3))+1)/2)
=��((cos(2^(-r)*(��/3)))^2) ( �����p�̌���
(cos(��/2))^2 = (1/2)*(cos(��)+1) ) =(cos(2^(-r)*(��/3)).
����āCn=r+1�̂Ƃ��ɂ� �C�͐��������Ƃ��킩��D
�ȏ���C���ׂĂ̐�����n�ɑ��āC�C�͐������D
[����א_�ЎZ�z]
�l�~�̒��a�́C14/5(��) =
2.8(��) = 2��8�� (��)
�O�~�̒��a��1/r�C���~�̒��a��1/R �Ƃ���D(0<r<R)
�O�~�Ɗ��~�̗����ɐڂ���14�̉~�̂����C���}�̉E�����ɂ���7�̉~���C
���̔��a�̑傫�����ɁC��[1],��[2],�c,��[7]�Ƃ���D
�܂��C�~��[k]�̒��a�� s[k] �Ƃ���D(k=1,2,�c,7)
�O�~�Ɗ��~�Ƃ̐ړ_�����_O�Ƃ��C���~�̒��S�̍��W��
(1/(2*R),0)�ƂȂ�悤��xy�������W��ݒ肵�čl����D
���_O�𒆐S�Ƃ��锼�a 1 �̉~�Ɋւ��锽�]�� I �Ƃ���D
���]I�ɂ���āC�O�~�͒��� x=r�ɁC���~�͒��� x=R �Ɉڂ�D
�܂��C�~��[1],��[2],�c,��[7]�́C�}�̂悤�ȁC
���ׂĒ��a�̓������~��[1],��[2],�c,��[7]�Ɉڂ�D
( �}�� https://fpseries.exblog.jp/33836778/ )
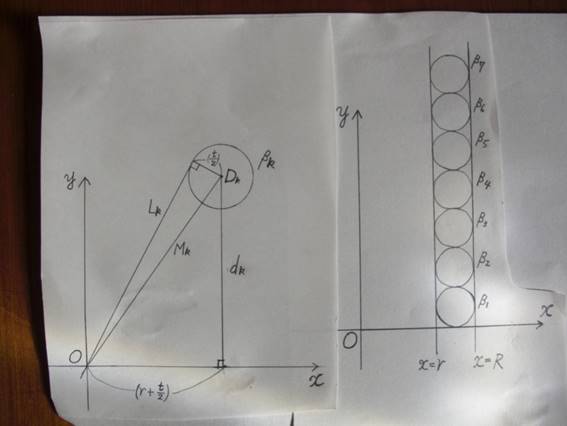
�~��[k]�̒��a�� t�C��[k]�̒��S��D[k]�Ƃ��Cd[k],M[k],L[k]��}�̂悤��
�����̒����Ƃ���D���̂Ƃ��C����4�������藧���Ă���D
d[k]=(k-1/2)*t,
(M[k])^2=(r+t/2)^2+(d[k])^2,
(M[k])^2=(L[k])^2+(t/2)^2,
(L[k])^2=t/s[k].
�����4�����C
(r+t/2)^2+((k-1/2)*t)^2 =
t/s[k]+(t/2)^2 ---(��)
(��)�ɂ����āCk=1�������āC
(r+t/2)^2 = t/s[1].
(��)�ɂ����āCk=7�������āC
(r+t/2)^2 = t/s[7]-42*t^2.
����āCt=(1/42)*(1/s[7]-1/s[1]).
s[k]�� k,s[1],s[7] ��p���ĕ\���Ǝ��̂悤�ɂȂ�D
s[k]
=t/(L[k])^2
=t/((M[k])^2-(t/2)^2)
=t/((r+t/2)^2+((k-1/2)*t)^2-(t/2)^2)
=t/(t/s[1] + k*(k-1)*t^2 )
=s[1]/(1+s[1]*k*(k-1)*t)
=s[1]/(1+s[1]*k*(k-1)*(1/42)*(1/s[7]-1/s[1]))
=42*s[1]/(
k*(k-1)*s[1]/s[7] + 42-k*(k-1) ).
�����k=4�������āC
s[4]
=42*s[1]/(12*s[1]/s[7]+30)
=7*s[1]/(2*s[1]/s[7]+5).
�{��́Cs[1]=(10��),
s[7]=(1��) �̏ꍇ�ł��邩��C
s[4]=7*10/(2*10+5)=14/5 (��)
(���]�@���g�����ƂȂ��C�a�Z�Ƃ����͂��̖���
���������ǂ̂悤�ɉ����Ă����̂ł��傤���B
�ނ�̐��܂����܂ł̏�M�C���O�������܂��D)
(�ȏ�)
�u���̗���v �@�@�@�@�@�@�@�@�@�@�@�@�@�@
�X�V 12/�V


����א_�ЎZ�z���̓��@���Ŕ�����������

 �F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���, �ƃy���l�[����Y����, ���[���ő����Ă��������B�҂��Ă��܂��B
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���, �ƃy���l�[����Y����, ���[���ő����Ă��������B�҂��Ă��܂��B
