暯惉侾俈擭侾侽寧俀俁擔
 [棳傟惎]
[棳傟惎]
丂丂丂丂丂戞161夞悢妛揑側墳曞栤戣夝摎NO1
丂丂丂丂丂丂亙夝摎曞廤婜娫丗俋寧俀俆擔乣侾侽寧俀俁擔
乵曮偝偑偟乶
奆偝傫丄崱夞偺墳曞婜娫偼侾儢寧偲偟傑偡丅偙偙偱栤戣偱偡丅
丂俙俛亖俙俠偺擇摍曈嶰妏宍俙俛俠偺搚抧偑偁傝傑偡丅懢榊偝傫偼俙俹亄俛俹亄俠俹偺挿偝偑嵟彫偵側傞揰俹偵曮暔傪杽傔傑偟偨丅
曮暔偑杽傑偭偰偄傞揰俹偑偳偙偐峫偊偰偔偩偝偄丅偨偩偟丄捀妏佢俛俙俠偼侾俀侽亱埲撪偲偟傑偡丅
NO1乽uchinyan乿9/25丂17帪07暘庴怣 峏怴10/23
戞161夞悢妛揑側墳曞栤戣傊偺夝摎
仮ABC 偵懳偟偰丄佢APB = 佢BPC = 佢CPA = 120搙丄偲側傞揰 P 偑摎偊丅
徹柧偼丄椺偊偽丄仮APB 傪 B 傪拞怱偵60搙夞揮偟偰丄
A, P 偺堏摦愭傪 D, Q 偲偟傑偡丅
仮DAB 偼惓嶰妏宍偱丄D 偼丄仮ABC 偑寛掕偡傟偽寛掕偡傞屌掕偝傟偨揰偱偡丅
傑偨丄佢ABC < 120搙側偺偱丄D 偼丄BC 媦傃偦偺墑挿偵娭偟偰丄
A 偲摨偠懁偵偁傝傑偡丅
夞揮偺惈幙偐傜丄仮APB 佭 仮DQB 側偺偱丄AP = DQ丄
仮BPQ 偼惓嶰妏宍傛傝丄BP = BQ = QP丅
偮傑傝丄AP + BP + CP = DQ + QP + PC 偲側傝丄
D 偲 C 偲傪寢傇捈慄偑嵟彫偱偡丅
媡偵嵟彫偺偲偒丄揰 Q, P 傪 DC 忋偵丄仮APB 佭 仮DQB 偲側傞傛偆偵偲傟偽丄
佢DBA = 60搙側偺偱丄仮BPQ 偑惓嶰妏宍偵側傝丄佢APB = 佢DQB = 120搙丄
佢BPC = 120搙丅
偦偙偱丄偝傜偵丄佢CPA = 120搙丅
(姶憐)
戞161夞悢妛揑側墳曞栤戣偱偡偑丄僔儏僞僀僫乕揰枖偼僼僃儖儅乕揰丄偲偄偆傕偺偱偡偹丅
埲慜偵夝偄偨偙偲偑偁偭偨偺偱丄傂偲傑偡丄偦偺夝摎傪憲傝傑偟偨丅
NO2乽H7K乿
9/25丂22帪46暘庴怣 峏怴10/23
乽AP+BP+CP嵟彫乿偐傜丆懄嵗偵Fermat揰傪巚偄弌偟傑偟偨丏
偑丆娞怱偺偦偺撪梕偼朰傟偰偟傑偄丆巚偄弌偡偺偵偐側傝帪娫偑偐偐傝傑偟偨丏
堦斒偺応崌傪愭偵峫偊傑偡丏
A傪拞怱偵丆C, P傪60亱夞揮偝偣丆偦傟傪C', P'偲偟傑偡丏
偙偺偲偒丆P偺庢傝曽傛傝丆AP=AP'丆佢PAP'=60亱傛傝丆AP=PP'丏
堦曽丆夞揮側偺偩偐傜丆摉慠CP=C'P'丏傛偭偰丆PA+PB+PC=BP+PP'+P'C>=BC'丏
傛偭偰丆偙偺幃偺摍崋偑惉傝棫偮傛偆側丆懄偪佢APB=佢BPC=佢CPA=120亱
偱偁傞傛偆側P偑偁傟偽丆偦傟偑媮傔傞揰偲側傞丏
佢A, 佢B, 佢C<120亱偺偲偒傪傑偢峫偊傞丏
偙偺偲偒丆忋偵彂偄偨忦審傪枮偨偡P偼懚嵼偟丆埲壓偺庢傝曽偱嶌恾偱偒傞丗
AB, BC, CA傪堦曈偲偡傞惓嶰妏宍ABC', BCA', CAB'傪丆尦偺嶰妏宍偺奜懁偵偦傟偧傟嶌傞丏
偡傞偲丆AA', BB', CC'偼堦揰偱岎傢傝丆偙傟偑媮傔傞揰丏
(徹柧偼側傫偩偐偛偭偪傖偵側偭偰偟傑偭偨偺偱屻偱乯
堦曽丆偳傟偐1偮偺妏偑120亱傛傝戝偒偄応崌丆偦偺妏偑佢A偱偁傞偲偡傞偲丆
乽AP+BP+CP嵟彫乿偺揰偼P=A偱偁傞丏偙偺偲偒丆榓偼AB+AC偲側傞丏
[徹柧]
1. PB+PC=AB+AC偺揰偺廤崌偼懭墌偲側傞丏懭墌奜晹偱偼丆PA+PB+PC>PB+PC>AB+AC丏
2. 懭墌忋偱偼丆P=A偱側偄側傜丆PA>0傛傝丆PA+PB+PC>PB+PC=AB+AC丏
3. 嶰妏宍偺廃忋丏P伕BC偱側偄偲偒偼丆嶰妏宍偺宍忬偐傜丆P=A偑嵟抁丏
乮P伕BC偺偲偒偼丆屻偺7.偱峫偊傞丏乯
4. 懭墌撪偺壓敿暘偵偮偄偰偼丆摉慠忋敿暘偺懳墳偡傞揰偵斾傋PA偑挿偄偼偢丏
5. 懭墌偲AB偱埻傑傟傞椞堟撪偺応崌丏傑偢丆柧傜偐偵PA+PB>AB丏傑偨丆嶰妏宍偺
宍忬偐傜丆偙偺椞堟偲丆QA<=AC偺廤崌乮暵墌斅乯偲偼嫟捠晹暘偑側偄丏
乮墌廃偺A偵偍偗傞愙慄傪堷偄偰峫偊傟偽椙偄乯傛偭偰PC>AC丏
6. 懭墌偲AC偱埻傑傟傞椞堟撪偺応崌丏5.偲慡偔摨條丏
7. 嶰妏宍偺撪晹丆傕偟偔偼BC忋丏
佢A, 佢B, 佢C<120亱偺偲偒偲摨條偵嶌恾偟偰傒傞丏偟偐偟丆P偺埵抲偺惂尷偐傜丆
B--P--P'--C'偼丆敿捈慄AB, AC'偵傛傝嬫愗傜傟傞敿暯柺偺偆偪C偑偁傞曽丆偺忋傪
捠偭偰偄傞偙偲偲側傞丏偙偺偨傔丆偳偆偁偑偄偰傕丆P=A偺偲偒傛傝抁偔偡傞偙偲偼偱偒側偄丏
埲忋傛傝丆媮傔傞揰偼丆P=A丏//
偙偺栤戣偺応崌丆柧傜偐偵佢A, 佢B, 佢C<120亱偺偲偒偱偁傞丏擇摍曈嶰妏宍偺懳徧惈傕巊偆偲丆
傑偢A偐傜BC偵岦偐偭偰悅慄傪堷偒丆師偵仮ABC偺奜懁偵惓嶰妏宍CB'A傪嶌傞丏
AB'偲悅慄偺岎揰偑媮傔傞P偱偁傞
乽H7K乿
9/26丂21帪39暘庴怣 峏怴10/23


NO3乽僪儞僉乕乿9/26 21帪52暘庴怣 峏怴10/23
乽夝摎乿
傑偢丄戣堄傪枮偨偡揰俹偼慄暘俛俠偺悅捈擇摍暘慄忋偵偁傞偙偲傪帵偟傑偟傚偆丅
仮俙俛俠偺撪晹偵偁傝丄慄暘俛俠偺悅捈擇摍暘慄忋偵偁傞掕揰俻偵懳偟偰丄揰俛丄俠傪徟揰偲偟丄揰俻傪捠傞傛偆側懭墌傪偲傝傑偡丅
偦偺懭墌忋偱揰俹傪摦偐偡偲偒丂BP+CP=BQ+CQ=堦掕丂偱偡偹丅
偦偟偰柧傜偐偵AP亞AQ偱偡丅
傛偭偰丂AP+BP+CP亞AQ+BQ+CQ丂偑惉傝棫偪傑偡丅
摍崋惉棫偼揰俹偲揰俻偑堦抳偡傞偲偒偱偡丅
偙傟偼丄揰俻偑慄暘俛俠偺悅捈擇摍暘慄忋偵偁傟偽丄偳偆摦偐偟偰傕忢偵惉傝棫偪傑偡偹丅
偙傟偱戣堄傪枮偨偡揰俹偼慄暘俛俠偺悅捈擇摍暘慄忋偵偁傞偙偲偑暘偐傝傑偟偨丅
偙偙傑偱棃傟偽傕偆堦懅偱偡丅
慄暘俛俠偺拞揰傪俵偲偟丄慄暘俙俵忋偵揰俹傪偲傝傑偡丅
傑偨PM=p偲偍偔偲丄揰俹偼仮ABC偺撪晹偵偁傝傑偡偐傜丂0亙倫亙AM丂丒丒丒嘆丂偱偡丅
偙偙偱丄捀妏偑120亱埲壓偱偁傞偲偄偆忦審偐傜佢ABM亞30亱偩偲暘偐傝傑偡丅
傛偭偰丄AM亞BM倲倎値30亱=BM/sqrt(3)丂丒丒丒嘇丂偱偡丅
偙偺偲偒丂BP+CP=2BP=2sqrt(PM^2+BM^2)=2sqrt(p^2+BM^2)丂偱偡偐傜
AP+BP+CP=AM-p+2sqrt(p^2+BM^2)
偙偺椉曈傪倫偱旝暘偡傞偲
倓乮AP+BP+CP乯/dp=-1+2p/sqrt(p^2+BM^2)
丒丒丒乮仏乯
偙偙偱丂乮仏乯=0丂丂佁丂丂p^2+BM^2=4p^2
佁丂丂p=BM/sqrt(3)
傑偨丄偙偺慜屻偱乮仏乯偼晧偐傜惓偵曄傢傝傑偡丅
傛偭偰AP+BP+CP偼丄p=BM/sqrt(3)丂偺偲偒嬌彫偐偮嵟彫偵側傝傑偡丅
嘆嘇傛傝丄偙偺偲偒揰俹偼偟偭偐傝仮ABC偺撪晹偵偁傝傑偡丅
埲忋傛傝丄曮暔偑杽傑偭偰偄傞偺偼慄暘俛俠偺悅捈擇摍暘慄忋偱丄佢PBC=30亱偺傪枮偨偡揰俹偺埵抲偵偁傝傑偡丅
乮姶憐乯恾側偄偺偱暘偐傝偵偔偄偐傕偟傟傑偣傫偑丄偛姩曎傪丅
丂丂丂丂偦傟偵偟偰傕丄偳偆傕偙偺夝偒曽偱偼柺敀偔側偄偱偡偹丅
丂丂丂丂傕偭偲婔壗揑偵夝偗傞偲巚偆傫偱偡偗偳丄偦傟偼懠偺曽乆偺夝摎傪妝偟傒偵偟偰偍偒傑偡丅
乽僪儞僉乕乿9/27 14帪05暘庴怣 峏怴10/23
崱擭僷僜僐儞傪攦偭偨傫偱偡偗偳丄偄傠偄傠僱僢僩傪偝傑傛偭偰偄傞偲乽Weekend Mathmatics乿偵偨偳傝拝偒傑偟偨丅偦偙偱偙偺栤戣偺偙偲傪抦傝丄憲傜偣偰傕傜偄傑偟偨丅
悢妛偼岲偒偱偡丅抦傜側偄偙偲偑偨偔偝傫偁傝丄偦偺墱偺怺偝偵儚僋儚僋偟傑偡丅傑偨乮暘偐傟偽偺榖偱偡偑乯丄偙傟偐傜傕夝摎傪憲傝偨偄偲巚偄傑偡丅
堦斒偺嶰妏宍偵偮偄偰傕峫偊偰偔偩偝偄偲偄偆偙偲偱偟偨偺偱丄峫偊偰傒傑偟偨丅
傑偢偼丄擇摍曈嶰妏宍偵偮偄偰偼傕偆摎偑弌偰偄傞偺偱丄偦傟傪懌偑偐傝偵偟偨偄偲巚偄傑偡丅
杔偼摎偵乽慄暘BC偺惒捈擇摍暘慄忋偵偁傝丄佢PBC=30亱偱偁傞揰俹乿偲昤偒傑偟偨偑丄
偙傟偱偼偁傑傝偵擇摍曈嶰妏宍偵棅傝偡偓偨摎偱丄堦斒壔偱偒偦偆偵偁傝傑偣傫丅
偟偐偟偙傟傪乽佢APB=佢BPC=佢CPA=120亱乿偲撉傒懼偊傟偽丄妶楬偑尒弌偣傑偡丅
崱傑偱偺宱尡忋丄恾宍偵娭偡傞嵟戝嵟彫偺栤戣偼偙偆偟偨偒傟偄側忦審偺偲偒偵幚尰偟偨偐傜偱偡丅
偙傟偑摎偱偼丠偲捈姶偟傑偡丅
偟偐偟偙傟偱偼壗偺徹柧偵傕側偭偰偄傑偣傫丅偙偙偐傜偑杮斣丅
120亱偲偄偆妏搙偼丄180亱亅60亱偱偡丅
60亱偲偄偊偽惓嶰妏宍偑晜偐傃傑偡丅
偆傑偔惓嶰妏宍傪嶌傟側偄偩傠偆偐丠偲峫偊傑偡丅
曈俛俠偵娭偟偰揰俙偲斀懳懁偵丄仮俠俛俛乫偑惓嶰妏宍偵側傞傛偆側揰俛乫傪偲傝丄
摨偠懁偵丄仮俠俹俹乫偑惓嶰妏宍偲側傞傛偆側揰俹乫傪偲傝傑偡丅
偡傞偲丄仮俠俹俛偲仮俠俹乫俛乫偑崌摨偵側傝傑偡偹丅乮擇曈偲嫴妏乯
傛偭偰丂丂俙俹+俛俹+俠俹亖俙俹+俛乫俹乫+俹俹乫丂偵側傝傑偡丅
愜傟慄俙俹俹乫俛偺挿偝偼丄偦傟偑捈慄偵側偭偨偲偒嵟彫偵側傞偺偱丄
俙俹+俛俹+俠俹亖俙俹+俹俹乫+俹乫俛乫亞俙俛乫
摍崋偼係揰俙丆俹丆俹乫丆俛乫偑堦捈慄忋偵偁傞偲偒丄
偡側傢偪丂佢俠俹俙亖180亱亅佢俠俹俹乫亖180亱亅60亱亖120亱丂偐偮丂佢俛俹俠亖佢俛乫俹乫俠亖180亱亅佢俠俹乫俹亖180亱-60亱亖120亱丂
偺偲偒偱偡丅偙傟偱嵟弶偺捈姶偑惓偟偐偭偨偙偲偑帵偝傟傑偟偨丅
崱夞傕恾偑偁傝傑偣傫丅昤偒曽偑暘偐傜側偄傫偱偡丅曌嫮偟傑偡丒丒丒
乮姶憐乯
嵟弶偵161傪夝偄偨偲偒偐傜丄擇摍曈嶰妏宍偠傖側偔偰傕揰俹偼媮傑傞傫偩傠偆側乣偲偼巚偭偨傫偱偡偑丄
偄偄曽朄偑晜偐偽偢偵嵗昗偱夝偒丄偦偺寢壥擇摍曈嶰妏宍偲偄偆恾宍偺惈幙傪僼儖偵妶梡偟偰夝摎偡傞偙偲偵側傝傑偟偨丅
偨偩偦傟偼柍懯偱偼側偔丄摎傪愭偵抦傞偒偭偐偗偵側偭偰偔傟傑偟偨丅
堦斒壔傪峫偊傞偲偒偵摿庩側椺傪懌偑偐傝偵偡傞偲偄偺偼傛偔偁傞偙偲偱丄崱夞傕偦偺椺偱偡偹丅
忋偺夝摎傪峫偊傞偺偼丄寢壥傪偁傞掱搙尒捠偟偰側偄偲擄偟偄偱偡偐傜丅
杔偼偙偺庤偺恾宍栤戣偼嬯庤側偺偱丄側偍偝傜161傪峫偊偨偙偲偑戝偒偐偭偨偱偡丅
偲偙傠偱丄偙傟傪巐柺懱偵奼挘偡傞偲偳偆側傞傫偱偟傚偆偐丠
偮傑傝丄巐柺懱俙俛俠俢偺撪晹偵揰俹傪偲傞偲偒丄俙俹+俛俹+俠俹+俢俹偑嵟彫偵側傞傛偆側揰俹偼偳傫側応強偐丄偲偄偆栤戣偱偡丅
惓巐柺懱偺偲偒偼丄偍偦傜偔廳怱偑偦偺揰偵偁偨傞偱偟傚偆偐傜丄寁嶼偟偰尒傞偲揰俹偼
佢俙俹俛亖佢俛俹俠亖佢俠俹俢亖佢俢俹俙亖兤丂丂偨偩偟丂cos兤亖-1/3
傪枮偨偡揰偩偲偄偆偙偲偑傢偐傝傑偡丅
偙傟偑堦斒偺応崌偵惉傝棫偮丄偲婜懸偟傑偡偑丄杔偵偼偪傚偭偲帵偣偦偆偵偁傝傑偣傫丅
傑偨偳側偨偐偑峫偊偰偔傟偰偄傞偙偲傪婩傝傑偡丅
162傕妝偟傒偵偟偰偄傑偡丅
NO4乽kashiwagi乿9/28
7帪28暘庴怣 峏怴10/23
乽kashiwagi乿9/28 20帪26暘庴怣 峏怴10/23
丂崱丄擇摍曈嶰妏宍ABC偺撪晹偵揰P傪偲傞丅偙偺揰傪捠傞捈慄BC偵暯峴偡傞慄DE傪堷偔丅偦偙偱慄暘BP偲慄暘CP偺榓偼揰C偺慄DE偵懳偡傞懳徧揰C乪偲B傪寢傇捈慄偲側傞丅偲偙傠偱丄偙偺捈慄BC乫偼擇摍曈嶰妏宍偺惈幙偐傜捈慄DE偺拞揰O傪捠傞丅枖丄慄暘AP偺嵟彫抣偼捈慄偱偁傞偺偱AO偲側傞丅懄偪揰P偑揰O偲側傞帪AP亄BP亄CP偺挿偝偼嵟彫偲側傞丅
丂偦偙偱丄揰P傪悅捈擇摍暘慄忋偵偲傝丄掙曈偺挿偝傪2a偲偟掙曈傪倶幉丄悅捈擇摍暘慄傪倷幉偵偲傞丅揰P偺嵗昗偼乮0丄倷乯揰B偲C偼奺乆乮-a丄0乯乮a丄0乯偱偁傞偐傜丄AP亄BP亄CP偺挿偝傪F乮倷乯偲偡傞偲丄
丂丂F乮倷乯亖倐-倷亄2併a2亄倷2丂偲側傞丅偦偙偱偙偺幃傪旝暘偟丄僛儘偲偍偄偰倷傪媮傔傞丅
F乪乮倷乯亖-1亄2倷/併a2亄倷2丂亖0丂傛傝丄倷亖a/併3偱嬌彫抣傪偲傞丅偙偺応崌偙偺抣偑嵟彫抣偱傕偁傞丅
偲偙傠偱丄捀妏偼嵟戝偱傕120亱偱偁傞偺偱丂a/倐丂亝併3偱偁傞丅懄偪a/併3亝倐偲側傝
昁偢嶰妏宍偺撪晹偐捀揰忋偵揰P偑偁傞偙偲偑暘偐傞丅場偭偰偙偺P揰偼戣堄傪枮偨偡丅
丂場偭偰丄媮傔傞揰P偼悅捈擇摍暘慄忋偺捀揰A偐傜丂2倐/併3偺強偲側傞丅
NO5乽昹揷柧枻乿9/29 11帪17暘庴怣 峏怴10/23
恾宍偺栤戣側偺偱丆Visual Basic偱夝偄偨丏
揰俛丆俠傪屌掕偟丆俛(亅侾丆侽)丆俠(侾丆侽)偲偡傞丏佢俛俙俠亝侾俀侽亱偱偁傞偐傜丆俙(侽丆俙倶)乮俙倶亞侾乛併俁乯偲偡傞丏
丂俙俛亖俙俠偱偁傞偐傜丆懳徧惈傪峫椂偟丆揰俹偼佢俛俙俠偺擇摍暘慄忋丆偁傞偄偼偦偺捈慄偵傛偭偰暘偗傜傟傞椞堟偺揰俛偺懚嵼偡傞曽偵偁傞偲偟偰傕丆堦斒惈偼幐傢傟側偄丏
丂栤戣暥偐傜丆揰俹偼搚抧仮俙俛俠偺廃傑偨偼撪晹偵偁傞偲偼尷傜傟偰偄側偄偺偱丆
丂丂俹(俹倶丆俹倷)丆亅侾.俆亝俹倶亝侽丆亅侽.俆亝俹倷亝俀.俆
偲偟偰丆僔儔儈偮傇偟偱俙俹亄俛俹亄俠俹偑嵟彫偲側傞揰傪尒偮偗偰偄偔丏
丂偙偺僾儘僌儔儉偵傛傝丆揰俹偼佢俛俙俠偺擇摍暘慄忋偵偁傝丆佢俛俹俠亖侾俀侽亱偲側傞帠偑暘偐傞丏
丂偪側傒偵丆偙偺僾儘僌儔儉偱偼丆佢俛俙俠亜侾俀侽亱偲側傞応崌傕媮傔傞傛偆偵偟偰偁傞丏偙偺応崌偼揰俹偼揰俙偲堦抳偡傞丏
乮僾儘僌儔儉乯
Option Explicit
Sub Form_Load()
丂丂Picture1.Scale (-1.5, 2.5)-(1.5, -0.5)
丂丂Picture1.BackColor = vbWhite
丂丂Picture3.BackColor = vbWhite
End Sub
Sub Command1_Click()
丂丂Call sakuzu(1)
End Sub
Sub Command3_Click()
丂丂Call sakuzu(2)
End Sub
Sub sakuzu(ByVal n As
Integer)
丂丂Dim Ax As Double
丂丂Dim Ay As Double
丂丂Dim Bx As Double
丂丂Dim By As Double
丂丂Dim Cx As Double
丂丂Dim Cy As Double
丂丂Dim Px As Double
丂丂Dim Py As Double
丂丂Dim Px_min As Double
丂丂Dim Px_max As Double
丂丂Dim Py_min As Double
丂丂Dim Py_max As Double
丂丂Dim Px_min0 As Double
丂丂Dim Px_max0 As Double
丂丂Dim Py_min0 As Double
丂丂Dim Py_max0 As Double
丂丂Dim Pxx As Double
丂丂Dim Pyy As Double
丂丂Dim AP As Double
丂丂Dim BP As Double
丂丂Dim CP As Double
丂丂Dim kizami As Double
丂丂Dim wa As Double
丂丂Dim min As Double
丂丂Dim dankai As Integer
丂丂Dim dankai_max As Integer
丂丂Randomize Timer
丂丂Ax = 0
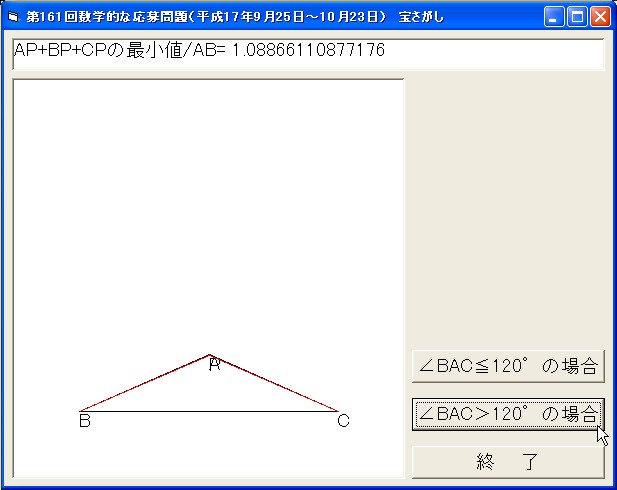
丂丂If n = 1 Then
丂丂丂Ay = Rnd * (2.5 - 1 / Sqr(3))
+ 1 / Sqr(3) '佢BAC=120亱<--> Ay=1/sqr(3)
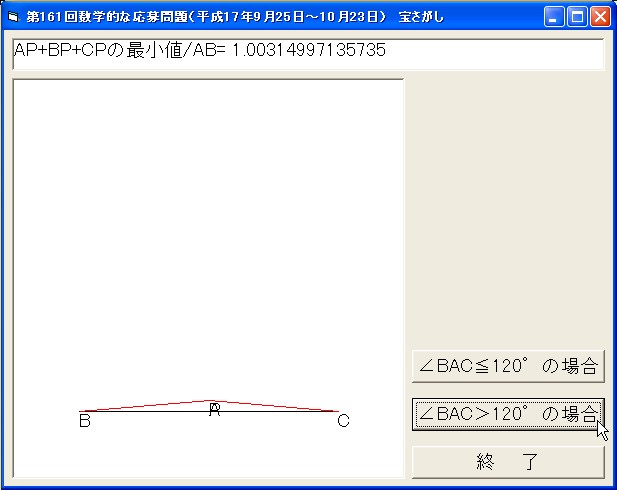
丂丂Else
丂丂丂Ay = Rnd * 1 / Sqr(3)
丂丂End If
丂丂Bx = -1
丂丂By = 0
丂丂Cx = 1
丂丂Cy = 0
丂丂Px_min0 = -1.5
丂丂Px_max0 = 0
丂丂Py_min0 = -0.5
丂丂Py_max0 = 2.5
丂丂kizami = 0.02
丂丂min = 1000000
丂丂dankai_max = 14
丂丂For dankai = 1 To dankai_max
+ 1
丂丂丂If dankai = 1 Then
丂丂丂丂Px_min = Px_min0
丂丂丂丂Px_max = Px_max0
丂丂丂丂Py_min = Py_min0
丂丂丂丂Py_max = Py_max0
丂丂丂ElseIf dankai <= dankai_max Then
丂丂丂丂Px_min = max2(Pxx - kizami, Px_min0)
丂丂丂丂Px_max = min2(Pxx + kizami, Px_max0)
丂丂丂丂Py_min = max2(Pyy - kizami, Py_min0)
丂丂丂丂Py_max = min2(Pyy + kizami, Py_max0)
丂丂丂丂kizami = kizami * 0.1
丂丂丂Else
丂丂丂丂Px_min = Pxx
丂丂丂丂Px_max = Pxx
丂丂丂丂Py_min = Pyy
丂丂丂丂Py_max = Pyy
丂丂丂End If
丂丂丂For Px = Px_min To Px_max Step kizami
丂丂丂丂For Py = Py_min To Py_max Step kizami
丂丂丂丂丂If dankai <= dankai_max
Then
丂丂丂丂丂丂AP = Sqr((Px - Ax) *
(Px - Ax) + (Py - Ay) * (Py - Ay))
丂丂丂丂丂丂BP = Sqr((Px - Bx) * (Px - Bx)
+ (Py - By) * (Py - By))
丂丂丂丂丂丂CP = Sqr((Px - Cx) * (Px - Cx)
+ (Py - Cy) * (Py - Cy))
丂丂丂丂丂丂wa = AP + BP + CP
丂丂丂丂丂丂If min > wa Then
丂丂丂丂丂丂丂min = wa
丂丂丂丂丂丂丂Pxx = Px
丂丂丂丂丂丂丂Pyy = Py
丂丂丂丂丂丂丂Picture3.Cls
丂丂丂丂丂丂丂Picture3.Print "AP+BP+CP偺嵟彫抣/AB="; min / (Cx
- Bx)
丂丂丂丂丂丂End If
丂丂丂丂丂丂Picture1.Cls
丂丂丂丂丂丂Picture1.Line (Ax, Ay)-(Pxx, Pyy), vbGreen
丂丂丂丂丂丂Picture1.Line -(Bx, By), vbGreen
丂丂丂丂丂丂Picture1.Line (Cx, Cy)-(Pxx,
Pyy), vbGreen
丂丂丂丂丂Else
丂丂丂丂丂丂Px = Pxx
丂丂丂丂丂丂Py = Pyy
丂丂丂丂丂丂Picture1.Cls
丂丂丂丂丂End If
丂丂丂丂丂Picture1.Line (Ax, Ay)-(Bx, By), vbBlack
丂丂丂丂丂Picture1.Line -(Cx, Cy), vbBlack
丂丂丂丂丂Picture1.Line -(Ax, Ay), vbBlack
丂丂丂丂丂Picture1.Line -(Px, Py),
vbBlack
丂丂丂丂丂Picture1.Line -(Bx, By), vbBlack
丂丂丂丂丂Picture1.Line (Cx, Cy)-(Px,
Py), vbBlack
丂丂丂丂丂Picture1.CurrentX = Ax
丂丂丂丂丂Picture1.CurrentY = Ay
丂丂丂丂丂Picture1.Print "A"
丂丂丂丂丂Picture1.CurrentX = Bx
丂丂丂丂丂Picture1.CurrentY = By
丂丂丂丂丂Picture1.Print "B"
丂丂丂丂丂Picture1.CurrentX = Cx
丂丂丂丂丂Picture1.CurrentY = Cy
丂丂丂丂丂Picture1.Print "C"
丂丂丂丂丂Picture1.CurrentX = Px
丂丂丂丂丂Picture1.CurrentY = Py
丂丂丂丂丂Picture1.Print "P"
丂丂丂丂Next Py
丂丂丂Next Px
丂丂Next dankai
丂丂'
丂丂If n = 1 Then
丂丂丂Px = Ax
丂丂丂Py = 1 / Sqr(3)
丂丂丂Picture3.Cls
丂丂丂Picture3.Print "佢BPC=120亱"
丂丂End If
丂丂Picture1.Line (Ax, Ay)-(Px, Py),
vbRed
丂丂Picture1.Line -(Bx, By), vbRed
丂丂Picture1.Line (Cx, Cy)-(Px,
Py), vbRed
End Sub
Sub Command2_Click()
丂丂Unload Me
End Sub
Private Function min2(ByVal x As Double, ByVal y As Double) As Double
丂丂If x < y Then
丂丂丂min2 = x
丂丂Else
丂丂丂min2 = y
丂丂End If
End Function
Private Function max2(ByVal x As Double, ByVal y As Double) As Double
丂丂If x > y Then
丂丂丂max2 = x
丂丂Else
丂丂丂max2 = y
丂丂End If
End Function
NO6乽cbc乿丂丂 9/30 00帪17暘庴怣 峏怴10/23
亙僐儊儞僩丗崱夞偼擇摍曈嶰妏宍偱梕堈偩偭偨偺偱偡偑丄堦斒偺嶰妏宍偱偼偳偺傛偆偵側傞偺偱偟傚偆偹丅亜
丂
No7乽偺偭偙傫乿10/01 15帪54暘庴怣 峏怴10/23
曮暔偼偄傢備傞僔儏僞僀僫乕揰偵杽傑偭偰偄傞偲巚偄傑偡
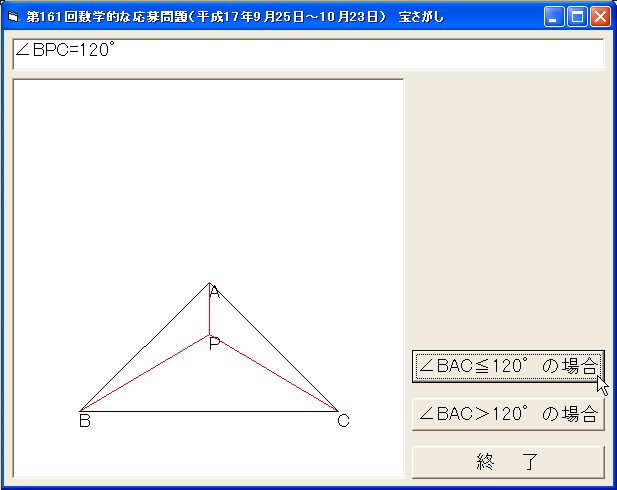
僔儏僞僀僫乕揰偼佢APB亖佢BPC亖佢CPA亖侾俀侽亱偲側傞揰偩偐傜丂P偼BC偺悅捈擇摍暘慄忋偺丄佢BPC亖侾俀侽亱偲側傞揰偱偡
佢PBC亖佢PCB亖俁侽亱偲側傞揰偲偄偭偰傕偄偄偐偲巚偄傑偡丂佢BAC亖侾俀侽亱偺帪偼P亖A偲側傝傑偡
仸擇摍曈嶰妏宍偺帪偼丂B偲C偺埵抲偑寛傑傟偽A偺埵抲偵娭學側偔P偼掕傑傞傫偱偡偹両
仸僔儏僞僀僫乕揰偵偮偄偰偼丂埲慜偵uchinyan偝傫偵徹柧傕娷傔偰偔傢偟偔嫵偊偰偄偨偩偒傑偟偨
NO8乽Toru乿丂丂10/05 15帪59暘庴怣 峏怴10/23丂
戞侾俇侾夞栤戣偺夝摎傪憲傝傑偡丅僼僃儖儅乕偺栤戣偱丄幚偼慜偵傕尒偨偙偲偑偁傝傑偟偨丅偄傠偄傠側夝朄偑偁傞傛偆偱偡偑丄幚嵺丄夝摎傪彂偙偆偲偟偰傒傞偲丄
120搙偱応崌暘偗偟偨帪偵丄摑堦揑偵埖偆偲偙傠偑偳偆傕崱堦偮偱抶偔側傝傑偟偨丅
丂
堦斒偺儮ABC偺奺捀揰傊偺嫍棧偺榓偑嵟彫偲偄偆偙偲偵偟偰峫偊傑偡丅
丂嶰妏宍偺奜晹偺揰E偵偮偄偰偼丄EA or EB or EC 偑曈BC,CA,AB偵岎傢傞帪偼E傪偦偺岎揰偵堏摦偝偣傞丅偳傟傕岎傢傜側偄帪偼丄偄偢傟偐偺捀揰偵堏摦偝偣傞
乮偨偲偊偽佢BEC亜佢BEA,佢AEC側傜揰A傊乯偙偲偱丄傛傝彫偝偔偱偒傞偺偱丄彍奜偟偰傛偄丅
丂
丂儮ABC偱佢A亞佢B,佢C偲偟偰丄偙偺撪晹偁傞偄偼廃忋偺堦揰P傪偲傞丅儮ABP傪A傪拞怱偵60搙,帪寁曽岦偵夞揮偝偣偰儮AB'P'偲側偭偨偲偡傞偲丄愜傟慄B'P'PC偼B'AC偺儮ABC懁偵偁傝丄儮BPP'偑惓嶰妏宍偱偁傞偙偲偐傜丄AP+BP+CP=B'P'+P'P+PC
丂
丂佢A亙120搙偺帪丄惓嶰妏宍AB'B偺奜愙墌偲B'C偺岎揰(B'帺恎偲偼堎側傞曽偺乯偼儮ABC偺撪晹偵偁傝丄偙偺揰傪P偲偡傟偽丄墌廃妏偐傜佢APB'=佢ABB'=60搙傛傝丄
B',P',P,C偑堦捈慄忋偵側傜傃丄偙偺帪AP+BP+CP=B'P'+P'P+PC=B'C偱嵟彫偲側傞丅
偙偺帪佢APB=佢BPC=佢CPA=120搙
丂
丂佢A=120搙 偺帪丄偙偺揰偼A偵堦抳偡傞丅
丂
丂佢A亜120搙偺帪丄B'A傪墑挿偟偨揰偲愜傟慄B'P'PC偺岎揰傪Q偲偟偰丄愜傟慄偺偆偪B'Q傪捈慄B'Q偵抲偒姺偊丄師偓偵愜傟慄AQC傪捈慄AC帡抲偒姺偊傞偙偲偵傛偭
偰AP+BP+CP=B'P'+P'P+PC亞B'A+AC=BA+AC
乮A偺偲偙傠偵偔偄偑懪偭偰偁偭偰丄B'乣C傊巺傪挘傞僀儊乕僕偱偡丅乯摍崋偼P=A偺帪丅丂丂
![]()
