�ߘa�Q�N�U���V��
 [���ꐯ]
[���ꐯ]
�@�@�@�@��386�����w�I�ȉ����
�@�@�@�@����W���ԁF5��10���`6���V����
�m��{���[�Z�z3�n
�@��384�����瑱���Ă��܂�
�@��385�����瑱���Ă��܂�
�@ ��X���@
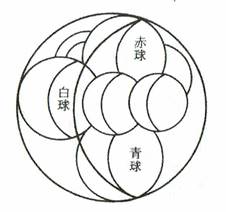
��X���@
�����ɐԋ��A�������A���̌��ԂɂT�̋�����ɓ����(���݂ɐڂ���悤��)�B�ԋ��a�A���a��m���ĊO���a�����߂�B

�����̗���F��@�͋��߂܂��A�������E�E�E��
 ��10���
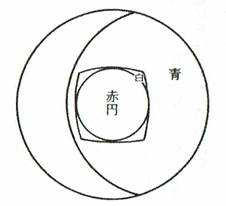
��10���
�ʂɔ������`�������A���̓��ԉ~��������i�~���̎��͐��̒��S��ʂ�j�B���a�Ɛԉ~�a�����ꂼ��m���Đ����Ȗʐς����߂�B
�@�ȉ��͌����ł��B
��\���
���L�@�������`�������e�Ԛ��ہi�����`�M�S�����S�j
���]���l����l�������ۖʏp�@��
�@���H�ˍ��p����
�p�H�ȋ��l�����l�����V�[���Ȉ��@�[���l�ˌʏp�����w�担�l�Г����ۖʐύ���
�����̗���F�p����ǂł����A��@���������B���̕s�����l�����܂��̂ŁA��@�����߂܂���B�@�������A�o�T�ɂ�������@���ڂ��Ă����܂��B��

 ��11���
��11���
�Q�̉~������ō��A���A�̂R�~�Ɖ��~��������i���ɂV�Ƃ��A�݂��ɊO�ڂ��Ă���j�B���a�A���a�A�a�����ꂼ��m��A���~�̌���m��Ƃ��A�����̒��a�����߂�B
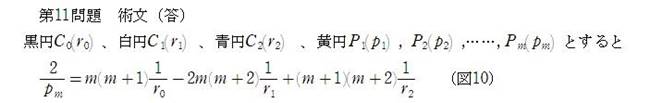
���q���g�F�f�J���g�̉~�藝�𗘗p��

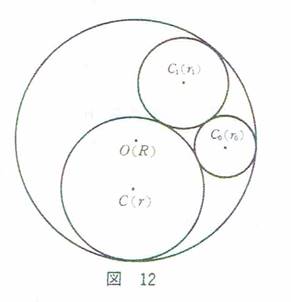
 ��12���
��12���
�Q�̉~������ō��A���A�̂R�~�Ɖ��~��������i���ɂV�Ƃ��A�݂��ɊO�ڂ��Ă���j�B���a�A���a�A�a�����ꂼ��m��A���~�̌���m��Ƃ��A�����̒��a�����߂�B


�o�T�@���̎Z�z�̉���@���؏d�V�@���@����o�Ł@
NO1�u��ӂ����̂炢��������v 05/24 08��29���@��M
�X�V 6/7
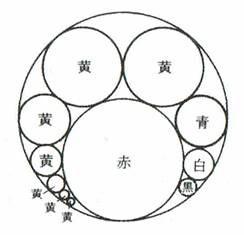
��9���
���ԋ��Ɛ��̒��S�����Ԓ�����ɋ��̒��S�͂Ȃ��Ƃ��܂��B
�i�ԋ��Ɛ��̑傫�����������ړ_�Ƌ��̒��S�������ꍇ�̐�������12���̒��ɂ���܂��j
�ׂ荇������2�Ɛ��A�ԋ��݂͌��ɐڂ��A���ɓ��ڂ���Ƃ��܂��B
3�����̏ꍇ�̃f�J���g�̉~�藝���ؖ��Ȃ��Ɏg���܂��B
���̔��a�����ꂼ�ꎟ�̂悤�ɂ����܂��B
�O�ڋ��Fr�A�ԋ��Fa�A���Fb�A����1�Fc1�A����2�Fc2�A����3�Fc3�A����4�Fc4�A����5�Fc5
�ׂ荇������2�̔��a�͓������Ȃ��Ƃ��܂��B
���O�ڋ��A�ԋ��A���A����1�A����2�ɒ藝��p����ƁA
(1/a+1/b+1/c1+1/c2-1/r)^2=3(1/a^2
+1/b^2 +1/〖c1〗^2
+1/〖c2〗^2 +1/r^2 )
{(1/a+1/b-1/r)+(1/c1+1/c2)}^2=3{(1/a^2
+1/b^2 +1/r^2 )+(1/〖c1〗^2
+1/〖c2〗^2 )}
�����ŁAA=(1/a+1/b-1/r)�AB=(1/a^2 +1/b^2 +1/r^2 )�Ƃ����A���ꂼ��̕����̋t����啶���ŕ\�����Ƃɂ��܂��B
{A+(C1+C2)}^2=3{B+(〖C1〗^2+〖C2〗^2 )}
A^2+2A(C1+C2)+(C1+C2)^2=3{B+(〖C1〗^2+〖C2〗^2 )}
A^2-3B=2{〖C1〗^2-C1C2+〖C2〗^2-A(C1+C2)}
〖C1〗^2-C1C2+〖C2〗^2-A(C1+C2)=(A^2-3B)/2 (=�萔) ⋯⋯ (�C)
���l�ɊO�ڋ��A�ԋ��A���A����2�A����3�ɒ藝��p����ƁA
〖C2〗^2-C2C3+〖C3〗^2-A(C2+C3)=(A^2-3B)/2 (=�萔) ⋯⋯ (��)
���ɔ��������ւ��āA
〖C3〗^2-C3C4+〖C4〗^2-A(C3+C4)=(A^2-3B)/2 (=�萔) ⋯⋯ (�n)
〖C4〗^2-C4C5+〖C5〗^2-A(C4+C5)=(A^2-3B)/2 (=�萔) ⋯⋯ (�j)
〖C5〗^2-C5C1+〖C1〗^2-A(C5+C1)=(A^2-3B)/2 (=�萔) ⋯⋯ (�z)
(�C)�A(��)���A
〖C1〗^2-C1C2+〖C2〗^2-A(C1+C2)=〖C2〗^2-C2C3+〖C3〗^2-A(C2+C3)
(C3-C1)C2=〖C3〗^2-〖C1〗^2-A(C3-C1)
C2=C3+C1-A
⋯⋯ (�w)
�i���j�A�i�n�j���AC3=C4+C2-A ⋯⋯ (�g)
�i�n�j�A�i�j�j���AC4=C5+C3-A ⋯⋯ (�`)
�i�j�j�A�i�z�j���AC5=C1+C4-A ⋯⋯ (��)
�i�z�j�A�i�C�j���AC1=C2+C5-A ⋯⋯ (�k)
�@�B�I�ɁA
�i�w�j�A�i�g�j���AC1+C4=2A ⋯⋯ (��)
�i�g�j�A�i�`�j���AC2+C5=2A ⋯⋯ (��)
�i�`�j�A�i���j���AC3+C1=2A ⋯⋯ (�J)
�i���j�A�i�k�j���AC4+C2=2A ⋯⋯ (��)
�i�k�j�A�i�w�j���AC5+C3=2A ⋯⋯ (�^)
�i�w�j����i�k�j�����v����Ɓi�܂��́A�i���j����i�^�j�j�AC1+C2+C3+C4+C5=5A
���̎�����A�i���j�Ɓi�^�j�������ƁAC1=A
�ϐ������Ƃɖ߂��ƁA
1/c1=1/a+1/b-1/r
1/r=1/a+1/b-1/c1
r=1/(1/a+1/b-1/c1)=1/((bc1+ca-ab)/abc1)=abc1/(bc1+c1a-ab)
����āA���a2r�́A
2r=2abc1/(bc1+c1a-ab)
To
�Ȃ�܂����A���������Č������܂��B
���i���j����i�^�j�̎��́A���锒�ʂ�3��̔��ʂƔ��a�̋t���̘a���萔�ł��邱�Ƃ������܂��B
�u1�v����3��́u4�v�ł����A�u3�v����3�悪�u1�v�ł��B
����́u1�v�����Ƃɂ���ƁA�u3�v�Ɓu4�v�̔����̔��a�����������Ƃ��Ӗ����A�O��ɔ����܂��B
���̂��Ƃ��l����ƁA��������̂Ƃ��͉�������܂���B�@
��������6�Ƃ��A���a�����ꂼ��c�Ad�Ae�Af�Ag�Ah�Ƃ���ƁA
����������1�g�̔�����p���āA
1/c+1/f=2(1/a+1/b-1/r)
2/r=2/a+2/b-1/c-1/f=(2bcf+2acf-abf-abc)/abcf=(2cf(a+b)-ab(f+c))/abcf=(2c(a+b)-ab(1+c/f))/abc
����āA
2r=4abc/(2c(a+b)-ab(1+c/f)
)
�ƂȂ�܂��B
��10���
�����̔��a��1�Ƃ��܂��B
���ʎO�p�`�̖ʐς��l���܂��B
���ʎO�p�`ABC�Ƃ́A���̒��SO��ʂ��~3�ň͂܂�镔���̂��Ƃł��B
�}�̋��ʎO�p�`ABC�Ƃ́A����ABO�A����BCO�A����CAO�ň͂܂�鏬�������̕����������܂��B
����ABO�ƕ���BCO���Ȃ��p��B�A����BCO�ƕ���CAO���Ȃ��p��C�A����CAO�ƕ���ABO���Ȃ��p��A�Ƃ��܂��B
�O�p�`ABC�ƒ��S�Ɋւ��đΏ̂̈ʒu�ɂ���O�p�`A�fB�fC�f�Ƃ͓����ʐςł��B
���a1�̋��̕\�ʐς́A4�ł��B
�}�̍��̔��œh��ꂽ�����̖ʐς́A4�~2A�^2�ł��B
�}�̍��̔����œh��ꂽ�����̖ʐς́A4�~2B�^2�ł��B
�}�̍��̔��Ԃœh��ꂽ�����̖ʐς́A4�~2C�^2�ł��B
����3�̗̈�����킹��Ƌ��̕\�ʂ����ׂĕ����܂��B
�������A�O�p�`ABC��3���A�O�p�`A�fB�fC�f��3�����Ԃ��Ă��܂��B
����āA
4��=4�~2A/2��+4�~2B/2��+4�~2C/2��-4�~∆ABC
��=A+B+C-∆ABC
����āA
∆ABC=A+B+C-��
�����A���a��R�Ȃ�ʐς�R2��������悢���ƂɂȂ�܂��B
�����Ɏl�p�`�̖ʐς��l���܂��B
��ABCD����ABC�{��CDA��(A1�{B�{C1�|��)+(C2�{D�{A2�|��)
��A�{B�{C�{D�|2��
����āA���ʐ����`�̊p�̑傫����m�邱�Ƃ��K�v�ɂȂ�܂��B
�����̔��a��R�Ƃ��܂��B
��ABCD�̂Ƃ���ɔ��aa�̉~��������܂��B
����āA��ABCD��1�ӂ�2a�ł��B�i���������j
�}�̂悤�ɁAB����OA�ɐ��������낵�܂��B(�����̑���H�Ƃ��܂�)
��OAB���o���AAH��t�Ƃ��܂��B
��ABH���Ah^2+t^2=(2a)^2
��OBH���Ah^2+(R-t)^2=R^2
�A��������ƁAt=(2a^2)/R, h=2a��(1-(a/R)^2
)
AB=2a �Ȃ̂ŁABD=2��2 a �ł��B
�O�p�`HBD�ɂ��ė]���藝��p����ƁA(��H���ƂƂ��܂�)
cos��=({2a��(1-(a/R)^2
)}^2+{2a��(1-(a/R)^2 )}^2-(2��2 a)^2)/(2�~2a��(1-(a/R)^2
)�~2a��(1-(a/R)^2
))=1-1/(1-(a/R)^2 )
����āA
��=cos^(-1){1-1/(1-(a/R)^2
)}
����āA���߂�ʐς́B
[4
cos^(-1){1-1/(1-(a/R)^2
)}-2��] R^2
��11���
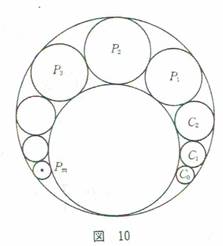
���f�J���g�̉~�藝�͏ؖ����Ȃ��Ŏg���܂��B
����Ă݂�Ƒ�ςȌv�Z�ʂɂȂ�܂��B
���O�~���A�ԉ~���A���~��0�A���~��1�ɒ藝��p����ƁA
(1/t+1/r_0
+1/r_1 -1/s)^2=2(1/t^2 +1/〖r_0〗^2 +1/〖r_1〗^2 +1/s^2 )
{(1/t-1/s)+(1/r_0
+1/r_1 )}^2=2{(1/t^2 +1/s^2 )+(1/〖r_0〗^2 +1/〖r_1〗^2 )}
(1/t-1/s)^2+(1/r_0
+1/r_1 )^2+2(1/t-1/s)(1/r_0 +1/r_1 )=2{(1/t^2 +1/s^2 )+(1/〖r_0〗^2 +1/〖r_1〗^2 )}
2(1/t-1/s)(1/r_0
+1/r_1 )=(1/t+1/s)^2+(1/r_0 -1/r_1 )^2
⋯⋯ (��)
�v�Z���y�ɂ��邽�߁A���̂悤�ɂ����܂��B
T=1/t, S=1/s, R0=1/r_0 , R1=1/r_1
����ƁA�i���j�̎��́A
2(T-S)(R0+R1)=(T+S)^2+(R0-R1)^2 ⋯⋯ (��)
���l�ɊO�~���A�ԉ~���A���~��1�A�~��2�ɒ藝��p����ƁA
2(T-S)(R1+R2)=(T+S)^2+(R1-R2)^2 ⋯⋯ (��)
���l�ɊO�~���A�ԉ~���A�~��2�A���~��1�ɒ藝��p����ƁA
2(T-S)(R2+P1)=(T+S)^2+(R2-P1)^2 ⋯⋯ (��)
�i���j�|�i���j���A
2(T-S)(R2-R0)=〖R2〗^2-2R1R2+2R0R1-〖R0〗^2
�i���j�|�i���j���A
2(T-S)(P1-R1)=〖P1〗^2-2R2P1+2R1R2-〖R1〗^2
���ꂼ��2(T�|S)�ɂ��ĉ����A�����������ƁA
(〖R2〗^2-2R1R2+2R0R1-〖R0〗^2)/(R2-R0)=(〖P1〗^2-2R2P1+2R1R2-〖R1〗^2)/(P1-R1)
(P1-R1)(〖R2〗^2-2R1R2+2R0R1-〖R0〗^2 )=(R2-R0)(〖P1〗^2-2R2P1+2R1R2-〖R1〗^2
)
(P1-R1)(R2-R0)(R2-2R1+R0)=(R2-R0){〖P1〗^2-2R2P1+R1(2R2-R1)}
R2��R0�Ƃ��āA
(P1-R1)(R2-2R1+R0)={〖P1〗^2-2R2P1+R1(2R2-R1)}
〖P1〗^2-(3R2-2R1+R0)P1+R1(3R2-3R1+R0)=0
P1��2���������Ƃ��ĉ����ƁA
P1=1/2 {(3R2-2R1+R0)�}��((3R2-2R1+R0)^2-4R1(3R2-3R1+R0) )}
�����̒��́A
(3R2-2R1+R0)^2-4R1(3R2-3R1+R0)
=9〖R2〗^2+4〖R1〗^2+〖R0〗^2-12R2R1-4R1R0+6R0R2-(12R2R1-12〖R1〗^2+4R1R0)
=9〖R2〗^2+16〖R1〗^2+〖R0〗^2-24R2R1-8R1R0+6R0R2
=(3R2-4R1+R0)^2
����āA
P1=1/2 {(3R2-2R1+R0)�}��((3R2-4R1+R0)^2 )}=1/2 {(3R2-2R1+R0)�}(3R2-4R1+R0)}
={█(1/2 (6R2-6R1+2R0)=3R2-3R1+R0@1/2 (2R1)=R1
)��
P1��R1�Ƃ��āA
P1=3R2-3R1+R0
�����l�ɊO�~���A�ԉ~���A���~��1�A�~��2�A���~��1�A���~��2�Ōv�Z����ƁA
P2=3P1-3R2+R1
�܂��~��1���炵�āA�O�~���A�ԉ~���A�~��2�A���~��1�A���~��2�A���~��3�Ōv�Z����ƁA
P3=3P2-3P1+R2
���̊W����Pm�܂ŏ������ׂ�ƁA
P1=3R2-3R1+R0
P2=3P1-3R2+R1
P3=3P2-3P1+R2
P4=3P3-3P2+P1
���
P_(m-3)=3P_(m-4)-3P_(m-5)+P_(m-6)
P_(m-2)=3P_(m-3)-3P_(m-4)+P_(m-5)
P_(m-1)=3P_(m-2)-3P_(m-3)+P_(m-4)
P_m=3P_(m-1)-3P_(m-2)+P_(m-3)
���v���Đ�������ƁA
P_m-2P_(m-1)+P_(m-2)=R2-2R1+R0(=�萔)
(P_m-P_(m-1)
)-(P_(m-1) 〖-P〗_(m-2)
)=�萔
�܂�A���̎��͊K���̊K������������ł��邱�Ƃ������Ă��܂��B
��Pm�ɂ��Ē��ׂ܂��B
P1=3R2-3R1+R0
P2=3P1-3R2+R1=3(3R2-3R1+R0)-3R2+R1=6R2-8R1+3R0
P3=3P2-3P1+R2=3(6R2-8R1+3R0)-3(3R2-3R1+R0)+R2=10R2-15R1+6R0
P4=3P3-3P2+P1=3(10R2-15R1+6R0)-3(6R2-8R1+3R0)+(3R2-3R1+R0)
=15R2-24R1+10R0
d1=P2-P1=3R2-5R1+2R0
d2=P3-P2=4R2-7R1+3R0
d3=P4-P3=5R2-9R1+4R0
e1=d2-d1=R2-2R1+R0
e2=d3-d2=R2-2R1+R0
�ȏォ��A�K��dn�̈�ʍ��́A
dn=(3R2-5R1+2R0)+(R2-2R1+R0)(n-1)
Pm�̈�ʍ��́A
Pm=(3R2-3R1+R0)+��_(k=1)^(m-1)▒{(3R2-5R1+2R0)+(R2-2R1+R0)(k-1)}
=(3R2-3R1+R0)+(m-1)/2
{2(3R2-5R1+2R0)+(R2-2R1+R0)(m-2)}
={3+3(m-1)+(m-1)(m-2)/2}R2+{-3-5(m-1)-(m-1)(m-2)}R1
+{1+2(m-1)+(m-1)(m-2)/2}R0
=1/2
(m+1)(m+2)R2-m(m+2)R1+1/2 m(m+1)R0
����āA
1/p_m =1/2
(m+1)(m+2) 1/r_2 -m(m+2) 1/r_1 +1/2 m(m+1) 1/r_0
��12���
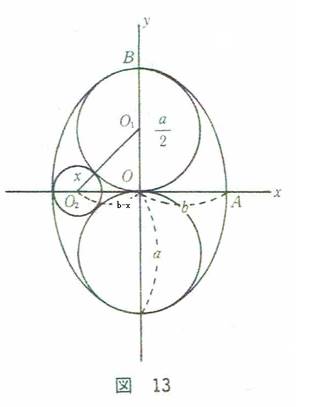
���ȉ~�̂̒��ɐԋʂ�2���ڂ��Ă���Ƃ��A���ʂ��������邩�Ƃ������Ƃ��čl���܂��B
���}�̐��́A�ȉ~���c���ɂ����Đ^�����猩�����̂ŁA
�Ԑ��́A�^�ォ�猩�����̂ł��B
�^�����猩���Ƃ��ȉ~�A�ԉ~�̕����������̂悤�ɂ��܂��B
x^2/b^2
+y^2/a^2 =1
(0<b<a)
x^2+(y-a/2)^2=(a/2)^2
���~�̔��a��t�Ƃ����܂��B
���_�A�ԉ~�̒��S�A���~�̒��S������łł��钼�p�O�p�`����A
(a/2+t)^2=(a/2)^2+(b-t)^2
t=b^2/(a+2b)
���~���S��x���Wx0��b�|t���A
x_0=(ab+b^2)/(a+2b)
����ĉ��~�̕������́A
(x-(ab+b^2)/(a+2b))^2+y^2=(b^2/(a+2b))^2
�����ɐ^�ォ�物�~�ɒ��ڂ��܂��B
�����ƌ��_��ʂ�ڐ����Ȃ��p����/2�Ƃ��܂��B
�ڐ��́A
y=tan〖��/2〗∙x
���~�Ɛڐ��̕�������A���������ʎ��ׂ܂��B
(x-(ab+b^2)/(a+2b))^2+(tan〖��/2〗 x)^2=(b^2/(a+2b))^2
〖(1+tan^2〖��/2〗 ) x^2-2 (ab+b^2)/(a+2b)
x+((ab+b^2)/(a+2b))〗^2-(b^2/(a+2b))^2=0
1/cos^2〖��/2〗
x^2-2 (ab+b^2)/(a+2b) x+(ab^2)/(a+2b)=0
D=((ab+b^2)/(a+2b))^2-1/cos^2〖��/2〗 ∙(ab^2)/(a+2b)=0
cos^2〖��/2〗=a(a+2b)/(a+b)^2
(1+cos��)/2=a(a+2b)/(a+b)^2
cos��=(a^2+2ab-b^2)/(a+b)^2 ⋯⋯ (A)
����(A)����̓I�Ɍ��Ă݂܂��B
�E����a��b��1�Ƃ��Ă݂܂��B
cos��=(a^2+2ab-b^2)/(a+b)^2
=(1^2+2∙1∙1-1^2)/(1+1)^2
=1/2
���Ɓ�60���ƂȂ�A360���^60����6���邱�Ƃ�������܂��B
�������Aa��b��0�ł͂���܂���B
�E����a��5�Ab��3�Ƃ��Ă݂܂��B
cos��=(a^2+2ab-b^2)/(a+b)^2
=(5^2+2∙5∙3-3^2)/(5+3)^2
=23/32=0.71875
>0.7071⋯=��2/2=cos〖45��〗
���A�Ƃ�45����菭���������ł��B
360���^45����8�Ȃ̂ŁA�v�Z��́A8�����ď����X�y�[�X���܂��B
�Ƃ��낪�ԉ~���ȉ~���͂ݏo���Ă��܂��܂��B
���̂��ƂׂĂ݂܂��B
�ȉ~�Ɛԉ~�̎���ό`���āA�������Ƃ����Ă݂܂��B
x^2/b^2
+y^2/a^2 =1 �� y=a��(1-x^2/b^2 )
x^2+(y-a/2)^2=(a/2)^2 �� y=a/2+��(a^2/4-x^2 )
a��(1-x^2/b^2 )=a/2+��(a^2/4-x^2 )
2a��(b^2-x^2 )=ab+b��(a^2-4x^2 )
2a��(b^2-x^2 )-b��(a^2-4x^2 )=ab
4a^2 (b^2-x^2
)+b^2 (a^2-4x^2 )-4ab��(b^2-x^2 ) ��(a^2-4x^2 )=(ab)^2
a^2 b^2-(a^2+b^2
) x^2=ab��(b^2-x^2 ) ��(a^2-4x^2 )
a^4
b^4-2a^2 b^2 (a^2+b^2 ) x^2+(a^2+b^2 )^2 x^4=a^2 b^2 (b^2-x^2 )(a^2-4x^2 )
a^4
b^4-(2a^4 b^2+〖2a^2 b〗^4 ) x^2+(a^4+2a^2 b^2+b^4 ) x^4=a^4 b^4-(a^4 b^2+4〖a^2 b〗^4 ) x^2+4a^2 b^2 x^4
-(a^4 b^2-〖2a^2 b〗^4 ) x^2+(a^4-2a^2
b^2+b^4 ) x^4=0
x^2
{(a^2-b^2 )^2 x^2-a^2 b^2 (a^2-〖2b〗^2 )}=0
x=(ab��(a^2-〖2b〗^2 ))/(a^2-b^2 )
(x>0)
�܂�Aa>��2 b �̂Ƃ��Ax��0�ȊO�ɉ������邱�ƂɂȂ�܂��B
5>��2�~3≅1.4142�~3=4.2426 �ƂȂ�܂��B
�E�ȏォ��A��������Ƃ����7�������肦�Ȃ����ƂɂȂ�܂��B
����̓I�ɒ��ׂ܂��B
a=kb �Ƃ��Ă݂܂��B
�̎��ɑ�����܂��B
cos��=(a^2+2ab-b^2)/(a+b)^2
=((kb)^2+2kbb-b^2)/(kb+b)^2 =(k^2+2k-1)/(k+1)^2
���ꂪs��cos360��/7�ɂȂ�悢�킯�ł��B
(k^2+2k-1)/(k+1)^2
=s
k^2+2k-1=s(k+1)^2
(1-s)
k^2+2(1-s)k-(1+s)=0
k=(-(1-s)�}��((1-s)^2+(1-s)(1+s) ))/(1-s)=(s-1�}��(2(1-s) ))/(1-s)
k�͐��Ȃ̂ŁA
k=(��(2(1-s) )-(1-s))/(1-s)=(��(2(1-s) )-(1-s))/(1-s)=��(2/(1-s))-1≅��(2/(1-cos〖(360��)/7〗 ))-1≅1.3047⋯
���~�̒��a�́A
2t=(2b^2)/(a+2b)=(2b^2)/(kb+2b)=2b/(k+2)=2b/(��(2/(1-s))-1+2)=2b/(��(2/(1-s))+1) (≅0.6051⋯�~b)
�u���̗���v �X�V 6/7
�����Ƒ�\���͉����Ă��܂���B




�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
