�����R�O�N�T���P�R��
 [���ꐯ]
[���ꐯ]
�@�@�@�@��359�����w�I�ȉ����
�@�@�@�@����W���ԁF4��15���`5��13����
�m��_�s�����֎��̎Z�z�n

�킪���×��̐��w�ō]�ˎ���ɔ��B�����a�Z�̖����L�ڂ����G�n�́u�Z�z�v�ƌĂ�A���w�j�����̋M�d�Ȏ����Ƃ��Đ��E�I�ɂ��S�������O���ɒ��ڂ��W�߂Ă�����̂ł���B���c�֍l�a�̗�������ޑ�_�˗̓��̈����S�O�싽�Z�����m���V�ɐĐ��F���i�ܓ����j�̖�l�����Q�V�l����[�������̎Z�z�G�n�́A���i����P�O�i�܂łP�Q�₪�A�~�`�A�O�p�`�A�H�`�Ȃǂ𑽊p�I�ɑg�ݍ��킹�A�ԁA���A���A�̍ʐF���ꂽ�w�͗l�̓�₪�u�₤�H�����X�v�u�������H�����X�v�Ɩ�薈�ɁA��������ꓚ�`���ŕ\�����Ă���A�����_���ɕ�[���A���ӂ������Ƌ��ɁA�w�K���ʂ𐢂ɃA�s�[��������ɘa�Z�����̐U�����B����������̂ł����āA����͋��炭�I�ȑ��Ƙ_���W�̂悤�Ȃ��̂ł͂Ȃ����Ɛ��@����Ĕ��܂����B
��̕��͂͊���_�s�ԍ⒬�����֎��̊��w�蕶����������p�����B
���}��1865�N�Ɍf����ꂽ�Z�z�ł��B�܂��A�����̕���͖��ԍ��ł��āA���Ȍv�炢�����Ă���B

�����ł́A��1���A��4���A��8���̌���͈ȉ��ł����A������₷�����ďo�肵�܂��B�����Ɏ���ߒ����l���Ă��������B
�Q�l�܂łɖ����֎��ɕ�[�����Z�z�̐}�̉����������Ƃŏ�������Ă��܂��B
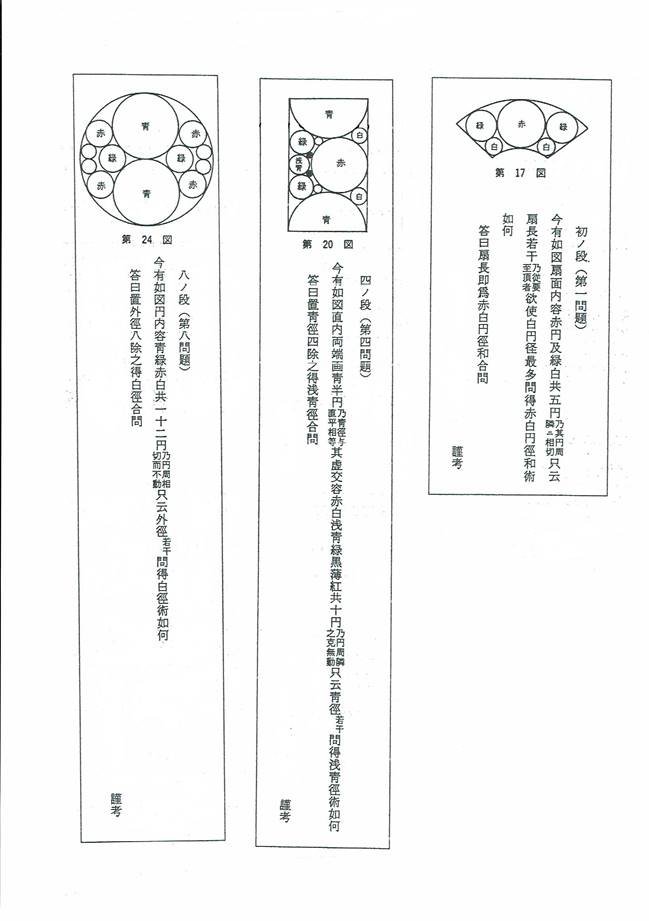
���P�D���ܐ}�̂悤�ɁA��̓��ɐԉ~�E�Ή~�E���~��5�̉~���ڂ��Ă���B��̔��a��^���Ĕ��~���ő�ɂȂ�Ƃ��A�ԉ~�Ɣ��~�̒��a�̘a�����߂�B
�@�������A��`�Ɣ��~�ƗΉ~�̒��S�͈꒼����ɂ���̂Ƃ͊��m���܂��B
�����ĞH���B�ԉ~�Ɣ��~�̒��a�̘a����̔��a
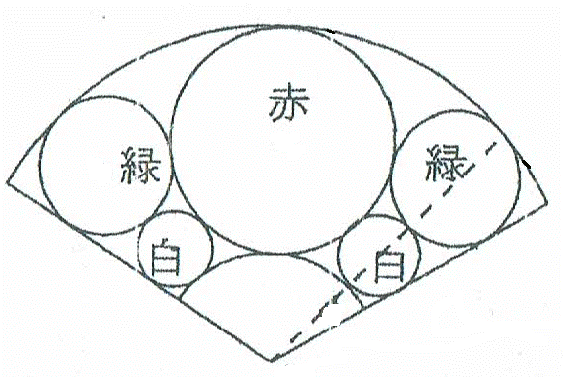
���Q�D���ܐ}�̂悤�ɁA�����`�̒��ɐ����~�i���~�̒��a�͒����`�̏c�ɓ����j������A���̊ԂɐԁE���E��E�E���E���g��10�̉~���ڂ��Ă���B�F�̉~�̒��a���^����ꂽ�Ƃ���̉~�̒��a�����߂�B
�����ŁA�~�̒��S�����L�̂悤�ɂ��܂��B

�����ĞH���B��~�̒��a���~�̒��a�^�S
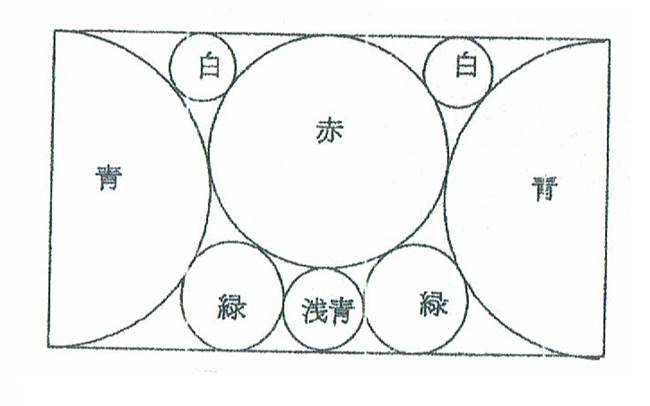
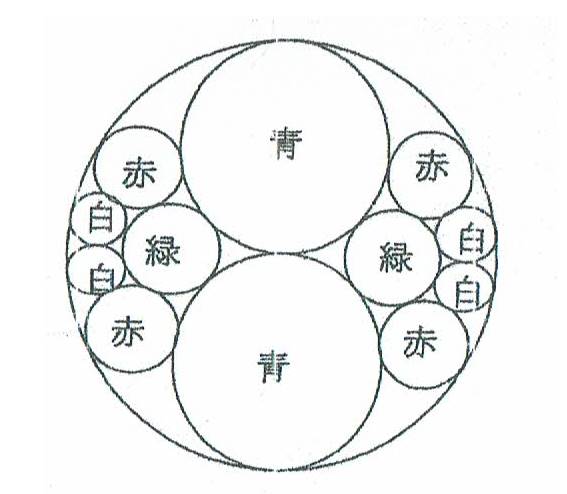
���R�D���ܐ}�̂悤�ɁA�~�̒��ɐE�E�ԁE����12�̉~�����ꂼ�ꂪ�ڂ���悤�ɗe���B�O���̉~�̒��a���^����ꂽ�Ƃ����~�̒��a�����߂�B
�Q�l�F�~�⋅�̐ڐG�����ȒP�ɉ������߂ɂ悭�g������@�����]�@�Ƃ������a�̋t�����g�����@������B�a�Z�ɂ͂��̕��@���Ȃ��A�O�����̒藝�̂悤�Ȋ�{�I�ȕ��@���g���ē���ꂽ���̂ŁA���̉͒����Ȃ�B�������A���]�@���g���Ƌɒ[�ɒZ���Ȃ�B
�����ŁA�~�̒��S�����L�̂悤�ɂ��܂��B

�����ĞH���B���~�̒��a���O���̉~�̒��a�^�W
�Q�l�����F����{�̊|��������܂����H�v �i�[��p�r�A�_���E�h���[
�����j�@�X�k�o�Ł@
�@����{�̊|��������܂����H[��][��]�v �i�[��p�r�A�_���E�h���[ �����j�@�X�k�o�Ł@
�@�@�@�@�@�Z�z�̎����͖����֎��Z�E�̌��ӂŒ����܂����B
NO1�u��x�Ђ����v 04/28 10��03���@��M
�X�V 5/13
[���1]
���}�͐�̗v(���Ȃ�)�Ɛԉ~�̒��S��ʂ钼���Ɋւ��č��E�Ώ̂Ȃ̂ŁC
���̒����̉E�����������l����D
��̔��a�� 1 �Ƃ���D�@
xy�������W���ȉ��̂悤�ɐݒ肷��D
���}�ɂ����āC��̗v�����_ O �Ƃ��C�ԉ~�̒��S R ��y����
�ɂ���CR��y���W�����ƂȂ�悤�ɂ���D
���~�̒��S W �ƁC�Ή~�̒��S G ��x���W�́C���ɐ��ƂȂ�悤�ɂ���D
�ԉ~�C���~�C�Ή~�̔��a�����ꂼ��@r�Cw�Cg �Ƃ���D
�ԉ~��y���Ƃ�2�̌�_�̂����CO�ɋ߂����� A �Ƃ���D
OA=1-2*r �ł���D
���܁C1-2*r=t*w (t �� ���̎���)�Ƃ����D
���~�ƗΉ~��3�{�̋��ʐڐ��̂����CO��ʉ߂�����̂�2�{����D
����2�{�̂����̔C�ӂ�1�{�� L �Ƃ���D
W�CG ����L�ɉ��낵�������̑������ꂼ�� B�CC �Ƃ���D
��OWB �� ��OGC �ł��邩��COW:WB=OG:GC�D
����āC(1-2*r+w):w=(1-g):g�D
����āC(t+1)*w:w=(1-g):g�D
����āC(t+1):1=(1-g):g�D
������Cg=1/(t+2)�D
(1-2*r)+2*w+2*g=1 �ł��邩��C
t*w+2*w+2*(1/(t+2))=1�D
����āCw=(t+4/t+4)^(-1)�D
���܁Ct �� t>0 �Ȃ�S�Ă͈̔͂�������̂Ƃ��āC
w=(t+4/t+4)^(-1)
�̍ő�l���l���Ă݂�D
w=(t+4/t+4)^(-1)
��(2*(t*(4/t))^(1/2)+4)^(-1) (�� (��������)��(���敽��)�C������ t=2 �̂Ƃ�����)
=1/8�D
�܂�Ct��t>0�Ȃ�S�Ă͈̔͂�������̂Ƃ���C
t=2�̂Ƃ� w�͍ő�l 1/8 ���Ƃ�D
����ɂ��̂Ƃ��C
1-2*r=t*w�Cg=1/(t+2) ���Cr=3/8�Cg=1/4 �ƂȂ�D
(w,g,r)=(1/8,1/4,3/8) �ƂȂ�悤�� ���~�C�Ή~�C�ԉ~
�����݂��邱�Ƃ��ȉ��Ɏ����D
���~�C�Ή~�C�ԉ~�̕����������̂悤�ɐݒ肷��悢�D
���~�F(x-3/10)^2+(y-9/40)^2=(1/8)^2
�Ή~�F(x-3/5)^2+(y-9/20)^2=(1/4)^2
�ԉ~�F x^2+(y-5/8)^2=(3/8)^2
�}��
�ȏ���C
��̔��a�� 1 �Ƃ����Ƃ��C ���~�̔��a�̍ő�l�� 1/8 �ł��邱�Ƃ��킩�����D
���̂Ƃ��C(�ԉ~�̒��a)+(���~�̒��a)=2*(3/8)+2*(1/8)=1=(��̔��a)
�ƂȂ��Ă���D
�܂�C��̔��a��^���Ĕ��~���ő�ɂȂ�Ƃ��C
(�ԉ~�Ɣ��~�̒��a�̘a)=(��̔��a)
�����藧�D
[���2]
�_ O �𒆐S�Ƃ���~�̔��a�� R �Ƃ���D
�_ O_i (i=1,2,3) �𒆐S�Ƃ���~�̔��a�� r_i
�Ƃ���D
2�_ O_1�CO_3 ��ʂ钼���� N �Ƃ���D
N �͒��� l�Cm �ƒ�������D
�_ O ���� m �ɉ��낵�������̑��� H
�_ O ���� N �ɉ��낵�������̑��� A �C
�_ O_2 ���� N �ɉ��낵�������̑��� B�C
�_ O_2 ���� ���� OH �ɉ��낵�������̑��� C
�Ƃ���D
2*r_1 + 2*r_3 = 2*R ----(1) �ł���D
�O�����̒藝���C
(BO_2)^2
=(O_2O_3)^2-(BO_3)^2
=(r_2+r_3)^2-(r_2-r_3)^2
=4*r_2*r_3�D
����āC
(BO_2)=2*(r_2*r_3)^(1/2)�D
�@
���l�ɍl���āC
(CO_2)=2*(R*r_2)^(1/2)�C
(AO)=2*(R*r_1)^(1/2)�D
(AB)^2+(BO_2)^2=(O_1O_2)^2 �ł���̂ŁC
(2*R-r_1-r_2)^2+4*(r_2*r_3)=(r_1+r_2)^2�D
�W�J���Đ�������ƁC
(R-r_3)*r_2=R*(R-r_1) ---(2)
AO=BO_2+CO_2 �ł���̂ŁC
2*(R*r_1)^(1/2)=2*(r_2*r_3)^(1/2)+2*(R*r_2)^(1/2) ---(3)
���܁Cr_3=(1-t)*R ---(4) (t �� 0<t<1 �Ȃ����) �Ƃ�����D
(1)�C(2)�C(4)���C
r_1=t*R ---(5)
r_2= (1-t)*R/t ---(6)
�ƂȂ�D
(4)�C(5)�C(6) �� (3) �ɑ�����C���ό`����ƁC
(1-t)^(1/2)=2*t-1�D
������ t=3/4 ��D����āCr_3=(1-3/4)*R�D
����āC2*r_3=(2*R)/4�D
�܂�C(��~�̒��a)=(�~�̒��a)/4 �ł���D
[���3]�@
xy�������W���ȉ��̂悤�ɐݒ肷��D
���}�ɂ����āC�ő�̔��a�����~�� C �Ƃ��CC �̔��a�� 1 �Ƃ���D
C�̒��S��xy�������W�̌��_ O �Ɉ�v���邷��悤�ɐݒ肷��D
�܂��C�_O_1�̍��W��x����̐��̕����ɂȂ�悤�ɂ���D
C�]�̉~�Ƃ��āC���}�]���������̂��l����D
C�̔��]�́CC ���g �ł���D
���}�ɂ����� O' �𒆐S�Ƃ���~�̔��]�́C���� y=1 �ł���D
���}�ɂ����� O'' �𒆐S�Ƃ���~�̔��]�́C���� y=-1
�ł���D
���}�ɂ����� O_i (i=1,2,3) �𒆐S�Ƃ���~�� C_i �Ƃ��C
C_i�̔��a�� s_i �Ƃ���D
C_i (i=1,2,3) �̔��]��
G_i �Ƃ���D
G_i (i=1,2,3) �́C��������~�ł���D
G_i �̒��S ����� ���a�����ꂼ��@E_i�Cr_i �Ƃ���D
G_1�̒��S��x����̐��̕����ɂ���C2���� y=1,y=-1�̗����ɐڂ���D
����� r_1=1 �ł���DG_1��C�ƌ�_�������Ȃ��D
E_2�CE_3�͂Ƃ��ɑ��ی��ɂ���D
G_2,G_3�݂͌��ɐڂ��Ă���C����ɋ��ɁCC��G_1�̗����ɐڂ���D
G_3��x���ɐڂ��Ă���CG_2��y=1�ɐڂ��Ă���D
����E_2E_3��x���ƒ�������D
�ȏ���l������ƁC���]���ꂽ�}�`�̐ڐG�W�͈ȉ��̐}�̂悤�ɂȂ�D
�}���C2*(r_2 + r_3)=1 --- (1)
E_2�CE_3 ���� y���ɉ��낵�������̑��� H_2�CH_3 �Ƃ���D
�O�����̒藝���C
(E_2H_2)^2=(OE_2)^2-(OH_2)^2=(1+r_2)^2-(1-r_2)^2=4*r_2.
(E_3H_3)^2=(OE_3)^2-(OH_2)^2=(1+r_3)^2-(r_3)^2=1+2*r_3�D
(E_2H_2)^2=(E_3H_3)^2 �ł��邩��C4*r_2=1+2*r_3 --- (2)
(1)�C(2)���Cr_2=1/3�Cr_3=1/6 ��D
������ OE_3 �� G_3 �Ƃ�2�̌�_���CO�ɋ߂������� M'�CN' �Ƃ���D
OM'=1�CON'=1+2*r_3 �ł���D
���]�ɂ���āCM �� M'�ɁCN �� N'�� ���ꂼ�� �ϊ����ꂽ�Ƃ���D
(C_3�̒��a)=NM=OM-ON=1/OM'-1/ON' �ł���D
����āC
s_3
=(1/2)*(1/OM'-1/ON')
=(1/2)*(1-1/(1+2*r_3))
=(1/2)*(1-1/(1+2*(1/6)))
=1/8.
����āC(���~�̔��a)=(�O���̉~�̔��a)/8�D
�܂�C(���~�̒��a)=(�O���̉~�̒��a)/8 �ƂȂ��Ă���D
���l�ɍl���āCs_2�Cs_1 ���v�Z�ł���D
s_2
=(1/2)*(1-1/(1+2*r_2))
=(1/2)*(1-1/(1+2*(1/3)))
=1/5�D
s_1
=(1/2)*(1/(2*(E_2H_2)-1)-1/(2*(E_2H_2)+1))
=(1/2)*(1/(4*3^(-1/2)-1)-1/(4*3^(-1/2)+1))
=3/13�D
�ȏ�D
NO2�u���N���̂�������v 05/05 16��02���@��M �X�V 5/13
359�@���N���̂�������
���1
�}�̂悤�ɁA��`�̒��S�����_�A�ԉ~�̒��S��x����ɂƂ�܂��B
��`�̔��a��R�Ƃ��܂��B
�ԉ~�A�Ή~�A���~�̔��a�����ꂼ��Aa�Ab�Ac�Ƃ��܂��B
 �Ή~�A���~�̒��S�́A����y��(tan��) x�̏�ɂ���Ƃ��܂��B
�Ή~�A���~�̒��S�́A����y��(tan��) x�̏�ɂ���Ƃ��܂��B
���aR�̐�`�ɐڂ���̂ŁA
�ԉ~�̒��S��(R�|a�C0)�A
�Ή~�̒��S��((R�|b) cos���C(R�|b) sin��)
�Ƃ��܂��B
�Ή~�ɐڂ���̂ŁA
���~�̒��S��((R�|2b�|c) cos���C(R�|2b�|c) sin��)
�Ƃ��܂��B
�ԉ~�ƗΉ~���ڂ���̂ŁA
![]()
![]()
![]()
![]()
![]()
![]()
�ԉ~�Ɣ��~���ڂ���̂ŁA
![]()
![]()

![]()
![]()
(1)�A(2)���r���āA
![]()
![]()
���~�����aR�|2a�̐�`�ɐڂ���Ƃ���ƁA![]()
�����(3)�ɓ����ƁA
![]()
![]()
![]()
![]() �Ƃ��āAc �ɂ��ĉ����ƁA
�Ƃ��āAc �ɂ��ĉ����ƁA
![]()
![]()
�����a�̊�c�ƍl���܂��B(0��2a��R)
![]()
![]() �Ƃ���ƁA4(R�|2a)��R ���A
�Ƃ���ƁA4(R�|2a)��R ���A![]()
|
|
0 |
��� |
|
��� |
|
|
|
|
�{ |
0 |
�| |
|
|
|
|
���� |
�ő� |
���� |
|
�����\���A![]() �̂Ƃ��Ac���ő�Ȃ̂ŁA(4) �ɑ������ƁA
�̂Ƃ��Ac���ő�Ȃ̂ŁA(4) �ɑ������ƁA

����āA�ԉ~�Ɣ��~�̒��a�̘a�́A
![]()
�ԉ~�Ɣ��~�̒��a�̘a�́A��`�̔��a�Ɠ������Ȃ�܂��B
 ���2
���2
�}�̂悤�ɁA��������x�����d�ˁA�ԉ~�̒��S��
y����ɂƂ�܂��B
�~�̔��a��R�Ƃ��܂��B
�ԉ~�A�Ή~�A��~�̔��a�����ꂼ��Aa�Ab�Ac�Ƃ��܂��B
�~�̒��S��(p�CR)�Ƃ��܂��B
�ԉ~�́A����l�ɐڂ���̂ŁA���S��(0�C2R�|a)�A
��~�́A�������ɐڂ���̂ŁA���S��(0�Cc)
�Ƃ��܂��B
�Ή~�̒��S��(q�Cb)�Ƃ��܂��B
�~�Ɛԉ~���ڂ���̂ŁA
![]()
![]()
�ԉ~���������Ɛ�~�ɐڂ��A��~���������ɐڂ���̂ŁA
![]()
�Ή~���~�Ɛڂ���̂ŁA
![]()
![]()
�Ή~���ԉ~�Ɛڂ���̂ŁA
![]()
![]()
�Ή~����~�Ɛڂ���̂ŁA
![]()
![]()
�Ea�̏���
(2)���A![]()
(1)�ɓ���āA![]()
(4)�ɓ���āA![]()
�Ep�̏���
(1.1)���A![]()
(3)�ɓ���āA![]()
�Eq�̏���
(5)���A![]()
(3.1)�ɓ���āA![]()
(4.1)�ɓ���āA![]()
�Eb�̏���
(4.11)���A![]()
(3.11)�ɓ���āA![]()
��������ƁA![]()
�܂�A��~�̒��a�́A�~��4����1�ł��B
�����3�Ŏg���̂ŁAp�̒l���v�Z���Ă����܂��B
c�̒l��(2)�ɓ���āA![]() �A�����(1)�ɓ���āA
�A�����(1)�ɓ���āA![]() �ł��B
�ł��B
���3
 �}�̂悤�ɁA2�̐~�̐ړ_�����_�ɁA2��
�}�̂悤�ɁA2�̐~�̐ړ_�����_�ɁA2��
���~�̐ړ_��x����ɂƂ�܂��B
�O�~�̔��a��R�Ƃ��܂��B
�~�̔��a��R/2�ł��B
�Ή~�A�ԉ~�A���~�̔��a�����ꂼ��Aa�Ab�Ac�Ƃ��܂��B
�~�̒��S��(0�CR/2)�Ƃ��܂��B
�Ή~�̒��S��(p�C0)�Ƃ��܂��B
�ԉ~���O�~�ɐڂ���̂ŁA���S��
((R�|b)cos���C(R�|b)sin��)�Ƃ��܂��B
���~���O�~�ɐڂ���̂ŁA���S��
((R�|c)cos���C(R�|c)sin��)�Ƃ��܂��B
�Ή~�Ɛ~���ڂ���̂ŁA
![]()
![]()
�ԉ~���~�Ɛڂ���̂ŁA
![]()
![]()
![]()
![]()
�ԉ~���Ή~�Ɛڂ���̂ŁA
![]()
![]()
![]()
���~���Ή~�Ɛڂ���̂ŁA
![]()
![]()
![]()
���~��x���Ɛڂ���̂ŁA
![]()
���~���ԉ~�Ɛڂ���̂ŁA
![]()
![]()
![]()
![]()
�Ep�̏���
(1)���A![]() �A
�A![]()
(3)�ɓ���āA
![]()
![]()
(4)�ɓ���āA
![]()
![]()
�E���̏���
(2)�A(3.1)���A
![]()

���A
![]()
�E���̏���
(5)��(4.1)���A
![]()
![]()
���A
![]()
�E(6)�Ɋe�O�p���̒l�������āA
![]()
![]()
![]()
���A
![]()
(8)���A
![]()
![]()
![]() �Ȃ̂ŁA
�Ȃ̂ŁA
![]()
(7)���A
![]()
(8.1)�����āA
![]()
![]()
![]()
![]()
![]() �Ȃ̂ŁA
�Ȃ̂ŁA
![]()
(9)���A
![]()
![]()
![]() �Ȃ̂ŁA
�Ȃ̂ŁA
![]()
����ɁA(8.1)�A(7.1)�����āA
![]()
![]()
![]()
![]()
![]()
![]()
![]() �Ȃ̂ŁA
�Ȃ̂ŁA
![]()
���~�̒��a�́A�O�~�̒��a��8����1�ł��B
����{�I�ȕ��@�ł̉́A��ςȂ��Ƃ��킩�����̂ŁA���]�@������Ă݂܂��B
���̐}�̂悤�ɁA�O�~�Ɛ~1�Ƃ̐ړ_�]�̒��S�Ƃ��܂��B
���]�̒��S����̋����̋t���̒l���L���Ă����ƁA�~1�ƊO�~�̉~���͒����ɂȂ�܂��B
���]�̒��S��ʂ�Ȃ��~�́A���]�̒��S��ʂ�Ȃ��~�ɂȂ�܂��B
�~2�Ɛԉ~1�̓�́A�~1�ƊO�~�ɐڂ��Ă���̂ŁA�E�̐}�̂悤��2�����ɐڂ���~�ł��B
�ԉ~1�E���~1�E���~2�E�ԉ~2�́A��������O�~�ɐڂ��A���ԂɌ݂��ɐڂ���̂ŁA�E�̐}�̂悤�ɂȂ�܂��B
�Ή~�́A�ԉ~1�E���~1�E���~2�E�ԉ~2�ɐڂ��A���~1�E�~2�ɐڂ���̂ŁA�E�̐}�̂悤�ɂȂ�܂��B
�����ŕ�����̂́A���]�����}�́A���2�̐}�Ɠ������Ƃ������Ƃł��B

 ���āA���]�̐}�̊̐S�ȂƂ���������܂��B
���āA���]�̐}�̊̐S�ȂƂ���������܂��B
���]�̒��S��O�A���~2�̒��S��Q�A
���]��̔��~2�̒��S��Q�f�Ƃ��܂��B
���~2��Ŕ��]�̒��S��ʂ钼�����2�_A�AB��
���ꂼ��A�f�AB�f�ɔ��]�����Ƃ��܂��B
![]() �Ƃ���ƁA
�Ƃ���ƁA
![]() ���A
���A![]() �Ȃ̂ŁA
�Ȃ̂ŁA
![]() �ł��B
�ł��B
��OQA�䁢OQ'B'�Ȃ̂ŁA���ׂ��̒藝���A
���a�̒����̔�̒l�́A
![]()
����āA
![]()
����܂��āA�v�Z���܂��B
���Ƃ��Ƃ̊O�~�̔��a��R�Ƃ���ƁA�O�~�̒��a��2R�ł��B
�~1�̒��a�́AR�ł��B
����ƁA���]�̒��S���甽�]��̊O�~�����������A�~1�����������܂ł̋����͂��ꂼ��A1/2R�A1/R�ł��B
���]��̐~1�̔��a�́A![]() �ł��B
�ł��B
���̒l�����ƂɁA���2�̌��ʂ�p����ƁA���]��̔��~1�̔��a�́A![]() �B
�B
�}��HQ'�̋�����p�̒����ɂ�����̂ŁA![]() �B
�B
�ȏォ��A
![]()
![]()
�䂦�ɁA

���~�̔��a�́A�O�~�̔��a��8����1�ɂȂ�܂��B
�܂�A���~�̒��a�́A�O�~�̒��a��8����1�ł��B
�����]�@�́A���S���~����ɂ���A���̉~�������ɔ��]�����̂ł��̕����͂��₷���Ȃ�܂��B
�������A���S��ʂ�Ȃ������́A�~�ɔ��]�����̂ł��̕����͂��ɂ����Ȃ邱�Ƃ�����܂��B
�����̗���F�����֎��Z�E���������������̉ł��B��
���P

���Q

���R


���Q�����̗���̉�@��
�藝�@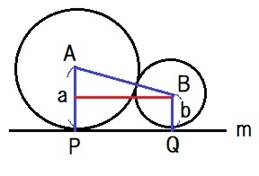 ���a��a�A����2�̉~�`�Ƃa���݂��ɊO�ڂ��A�蒼�����ɂ��ꂼ��_�o�Ƃp�Őڂ��Ă���B
���a��a�A����2�̉~�`�Ƃa���݂��ɊO�ڂ��A�蒼�����ɂ��ꂼ��_�o�Ƃp�Őڂ��Ă���B
���̂Ƃ��A�i�o�p�j�Q���S�����ł���B
�ؖ��@�Q�̉~�̐ړ_��ʂ钆�S���`�a���ΕӂƂ��钼�p�O�p�`�ɎO�����̒藝��p����ƁA
�i�o�p�j�Q�{�ia�\���j�Q���ia�{���j�Q�@���
�@�@�i�o�p�j�Q���S�����@�@��B
���}�̂悤��4�̉~���n(��)�A�n�P(a)�A�n�Q(��)�A�n�R(��)�Ƃ��A
�Q�̒��p�O�p�`�n�P�n�Q�o�Ƃn�n�P�p�����B
���炩�ɂ��{�������ł���B
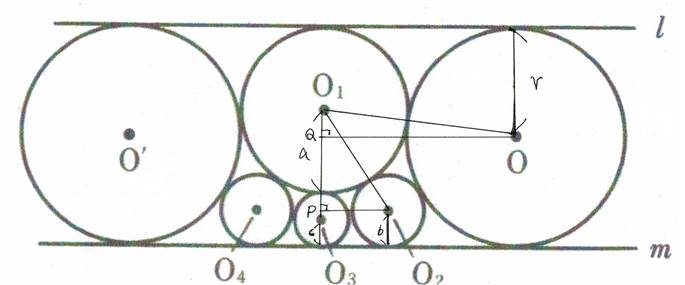
���p�O�p�`�n�P�n�Q�o�ŎO�����̒藝��p����ƁA
�ia�{���j�Q�\{�Q��(����)}�Q���i�Q���|a�\���j�Q�@���ia�{�Q���\���j�Q
�@�@�̂Ɂ@�����i���Q�{�����j�^���E�E�E�E�@
�܂��A���p�O�p�`�n�n�P�p�ŎO�����̒藝�ƑO�q�̒藝����
�ia�{���j�Q���i���\a�j�Q�{{�Q��(����)�{�Q��(����)}�Q
�W�J��@�@�������@�������\����p���ā@���Ƃ��̕����������A�����������������
�����S������B
���R�����̗���̉�@��
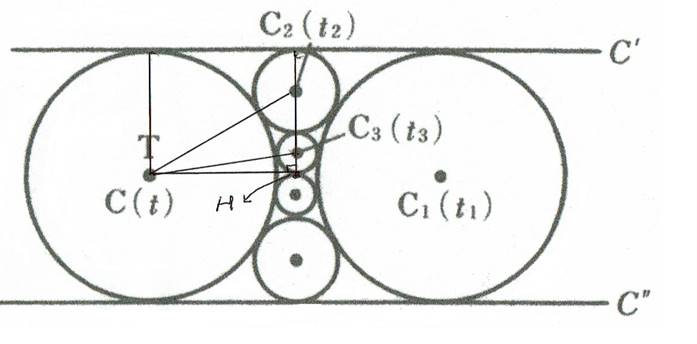
�@2�̉~�n�f�Ƃn�g�̐ړ_���s�Ƃ��A�����Ŕ��a�P�̉~�ɔ��]����ƁA���̂Ƃ��A���ŗ^����ꂽ�}�͉��}�̂悤�ɂȂ�B�~�n(��)�̔��]���b(��)�A�~�n�f(��)���b�e�A�~�n�h(��)���b�g�A
�~�ni(��i)�̔��]���bi(��i)�@�ii���P�C�Q�C�R�j�ƕ\���Ă���B���]���ꂽ�}����A
�����Q���Q�{�Q���R
���p�O�p�`�b�b�R�g�ŎO�����藝�Ɩ��Q�ŏq�ׂ��藝����
�Q��(�����Q)����{�i���{���R�j�Q�|���R�Q}����{�i���{���Q�j�Q�|�i���Q�{�Q���R�j�Q}
����������āA���Q�����^�R�C���R�����^�U�@����B�������A�����P�^��
���ɁA���]�̒��S�ł���_�s����~�b�R(���R)�Ɏ���ڐ��̒����k�͖��Q�ŏq�ׂ��藝����
�k���Q��(�����Q)�ł���B
�����ŁA���]�@�̒��ɂ����y�藝D�z
�@���]�̒��S T ��ʂ�Ȃ����a r �̉~ C �����a ��' �̉~ C' �ɔ��]�����Ƃ��A�_ T ����~ C' �ւ̐ڐ��̒����� L
�Ƃ���ƁA���̓��������藧�B
r = r' k2 / L2
��p���āA���̏ꍇ�͔��a�P�̉~�Ŕ��]���Ă��邩��A�j���P�ł���B
���R�^���R���k�Q�@�@�̂Ɂ@���R���P�^(�W��)�����^�W�@�I���
�lj��A�����悤���y�藝D�z��p���āA
���]�̒��S�ł���_�s����~�b�Q(���Q)�Ɏ���ڐ��̒����k�Q�͎O�����̒藝����
�k�Q���i���{���Q�j�Q�|���Q�Q�����Q�{�Q���Q���@���A
���Q�^���Q���k�Q�����Q�{�Q���Q���@
����āA���Q���P�^(�T��)�����^�T�@
�܂��A���]�̒��S�ł���_�s����~�b�P(���P)�Ɏ���ڐ��̒����k�Q�͎O�����̒�Ɨ����Q�ŏq�ׂ��藝����A�܂��}���炔�����P����
�k�Q���i�Q��(�����Q)�{�Q��(���P���Q)�j�Q�|���P�Q�@���P�U���P���Q�|���P�Q
���P�^���P���P�U���P���Q�|���P�Q
����āA���Q���R�^(�P�R��)���i�R�^�P�R�j���@�@
NO3�u�W���J�[�v �ߘa3�N03/26 15��07���@��M
�X�V�@�ߘa3�N 3/27
���������b�ɂȂ��Ă��܂��u�W���J�[�v�����ꂽ���Q�������B
�u�W���J�[�v �ߘa3�N04/13 19��06���@��M �X�V�@�ߘa3�N 4/15
�u�W���J�[�v�����ꂽ���1�Ɩ��R�������B
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
