�ߘa�Q�N�W���R�O��
 [���ꐯ]
[���ꐯ]
�@�@��389�����w�I�ȘA�������
�@�@�@�@����W���ԁF8��2���`8��30����
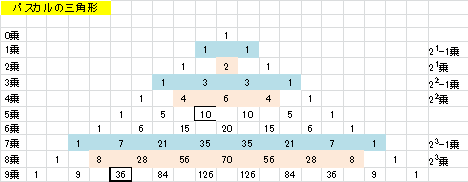
�m�W���n
�W���Ƃ�(1 + x)n ���W�J�ɂ����� xk �̍��̌W���̂��Ƃł��B�������C���i�O���������j�i���C���͐����j�ƕ\���܂��B
���P�@�W����C�������ׂĊ�̂Ƃ��́A���͂ǂ�Ȑ������B
���Q�@�W���R�W�RC�������߂ċ����ƂȂ邋�����߂�B
���R�@���{�P���Q�i�@�ŕ\�����Ƃ��A
�W����C�������߂ċ����ƂȂ邋���l�@���Ă��������B
�lj����i�ҁ@�W���[�J�[����j
�l�p�`ABCD�͉~�ɊO�ڂ��C�}�̂悤�ɐړ_��E�CF�C
G�CH�Ƃ��CAE=a�CBF��b�CCG=c�CDH��d�Ƃ���B
�}�̂悤�ɁC�l�p�`�̕ӂ��邢�͂��̉����ɐڂ���
4�̉~�̒��S�����ꂼ��P�CQ�CR�CS�Ƃ���Ƃ��C
(�l�p�`PQRS)/(�l�p�`ABCD)�̒l�����߂�B
�}�͂������N���b�N���������B
�̂Ƃ��A���̐}�𗘗p���Ă�������
NO1�u�X���[�N�}���v 08/06 20��53���@��M
�X�V 8/30
���P�@�W����C�������ׂĊ�̂Ƃ��́A���͂ǂ�Ȑ������B
nCk
=n*(n-1)*(n-2)*�c*(n-(k-1))/{k(*k-1)*(k-2)*�c*2*1}
����A���q�ɂ͂��ꂼ��k�̐�������A�����͌��݂ɕ���
�ǂ�k�ł�nCk�͊�Ȃ̂Łc
����ƕ��q��2�̌��������ł�������c
�ǂ̋����ɂȂ鍀��2��������ɂȂ�Ζ������c
�����łȂ��ƁAn>=k�Ȃ̂ŁA���q��2^2�Ƃ�2^3�Ƃ��]���Ɏc��\�����o�Ă��邩��B
so�c
n=2^m-1 �ł�������B
���Q�@�W���R�W�RC�������߂ċ����ƂȂ邋�����߂�B
���q�̕���������2�̌������߂đ傫���Ȃ�Ƃ��c
k��2^x�ŁA2k�܂�2^(x+1)��383-k+1�ƂȂ�Ƃ��c
256=2^8<382<2^9=512
so�c(383-k+1)=256=2^8
so�ck=2^7=128
���ۂɁA384-256=128=2^7=k
���R�@���{�P���Q�i�@�ŕ\�����Ƃ��A
�W����C�������߂ċ����ƂȂ邋���l�@���Ă��������B
�Ӗ����悭�킩��܂��A
���1����An��2^m-1
���2����A
�E2^x<=n<2^(x+1)�̂Ƃ��c
�@k=1
�E2^x<n<2^(x+1)�̂Ƃ�...
k=2^x/2=2^(x-1)
NO2�u�W���[�J�[�v �@
08/26 09��33���@��M �X�V 8/30
�u�W���[�J�[�v �@ 08/26 09��33���@��M �X�V 8/30
�u��ӂ����̂炢��������v 08/26 16��11���@��M
�X�V 8/30
���1
���悸�p�X�J���̎O�p�`�������o���܂��B
����́A(1�{x)n�̓W�J�̍��̌W����\���Ă��܂��B
��������āA
�@ n��2k�̂Ƃ��A�ŏ��ƍŌ�̈ȊO�̌W��������
�A n��2k�|1�̂Ƃ��A���ׂĂ̌W�����
�ƂȂ肻���ł��B
���悸�@���m���߂܂��B
�Ek��1�̂Ƃ��A�܂� ![]() �̂Ƃ��A
�̂Ƃ��A![]()
�ŏ��ƍŌ�ȊO�̍��̌W���������ł��B
�Ek�̂Ƃ��A![]() �̓W�J�̌W���́A�ŏ��ƍŌ�ȊO�������Ƃ��܂��B
�̓W�J�̌W���́A�ŏ��ƍŌ�ȊO�������Ƃ��܂��B
�@������![]() �ŕ\���ƁA
�ŕ\���ƁA
�@![]() �@�i(
�@�i(![]() )�������j
)�������j
�@���āAk�{1�̂Ƃ��́A
�@![]()
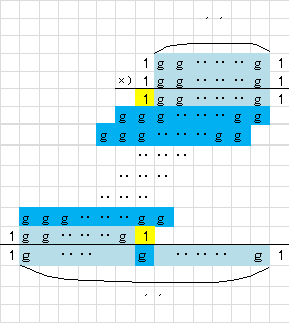
�ƂȂ�A�ŏ��ƍŌ�̈ȊO�̌W���������ƂȂ�܂��B
�����ɇA���m���߂܂��B
�Ek��1�̂Ƃ��A�܂� ![]() �̂Ƃ��A
�̂Ƃ��A![]()
���ׂĂ̌W������ł��B
�Ek�̂Ƃ��A![]() �̓W�J�̌W�����A���ׂĊ�Ƃ��܂��B
�̓W�J�̌W�����A���ׂĊ�Ƃ��܂��B
�@���d�ŕ\���ƁA
�@![]() �@�i
�@�i![]() �̊�j
�̊�j
�@���āAk�{1�̂Ƃ��́A
�@![]()
�@�܂�A![]() �Ƃ�����Ηǂ��킯�ł��B
�Ƃ�����Ηǂ��킯�ł��B
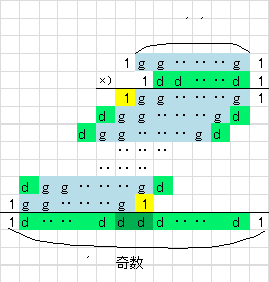
�ƂȂ�A���ׂĂ̌W������ƂȂ�܂��B
n��2k�|1�̂Ƃ��A�W��nCi�����ׂĊ�ƂȂ�܂��B
���2
���Ⴆ�Ak��6�Ƃ��Ă݂܂��B
![]()
��Ԗڂ̂Ƃ���́A���q�E����Ƃ��Ɋ�ł��B
���q�������̕���̊�ŖĂ���̂܂܂ł��B
���q�𑼂̂Ƃ���̕���̊�ŖĂ���̂܂܂ł��B
�������Ԗڂ́A���q�E����Ƃ��ɋ����ł��B
���q�E����̘a�́A384�ł��B
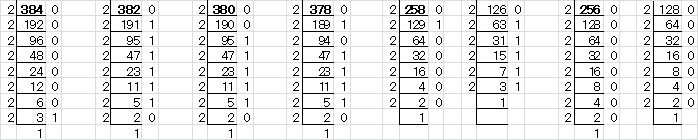
�����Ԗڂ̕��q�E����̐���2�i�@�ŕ\���Ă݂܂��B
384(10)��1,1000,0000(2)
382 (10)��1,0111,1110(2)�@�@2(10)��10(2)
380(10)��1,0111,1100(2)�@�@4(10)��100(2)
378(10)��1,0111,1010(2)�@�@6(10)��110(2)
������������
258(10)��1,0000,0010(2)�@�@126(10)��111,1110(2)
�\�\�\�\�\�\
256(10)��1,0000,0000(2)�@�@128(10)��1000,0000(2)
2�i�@�Ő���\�����Ƃ��A����0�̌�����2�̈����̌��������܂��B
382��1�A380��2�A378��1���ꂼ��2�������ɂ����܂��B
2��1�A4��2�A6��1���ꂼ��2�������ɂ����܂��B
�����q�E����̘a��384�ł��B
384(10)�́A2�i�@�ŕ\���ƁA��7����0�ł��B
�܂蕪�q�ƕ���̐��́A2�i�@�ŕ\�����Ƃ����̌���0�̌��������łȂ���0�����т܂���B
���̌�����݂Ă����āA0�łȂ��ŏ��̈ʂ́A���q�A����Ƃ���1�ł��B
�������̈ʂ́A���q�A����̈����1�ő�����0�ł��B
��������ƁA�����Ǝ��X�J���0�����Ԃ��ƂɂȂ�܂��B
���ꂪ126�̂Ƃ���܂ł͕��q�ƕ����2�̈����̌��������ł��B
�������A���̐�Ŏ���ς��܂��B
256(10)��1,0000,0000(2)�@�@128(10)��1000,0000(2)
2�������Ƃ��ĕ��q��256��8�A�����128��7�����܂��B
���Ƃ��ɁA���q�̕���2�̈������c��܂��B
�����k��128�̂Ƃ��A![]() �����߂ċ����ƂȂ�܂��B
�����߂ċ����ƂȂ�܂��B
���3
��n�������̂Ƃ��AnCk�����߂ċ����ɂȂ�̂́Ak��1�̂Ƃ��ł��B
����͕�����₷���̂ŁAn����̂Ƃ����l���܂��B
��������ƁAn�{1�͋����ƂȂ�܂��B
�E��1����0�̂Ƃ�
n�{1�́A6(10)��110(2)�A10(10)��1010(2)�A14(10)��1110(2)�A���
������2�i�@�ŕ\���Ă݂�ƁA
![]()
![]()
![]()
�̂悤�ɁAk��2��21�̂Ƃ������ƂȂ�܂��B
�E��2����0�̂Ƃ�
n�{1�́A12(10)��1100(2)�A20(10)��10100(2)�A28(10)��11100(2)�A���
������10�i�@��2�i�@�ŕ\���Ă݂�ƁA
![]()
![]()
![]()
�̂悤�ɁAk��4��22�̂Ƃ������ƂȂ�܂��B
�E��m����0�̂Ƃ�
�@���܂܂Ō��Ă����悤�ɁA2�i�@�̕����ɂ����Ƃ��A���F�̕����̕���́A
![]()
�ƂȂ�܂��B
n�{1��2�i�@�ŕ\�����Ƃ��A���̈ʂ�0�̕��т̌���m�ŕ\���A
nCk
�́A![]() �̂Ƃ��A�͂��߂ċ����ƂȂ�܂��B
�̂Ƃ��A�͂��߂ċ����ƂȂ�܂��B
�~�ɊO�ڂ���l�p�`ABCD�Ɋւ���ʐϖ��@�@�@��ӂ����̂炢��������
���܂��A��ABCD�̖ʐ�S�����߂܂��B
![]()
![]()
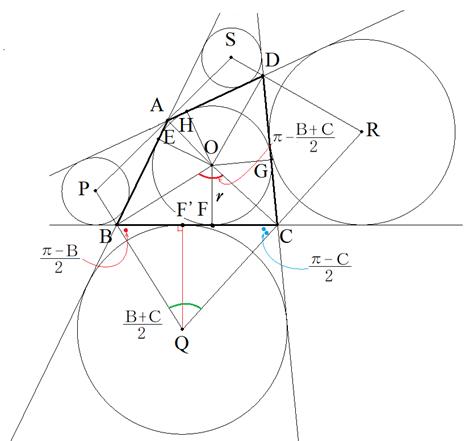
�����ɁA�~O�̔��aOF�ir�j�Ɖ~Q�̔��aOF'�����߂܂��B
��QBC�̓��p�͐}�Ɏ������ʂ�ł��B
�E��OBC�ɂ��Đ����藝���A
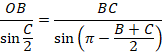
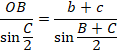
���A
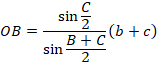
����āA
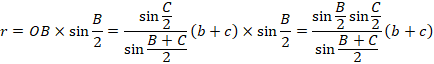
�E��QBC�ɂ��Đ����藝���A
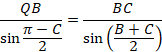
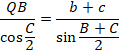
���A
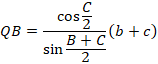
����āA
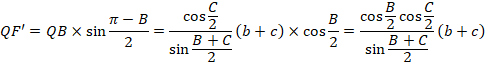
����āA
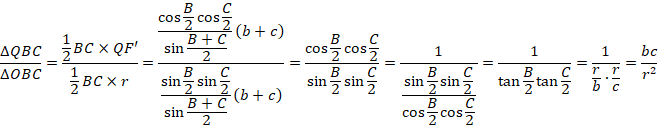
�䂦�ɁA
![]()
���l�ɁA
![]()
![]()
![]()
�����̔�����߂܂��B
![]()
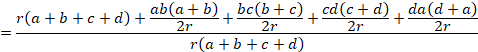
![]()
�����ŁA���낢�뒲�ׂĂ݂܂��B
������1
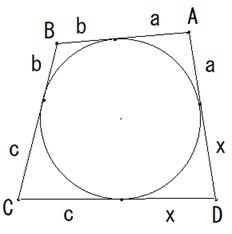
���̐}�́A����~�Ɂ�ABCD���A�O�ڂ��Ă���l�q�ł��B
�E�̐}�́A���̉~���͂����āA�ӂ̒�����ς����ɁA�l�p�`���Ԃ����l�q�ł��B
����ƁA���x���ʂ̉~�Ɂ�A'B'CD���O�ڂ��܂��B
������m���߂܂��B
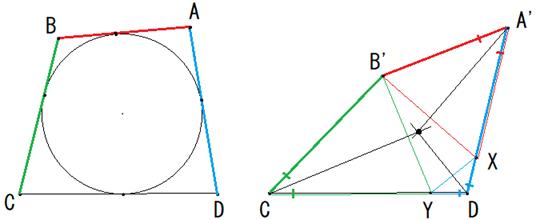
��AB���ŒZ�̕ӂƂ��܂��B
AB'��AX�ƂȂ�悤�ɁAA'D���X���Ƃ�܂��B
DX��DY�ƂȂ�悤�ɁADC���Y���Ƃ�܂��B
��A'B'X�A��DXY�A��CYB'�͓ӎO�p�`�ł��B
�~�ɊO�ڂ���l�p�`�́A����������2�ӂ̘a���������Ȃ�܂��B
�ό`�������������2�ӂ̘a���������̂ŁACB'��CY�ƂȂ�܂��B
�e�ӎO�p�`�̒��_�����ӂɐ��������낵�܂��B
����ƁA�e��ӂ͐�����2��������܂��B
��_�́A��B'XY�̊O�S�ł��B
�i3�̐�����1�_�Ō����܂��j
�e�����́A�e�ӎO�p�`�̒��p��2�������Ă���̂ŁA
��_����A'B'�܂ŁAAD�܂ŁACD�܂ŁACB'�܂ł̋������������Ȃ�܂��B
��_�𒆐S�Ƃ��A�e�ӂ܂ł̋����a�Ƃ���~���A�ʂ̉~�ɂȂ�܂��B
�l�p�`��4�ӂ̒��������܂��Ă����ډ~�̑傫���͌��܂�܂���B
������2
�l�p�`��4�ӂ̒��������_������ډ~�̐ړ_�܂łƕ�������ė^������ƁA����ς��܂��B
���̐}�ŁA���ډ~�̒��SO�́A���p��2�������Ɛړ_����̐�����ɂ���܂��B
�l�p�`��2��BC��BF�{FC��b�{c�ACD��CG�{GD��c�{d�D
���ډ~�̔��aOF��r�Ƃ��܂��B
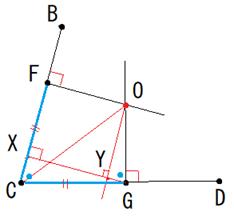
r��OF��GX�|GY��GC sinC�|OG cosC��c sinC�|r cosC
�䂦�ɁA
![]()
�i���̎��́A���p�ŕ\���Đ�������ƁA![]() �ƂȂ�܂��j
�ƂȂ�܂��j
�܂�A���p�̑傫�������܂�A���ډ~�̔��a�����܂�܂��B
�悸�A���CD���Œ肵�܂��B
���Ɂ�C�����߁ACB���Œ肵�܂��B
��(A)�ɂ��A���ډ~�̔��a�����܂�܂��B
�_B����ڐ��������āA��BA�����܂�܂��B
�Ō�ɒ��_A����ڐ��������̂ł����A���܂�D�Əd�Ȃ邩�́A������܂���B
�i�ŏ��́�C�����܂���������AD�Əd�˂邱�Ƃ��ł���͂��ł��j
������3
���̐}�ŁAOA��a�AOB��b�Ƃ��܂��B
O�ɐ��������ĂāA������̓_��AO��̓_������łł����OPP'��
��A�Ɓ�B�̕��ςł�����45���ɂȂ邱�Ƃ��l���܂��B
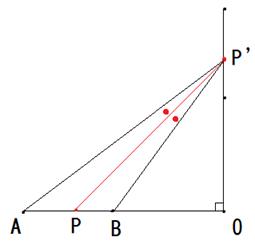
OP=OP'��r�Ƃ����܂��B
AP'�FP'B=AP�FPB �Ȃ�PP'�� ��AP'B��2��������܂��B
![]() �@
�@![]() ���A
���A![]()
![]()
�t�����Ƃ��āA
![]()
![]()
![]()
�����2�悷��ƁA
![]()
�������āA
![]()
������4
���̐}�ŁAOA��a�AOB��b�AOC��c�AOD��d�Ƃ��܂��B
O�ɐ��������ĂāA������̓_��AO��̓_������łł����OPP'��
��A�A��B�A��C�A��D�̕��ςł�����45���ɂȂ邱�Ƃ��l���܂��B
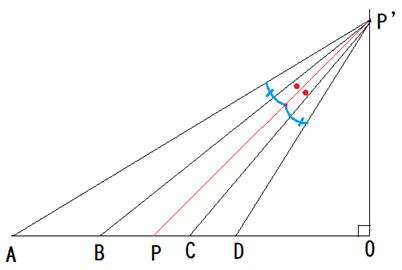
�Ead��bc�̓��ʂȏꍇ�́A![]() �ƂȂ�܂��B
�ƂȂ�܂��B
�@���̒l���A���ډ~�̔��a�ɂȂ�܂��B
�@��A�Ɓ�D�̕��ς́A![]() �̂Ƃ���ł��B�i���̓_��X�Ƃ��܂��j
�̂Ƃ���ł��B�i���̓_��X�Ƃ��܂��j
�@��B�Ɓ�C�̕��ς́A![]() �̂Ƃ���ł��B�i���̓_��Y�Ƃ��܂��j
�̂Ƃ���ł��B�i���̓_��Y�Ƃ��܂��j
�@��X�Ɓ�Y�̕��ς́A![]() �̂Ƃ���ł��B
�̂Ƃ���ł��B
�@ad=bc �Ȃ̂ŁA�_X�AY�́A����P�ł��B
����āA���̏ꍇ�́A
![]()
![]()
�E���āAad��bc�̂Ƃ��i��ʂ̂Ƃ��j�́A�܂�������܂���B
NO4�@���̗���@08/30
���P�����������ɂ���܂����B�Q�l�ɂ��Ă��������B
�@�@�@�����ɂ���������܂��B
���Q�́@���̃T�C�g�������Q�l�ɂ��ā@�o�肵�܂����B
���R�́@�����T�C�g�ɂ���܂��B
�@���l�сF�����������������Ă��܂����A���̓_�͂��e�͂��������B
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
