�ߘa�R�N11��14��
 [���ꐯ]
[���ꐯ]
�@�@��406�����w�I�ȘA�������
�@�@�@����W���ԁF10��17���`11��14����
�@�@�@�@�@�@�@�@�m�c��_�Ђ̎Z�z(4)�n

���{�V�S�{�V�����c�@�@�c��_��
�@�@�@�@�@�@�@
�c��_�Ђ̎Z�z�͓V��12�N�i1841�j����403���A��404���Ƃ���A�O���Q�N�i1845�j�Ɋ֗��a�Z�ƒJ�H�搶���E�y�����O�Y�M�`�������Z�z������B
�����405���ɑ����āA��S��A��T��ł��B
�@
�@��S���
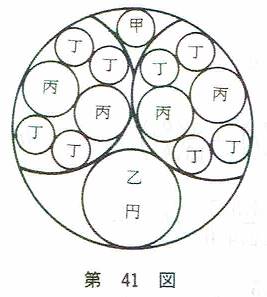 �~���ɂ��̉~�Ɠ������a�����Q�̉~�ʂ��������̒���14�̉~�������B���~�̒��a��48�{���b�~�̒��a��65�{�ɓ���������Ƃ��A���~�̒��a��m���čb�~�̒��a�����߂�B�i�}41�}�j
�~���ɂ��̉~�Ɠ������a�����Q�̉~�ʂ��������̒���14�̉~�������B���~�̒��a��48�{���b�~�̒��a��65�{�ɓ���������Ƃ��A���~�̒��a��m���čb�~�̒��a�����߂�B�i�}41�}�j

��T���
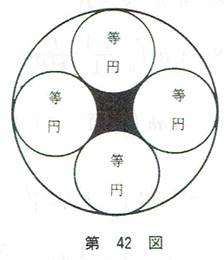
�~���ɓ��~��������i����4�j���������̖ʐςƓ��~�̒��a��m���āA���~�̌������߂�B�i��42�}�j

�p���̒����@�������́i�~�a�j���@���������̖ʐςƂ���B
�����̗���F�����̂܂܂ł͖��ɕs��������̂ňȉ��̂悤�ɉ��肵�܂���
�~���ɓ��~��������i����4�j�B�~�a�Ɠ��~�̒��a��m���āA���~�̌������߂�B�i�}42�}�j�@���@��̏p���Ƃ͌��ʂ͈Ⴂ�܂��B
�����l�сF��L�̂悤�ɏp���̒����ƍ폜�����肢���܂��B
����4�N11��16���L��
�Q�l�����@�@�@
�@�u���̎Z�z�̉���v�@���؏d���@��
�lj����i�ҁ@�W���[�J�[����j
NO1�u�X���[�N�}���v 10/17 23��05���@ ��M �X�V 11/14
�W���[�J�[�l�̖��ɍ���̓��x���W���Ă��Ƃ�!!
f(x)=(1+x+x^2+x^3)^2021
f(1)=4^2021=a0+a1+a2+�c+a6060+a6061+a6062+a6063
f(��)=1=a0+a1*��+a2*��^2+a3+�c+a6061*��+a6062*��^2+a6063
f(��^2)=1=a0+a1*��^2+a2*��+a3+�c+a6061*��^2+a6062*��+a6063
so�c
f(1)+f(��)+f(��^2)=2+4^2021=3*(a0+a3+a6+�c+a6063)
f(i)=0=a0+a1*i-a2-a3*i+a4+�c+a6060+a6061*i-a6062+a6063*i
f(-i)=0=a0-a1*i+a2-a3*i+a4+�c+a6060-a6061*i+a6062-a6063*i
so�c
3*(a0+a3+a6+�c+a6063)-4*(a0+a4+a8+�c+a6060)
=2+4^2021-0
=2+4^2021
f(i)=0=a0+a1*i-a2-a3*i+a4+�c+a6060+a6061*i-a6062-a6063*i
a6063*i�̕�����-�@�ł��B������
�����ŁA���f���̑�������������O�A�������O�@�𗘗p���Ă��������B
�����ꑧ�ł��B
3*(a0+a3+a6+�c+a6063)
=2+4^2021
��̎��͐������ł��B
NO2�u�W���[�J�[�v �@11/07
3��24��
��M �X�V 11/14
��ꂽ�c��_�Ђ̎Z�z�i4�j�̑�S��A��T��A������
�܂��A�lj���������

�u�W���[�J�[�v �ߘa4�N11/19 09��42�� ��M �X�V �ߘa4�N11/19
��T��̉����ɂ��āA���߂čl���Ă݂܂����B
�p���ŁC�u+2�v�̕����́u+3�v�̊ԈႢ�ł��邱�Ƃ��m�F�ł��܂����B
�u+2�v�ƂȂ�ƐM���C���x���ؖ������݂܂������ł��܂���ł����B
���̂��߁C���Ԃ�������������B
���M���ꂽ�c��_�Ђ̎Z�z�i4�j��T��̉����ł�����
<���̗���F�l�@������[�����ӂ��Ă��܂��B��
NO3�u��x�Ђ����v 11/11 11��49���@
��M �X�V 11/14
�lj����̉F
f(x)=(1+x+x^2+x^3)^2021
�Ƃ����D
i�������P�ʁC��=exp(2*��*i/3) �Ƃ���D
3*(a[0]+a[3]+a[6]+
�c +a[6063])-4*(a[0]+a[4]+a[8]+ �c +a[6060])
=f(1)+f(��)+f(��^2)-(f(1)+f(-1)+f(i)+f(-i))
=4^2021+1^2021+1^2021-(4^2021+0^2021+0^2021+0^2021)
=2 (��)
m��2�ȏ�̐����Ƃ���D
��=exp(2*��*i/m)
�Ƃ���D
k��m�̔{���łȂ��悤�Ȑ����Ƃ���Ƃ��C
��[j=0�`m-1](��^k)^j=0
�ƂȂ�D
�܂��Ck��m�̔{���̂Ƃ��ɂ́C
��[j=0�`m-1](��^k)^j=m
�ƂȂ�D
�ȏ�̂��Ƃ���Cx�ɂ��Ă� n ���̑�����
F(x)=A[0]+A[1]*x+A[2]*x^2+
�c +A[n]*x^n
�ɑ��āC
��[j=0�`m-1]F(��^j)���v�Z����ƁC�ȉ��̂悤�ɂȂ�D
��[j=0�`m-1]F(��^j)
=��[j=0�`m-1](��[k=0�`n]A[k]*(��^j)^k)
=��[j=0�`m-1](��[k=0�`n]A[k]*(��^k)^j)
=��[k=0�`n]A[k]*(��[j=0�`m-1](��^k)^j)
=m*(A[0]+A[m]+A[2*m]+
�c +A[floor(n/m)*m]).
(�ȏ�)
�����̗���F�l�@�܂ōl�������Ƃ͐������Ƃł��B�������Ă��܂���
NO4�u��ӂ����̂炢��������v 11/13 17��07���@ ��M
�X�V 11/14
��S���
�����̖��͂܂������Ă��܂���B
�����������Ă����܂��B
�~�̔��a��R�Ƃ��܂��B
�b�A���A���A���̉~�̔��a�����ꂼ�ꂋ�A���A���A���Ƃ��܂��B
��~�̌�_��A�AB�Ƃ��A��~�̒��S�����ꂼ��C�AD�Ƃ��܂��B
![]() �A
�A![]() �Ƃ��܂��B
�Ƃ��܂��B
�E��������A48����65���ł��B
�E���ׂ��̒藝�Ȃǂ���A
![]()
![]()
�E�}�́�ACE����A
![]()
�E�}�́�DFQ�Ȃǂ���A
![]()
![]()
��������i��ł��܂���B
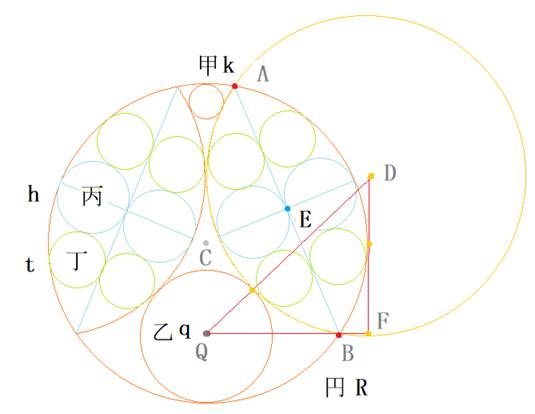
��T���
�����̖�����������Ƃ͉����Ă��܂���B
�}�Ŕ��aR�̑�~�̒��ɁA���a���̏��~�������ڂ��Ă���Ƃ��܂��B
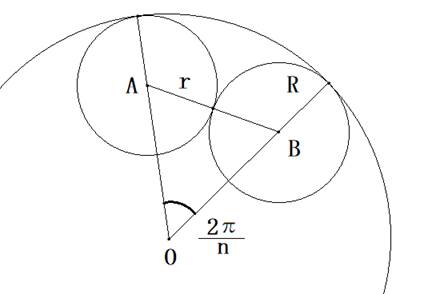
���n�`�a�ɗ]���藝��p����ƁA
![]()
![]()
![]()
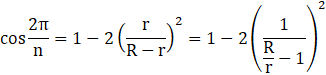
�䂦�ɁA
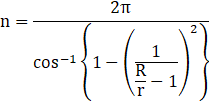
���킩��Â炢�̂ŁA�������_�ׂăv���b�g���Ă݂܂��B
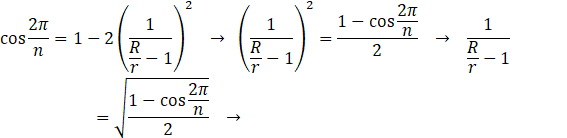
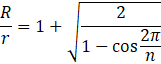
���̒l�����߁A�]���̒l�ׁAR/r�̒l�����߂܂��B
(�G�N�Z���Ɍv�Z���Ă��炢�܂���)
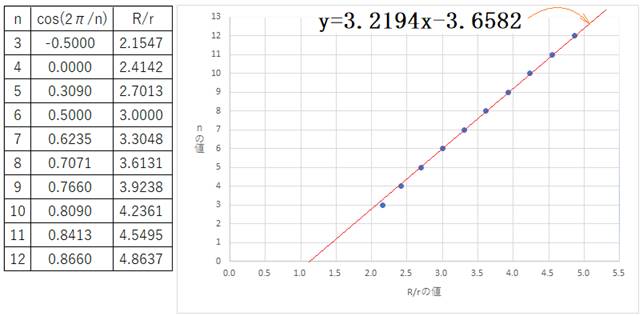
����6�Ƃ���12�̓�_�����Ԓ����������Ă݂܂��B
R/r�Ƃ��Ƃ́A1�����̊W�ł͂���܂��A
�ߎ��I�ɂ́A���̂悤�Ȏ��ŕ\���܂��B(![]() )
)
![]()
�lj����
![]()
(*)�ɂ����āA![]() �Ƃ���ƁA
�Ƃ���ƁA![]() �ł��B
�ł��B
(*)�ɂ����āA![]() �Ƃ��܂��B
�Ƃ��܂��B
![]()
(*)�ɂ����āA![]() �Ƃ��܂��B
�Ƃ��܂��B
![]()
�䂦�ɁA
![]()
������̌W���̘a�Ɗ��̌W���̘a�͓������Ȃ�܂��B
(*)�ɂ����āA![]() �Ƃ��܂��B
�Ƃ��܂��B
![]()
![]()
![]()
![]()
�䂦�ɁA
![]()
(**)�ƍ��킹�āA
4�̔{����̌W���̘a�A4�̔{���{1��̌W���̘a�A
4�̔{���{2��̌W���̘a�A4�̔{���{3��̌W���̘a
�͂��ׂē������Ȃ�܂��B
����āA![]() �ł��B
�ł��B
1��3�捪�̋�����1��![]() �Ƃ��܂��B
�Ƃ��܂��B
![]()
![]() �ł��B
�ł��B
(*)�ɂ����āA![]() �Ƃ��܂��B
�Ƃ��܂��B
![]()
![]()
![]()
(*)�ɂ����āA![]() �Ƃ��܂��B
�Ƃ��܂��B
![]()
![]()
![]()
(***)��(****)���r���āA
![]()
![]() �Ȃ̂ŁA
�Ȃ̂ŁA
![]()
![]()
���F�̕����͓������ł��B
�ΐF�̕������������Ȃ��Ƃ��̎��̒l�́A0�ɂȂ�܂���B
![]()
![]()
![]()
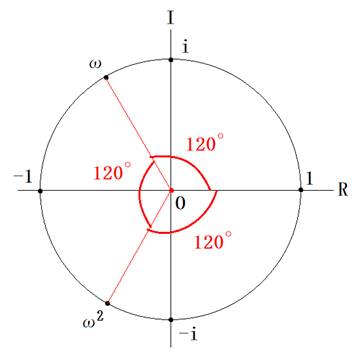
�܂�A
![]() �ł��B
�ł��B
����āA
![]()
![]()
�ȏォ��A
![]()
![]()
�����̗���F�����������@�͂��낢��ȃA�v���[�`������܂��B
�u��ӂ����̂炢��������v�̎��g�ގp���ɂ͖�������ׂ����̂�����A�����̔O���ւ����܂���B�{���ɓ���������܂��B�S���犴�ӂ̌��t�����`�����܂��B��
