�ߘa�T�N�P2���P0��
 [���ꐯ]
[���ꐯ]
�@�@��433�����w�I�ȘA�������
�@�@�@�@����W���ԁF11��12���`12��10����
�m���̕������̒l(2)�n

�lj����P�i�o��҂́u�W���[�J�[�v�j
�@��427��́u�m�����v�̖��V���[�Y�̂V��ڂł��B
�@�@
NO1�u�W���[�J�[�v �@11/16 �@�@ 21��05�� ��M �X�V 12/10
��ꂽ�����������
NO2�ukasama�v
11/19
16��19���@ ��M �X�V 12/10
��ꂽ����������
NO3�u��ӂ����̂炢��������v11/26 22��13�� ��M �X�V 12/10
�� ![]() �Ƃ��܂��B(���͐��̐����A����1�����̐��̏���)
�Ƃ��܂��B(���͐��̐����A����1�����̐��̏���)
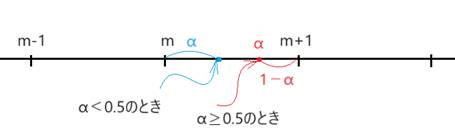
�܂�A![]() �ƂȂ�܂��B
�ƂȂ�܂��B
![]()
�E�����ŁA![]() �Ƃ��܂��B
�Ƃ��܂��B
![]()
����āA![]() �́A�݂�
�́A�݂� ![]() �ƂȂ�܂��B(��+1��)
�ƂȂ�܂��B(��+1��)
�E���l�ɁA![]() �́A
�́A
�݂� ![]() �ƂȂ�܂��B(����)
�ƂȂ�܂��B(����)
���̑����́A![]() �́A
�́A
�l��1������ ![]() �ƂȂ�܂��B(���|1��)
�ƂȂ�܂��B(���|1��)
�E�܂�A![]() ���͂���ŁA
���͂���ŁA
![]() ����
���� ![]() �܂ł�2����
�܂ł�2����![]() �ƂȂ�܂��B
�ƂȂ�܂��B
(1)
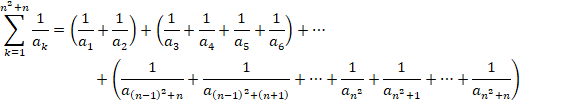
![]()
(2) 2023��44�~44�{44�{43=1980�{43 �Ȃ̂ŁA
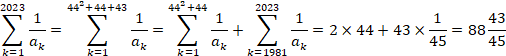
(3)�e�J�b�R�i�@�j���̍����́A�o2, 4, 6, ��� ,2n�p�ł��B
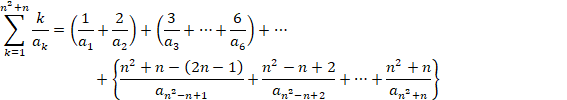
![]()
![]()
![]()
![]()
�e�J�b�R���̍��̐��́A�K�����o2, 4, 6, 8, ����p�ł��B
����āA
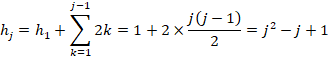
���Ԗڂ̃J�b�R�̉E�̐�![]() �́A
�́A![]() ���1�������̂ŁA
���1�������̂ŁA
![]()
����āA���Ԗڂ̃J�b�R���́A
![]()
�䂦�ɁA(1)�̒l�́A
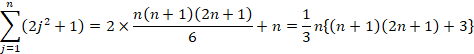
![]()
(4)
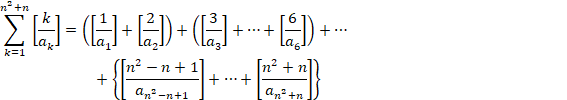
![]()
![]()
�����ŁA���Ԗڂ̃J�b�R�̒������Ă݂܂��B
![]()
![]()
![]()
�܂�A���|1��(���|�P)�A�������A1��(���{�P) �ƂȂ�܂��B
����āA(2)�́A
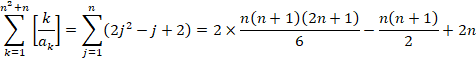
![]()
(5)
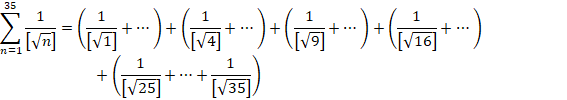
![]()
![]()
![]()
(6) ![]() �ł��B
�ł��B
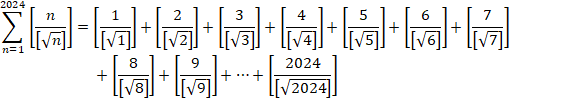
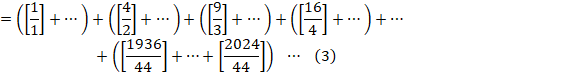
���Ԗڂ̃J�b�R�̒����݂Ă݂܂��B
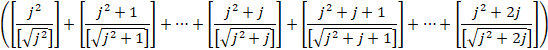
![]()
![]()
![]()
����āA(3)�́A
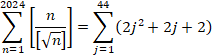
![]()
![]()
![]()
�lj����
���^����ꂽ�����������������Ƃ����̋Ȑ��ƒ�������_�������Ƃƍl���܂��B
![]()
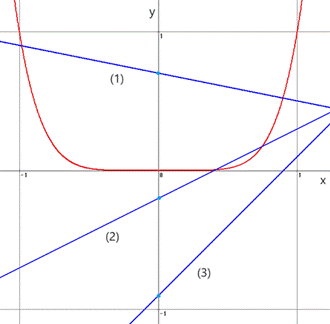
�����̂��ؕЂ� ![]() �ł���A�X��
�ł���A�X��![]() �̒l�ɂ�炸�A�������͕K���������������܂��B�i�}��1�j
�̒l�ɂ�炸�A�������͕K���������������܂��B�i�}��1�j
![]() �ł���A�����������ꍇ�Ǝ����Ȃ��ꍇ������܂��B�i�}��2�A3�j
�ł���A�����������ꍇ�Ǝ����Ȃ��ꍇ������܂��B�i�}��2�A3�j
�����������̂́A�Ȑ��ƒ����̍�D���Ƃ����Ƃ��A0�ȉ��̂Ƃ��ł��B
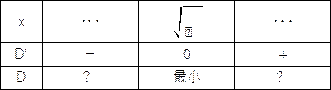
���̂����c�̎��ɂ��ǂ��ƁA
![]()
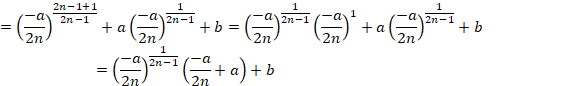
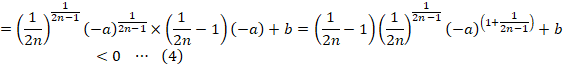
(4)��0�ȉ��ɂȂ�Ƃ����l���܂��B
�Ԃ��Ȑ� ![]() �̉����ł��B
�̉����ł��B
��̐}�́A![]() �����Ȃ̂ł����ϐ��Ƃ��܂��B
�����Ȃ̂ł����ϐ��Ƃ��܂��B
�Ȑ��́A���_��ʂ��ɊJ����V(U)���ɂȂ�܂��B
![]() �����̂Ƃ��́A��1�ی��Əc���Ώۂɕ`���܂��B
�����̂Ƃ��́A��1�ی��Əc���Ώۂɕ`���܂��B
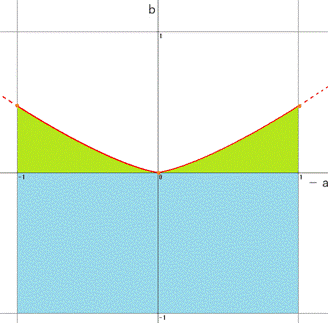
��̐}�̉��̕����̖ʐς��o���܂��B
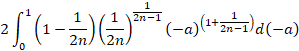
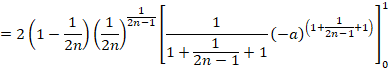
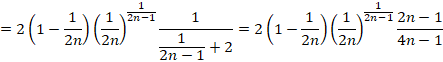
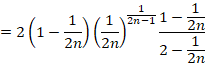
��
(1) �ȏォ��A�Ɖ��̖ʐς����킹�āA
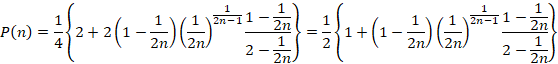
(2)
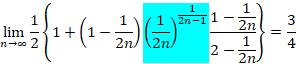
��
�����ŁA![]() ���m�F���Ă����܂��B
���m�F���Ă����܂��B
�E�悸�A![]() �ׂ܂��B
�ׂ܂��B
![]() ��1���傫���̂ŁA
��1���傫���̂ŁA![]() �Ƃ����܂��B
�Ƃ����܂��B
���́A���ɂ���Ē�܂鏬���ł��B
���ӂ�2n�|1�悷��ƁA
![]()
![]()
����āA�������̂Ƃ��A![]() �Ȃ̂ŁA
�Ȃ̂ŁA![]() �ƂȂ莦���܂����B
�ƂȂ莦���܂����B
�E����![]() �ׂ܂��B
�ׂ܂��B
![]() ��
��![]() �Ƃ́A�݂��ɋt���̊W�ɂ���܂��B
�Ƃ́A�݂��ɋt���̊W�ɂ���܂��B
![]()
����āA![]() �Ȃ̂ŁA
�Ȃ̂ŁA![]() �ɂȂ�܂��B
�ɂȂ�܂��B
�u�O�p��K�v�@�@�@�@12/09
20��28�� ��M �X�V 12/10
��ꂽ����������
�u���̗���v �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �X�V 12/10


�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���, �ƃy���l�[����Y����, ���[���ő����Ă��������B�҂��Ă��܂��B