ßaTNWPRú
 [¬ê¯]
[¬ê¯]
@@æ429ñwIÈA±åð
@@@@ðåWúÔFV23ú`W20ú
mOpÖn
âè

ÇÁâèPioèÒÍuW[J[vj
æ417ñ©çÌu³Op`ÌÓâ~ÊÉæÁÄÍÜê½}`àÌS~v
V[YÌæ10âÚªÅãÌâèÅ·B
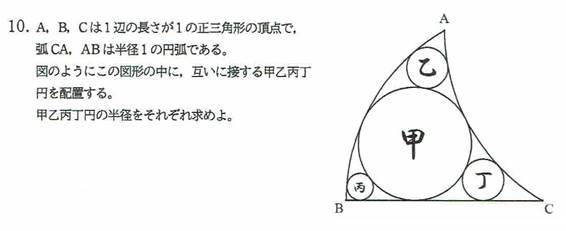
ÇÁâèQioèÒÍuW[J[vj
@æ427ñ©çÌum¦vÌâèV[YÌRâÚÅ·B
@`CaCbÌ3lªPÂ̳¢±ëð`abba`b`abba`b`abba`b`EEEÌÉ°Ä, ÅÉ1ÌÚðoµ½lð¿Æ·éB
@`CaCbªÂm¦ð»ê¼êßæB
NO1uW[J[v @07/23 @@
1620ª óM XV 8/13
uW[J[v @ 07/24 @@
0341ª óM XV 8/13
uW[J[v @ 07/25 @@
1121ª óM XV 8/13
uW[J[v @ 07/26 @@
2203ª óM XV 8/13
uW[J[v @ 07/31 @@
2248ª óM XV 8/13
ÈãÌúÉððñ¹çêܵ½B¡ñ±êçðÜÆßĩⷵܵ½Bñ¹çê½âèÌðÅ·
NOQuX[N}v 07/2V 1348ª@ óM XV 8/13
(1)
(sin(x)+2sin(y))/(cos(x)+2cos(y)+6)
f(x)=sin(x)/(cos(x)+2)Æ·éÆ
^®=f(x)@Ư¶
ff(x)=(sin^2(x)+cos^2(x)+2cos(x))/(cos(x)+2)^2
=0
2cos(x)=-1
Socx=2Î/3
Soc
Max{f(x)}=(ã3/2)/(-1/2+2)=ã3/3
(2)
(4sinÆ+2cosÆ+5)/(cosÆ+sinÆ+1)
ȺÌæ¤ÉuÆA
tan(Æ/2)=tc-Î/4<Æ<Î/2c-1<t<♾️
cosÆ=(1-t^2)/(1+t^2)
sinÆ=2t/(1+t^2)
^®=(3t^2+8t+7)/(2t+2)
((3t^2+8t+7)/(2t+2))f=(3t^2+6t+1)/(2(t+1)^2)
3t^2+6t+1=0
t=(-3-ã6)/3, (-3+ã6)/3
ãÒÌÆ«A
^®=(2t+6)/(2t+2)=(t+3)/(t+1)=6+ã6)/ã6=1+ã6
Soc
Min{^®}=1+ã6=3.449c
ÇÁâè1(Gn)
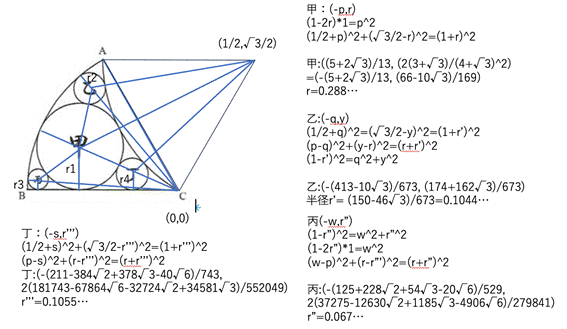
̬êF6
à éŵ½ªA4~̼aÌͳðÅ·B
ÉÍÆÄàvZªÅ«Ü¹ñBªCª±«Ü¹ñB
X[N}³ñÌvZÍÉ´ÌèÅ·
uX[N}v 08/01
2255ª@ óM XV 8/13
ÇÁâèQ
A,B,CÌÂm¦ð»ê¼ê
P(A),P(B),P(C)Æ·éÆA
P(A)=(1/6)(1+(5/6)^5)*(1/(1-(5/6)^6)
=(6^5+5^5)/(6^6-5^6)
=10901/31031
=991/2821 =0.3512c
P(B)=(1/6)((5/6)+(5/6)^4)*(1/(1-(5/6)^6)
=(5*6^4+6*5^4)/(6^6-5^6)
=10230/31031
=30/91 =0.3296c
P(C)=1-991/2821-30/91=900/2821 =0.3190c
P(A)>P(B)>P(C)
¿ÈÝÉA
ABCÌÔÌêc
P(A)+P(B)+P(C)=1
P(B)=(5/6)P(A)
P(C)=(5/6)^2P(A)
Soc
P(A)(1+5/6+(5/6)^2)=1
P(A)=6^2/(6^2+6*5+5^2)=36/91
P(B)=30/91
P(C)=25/91
̬êFððϦÄÌl@ èªÆ¤²´¢Ü·B
NO3ukasamav
07/30
0040ª@ óM XV 8/13
@ñ¹çê½âèÌðÅ·
ukasamav
07/30
2304ª@ óM XV 8/13
OñÌðÉêù³ð³êܵ½BºLÉÜÆßÄ èÜ·B
ukasamav
08/03 2236ª@ óM XV 8/13
OñÌù³àeÆ¡ÌÊðÅ·
NO4uæÓ©µÌÂ碨¶³ñv8/12 0533ª óM XV 8/13
¡ñÌâèÌqgÍAuoèÍAZZåwi¶njÌßâüèvŵ½B
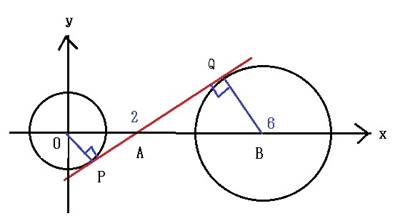
(1)
![]()
±Ìæ¤ÉÏ`·éÆA±Ì®Í2_![]() ðÔ¼üÌX«Å·B
ðÔ¼üÌX«Å·B
_![]() Æ_
Æ_![]() ÆÍA´_ÎÌÌÖWÉ èÜ·B
ÆÍA´_ÎÌÌÖWÉ èÜ·B
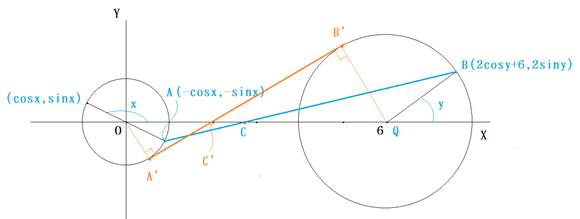
±Ì¼üÌX«ÌÅåÍA}ÌÔÌêÅ·B
¢OAfCeä¢QBfCfÅAÌäÍA1F2Å·B
æÁÄA_CfÌÀWÍ2Å·B
_![]() ðÊèAX«Ì¼üÍA
ðÊèAX«Ì¼üÍA![]()
±Ì¼üÆ´_ÆÌ£Í1ÈÌÅA
![]()
![]()
æÁÄAÅålÍA![]() Å·B
Å·B
(2)
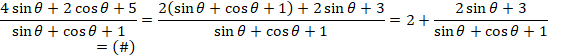
±±ÅAªêðÏ`µÜ·B
![]()
³çÉAªêðÝÄAªqðÏ`µÜ·B
![]()
![]()
æÁÄA()ÍA
![]()
![]()
![]()
±±ÅA
F̪ÍA´_Sża![]() Ì~üãÌ_aÆ_
Ì~üãÌ_aÆ_![]() ðÔ¼üÌX«Å·B
ðÔ¼üÌX«Å·B
ƪA![]()
ÌÍÍÅl¦êÎ梱ÆÉÈèÜ·B
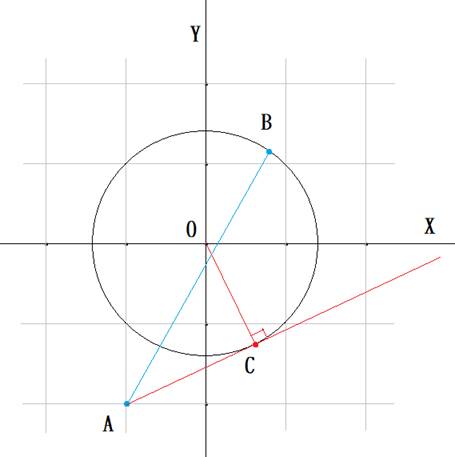
±Ì¼üÌX«ÌŬÍA}ÌÔÌêÅ·B
_![]() ðÊèAX«Ì¼üÍA
ðÊèAX«Ì¼üÍA![]()
±Ì¼üÆ´_ÆÌ£Í![]() ÈÌÅA
ÈÌÅA
![]()
![]()
æÁÄA(##)ÍA
![]()
æÁÄAŬlÍA![]() Å·B
Å·B
ÇÁâè1
_Bª´_A_Cª²Éæéæ¤É}ðzuµÜ·B
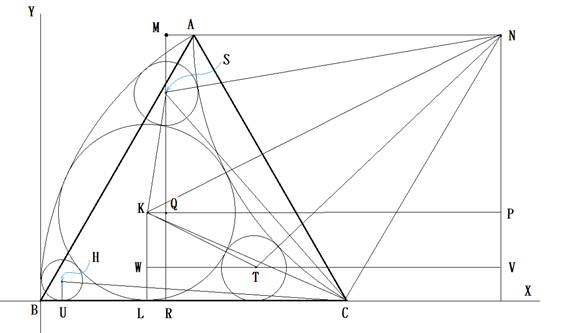
e~̼aÆSÌÀWðÌæ¤ÉµÜ·B
bFÆ![]() A³FÆ
A³FÆ![]() A¸FÆ
A¸FÆ![]() AFÆ
AFÆ![]()
~b̼aðßÜ·B
¼pOp`CKLæèA
![]()
¼pOp`KNPæèA
![]()
(1)A(2)æèA
![]()
±êð(1)ÉüêéÆA
![]()
![]() (0æè)
(0æè)
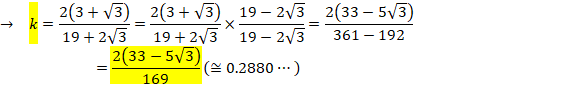
±êðÌ®ÉüêéÆA
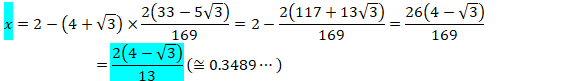
~³Ì¼aðßÜ·B
¼pOp`NSMæèA
![]()
¼pOp`CSRæèA
![]()
WJµÄAi3j©çi4jðøÆA
![]()
±êð(3)ÉüêÄAÅ®·éÆA
![]()
±±ÅAÌ]¿ðµÜ·B
}©çÍ0.1öxÈÌÅAµÉ ![]() ðãüµÄÝéÆA
ðãüµÄÝéÆA
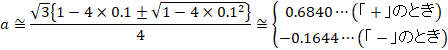
ͳÈÌÅAu+vÌêðp¢Ü·B
![]()
±êð(5)ÉüêÄ®·éÆA
![]()
¼pOp`SKQæèA
![]()
![]()
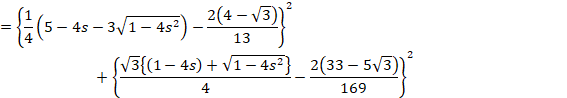
vZ·éÆA¤êµ¢±ÆÉA![]() ÌWª0ÉÈèÜ·B
ÌWª0ÉÈèÜ·B
![]()
2æµÄA®·éÆA
![]()
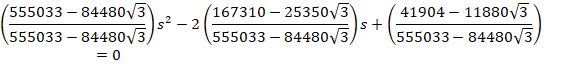
ªêðL»·éÆA
![]()
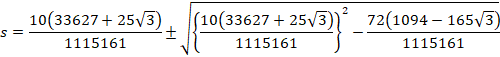
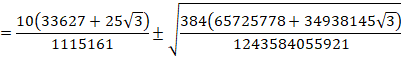
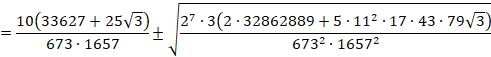
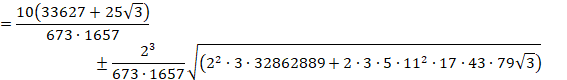
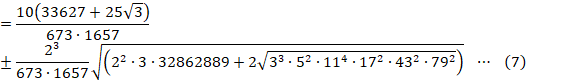
±êð![]() Ì`ɵ½¢ÌÅA
Ì`ɵ½¢ÌÅA
![]()
±êðð¢ÄA(½ÎÅ௶ŷ)
![]()
ä¦ÉA(7)ÍA
![]()
![]()
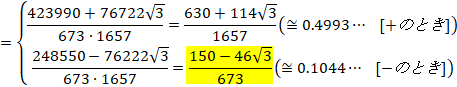
æÁÄA
![]()
Å·B
~¸Ì¼aðßÜ·B
¼pOp`CHUæèA
![]()
![]() ÈÌÅãÌ®Éãü·éÆA
ÈÌÅãÌ®Éãü·éÆA
![]()
![]()
±êÉA![]() A
A![]() ðüêÄA®·éÆA
ðüêÄA®·éÆA
![]()
![]() É¢ÄðÆA
É¢ÄðÆA
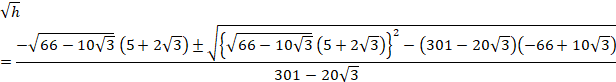
![]() æèA
æèA
![]()
![]()
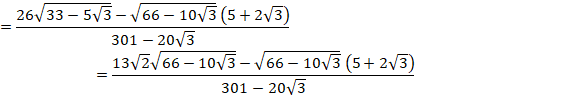
![]()
2æµÄA
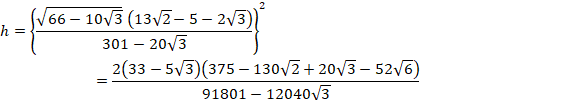
![]()
![]()
![]()
~̼aðßÜ·B
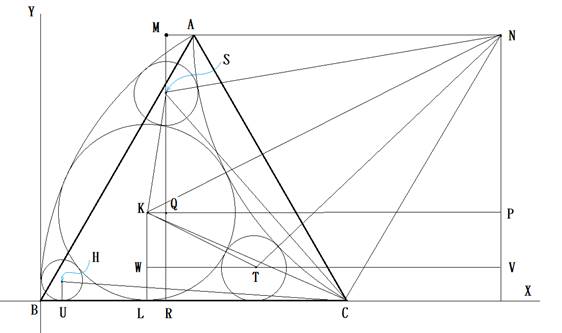
¼pOp`TNVæèA
![]()
¼pOp`TKWæèA
![]()
(8)Æ(9)æèA
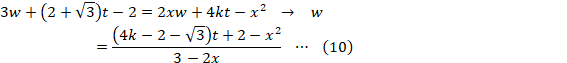
(10)ÉAÆðãüµÄA®·éÆA
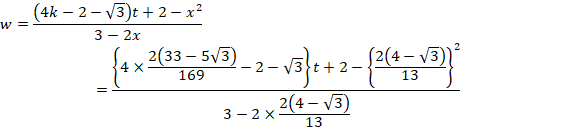
![]()
±êð(8)Éãü·éÆA
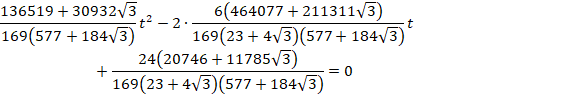
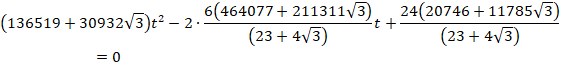
±êððÆA
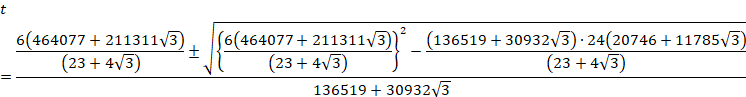
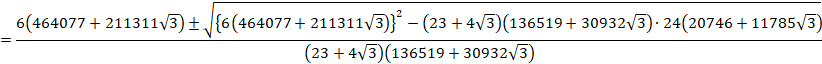
![]()
2dªÌªð![]() Ì`ɵ½¢ÌÅA
Ì`ɵ½¢ÌÅA
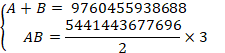
±êðð¢ÄA(½ÎÅ௶ŷ)
![]()
ä¦ÉA
![]()
æÁÄA
![]()
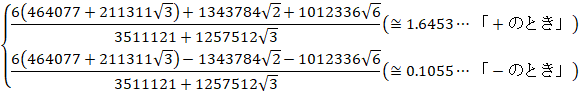
æÁÄ}CiXÌÆ«ð¿¢Ü·B
æÁÄ~̼aÍA
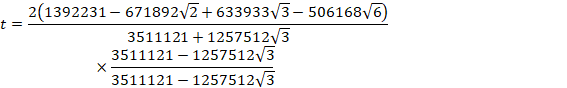
![]()
ÇÁâè2
AªÂêÍA(1ñÚE6ñÚ)A(7ñÚE12ñÚ)A¥¥¥A(1+6(|1)ñÚE6+6(|1)ñÚ)A¥¥¥
aªÂêÍA(2ñÚE5ñÚ)A(8ñÚE11ñÚ)A¥¥¥A(2+6(|1)ñÚE5+6(|1)ñÚ)A¥¥¥
bªÂêÍA(3ñÚE4ñÚ)A(9ñÚE10ñÚ)A¥¥¥A(3+6(|1)ñÚE4+6(|1)ñÚ)A¥¥¥
ÉN±èÜ·B
»ê¼êÌm¦ðvµÄ¢ÆA
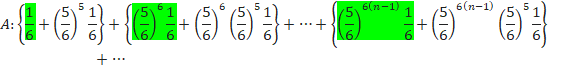
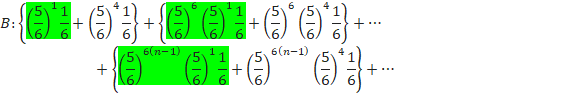
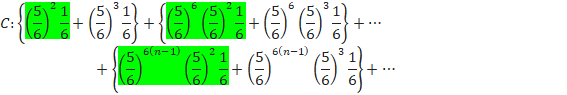
»ê¼êÌm¦ðO¼Æã¼Éª¯Ä«µÄ¢«Ü·B
O¼Æã¼Éª¯éÆA»ê¼ê³ÀäÌaÉÈèÜ·B
`ÌÂm¦ÍA
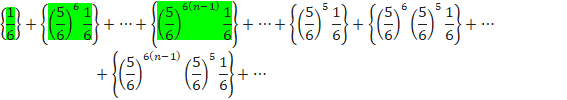
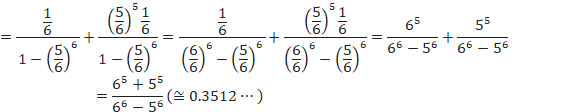
BÌÂm¦ÍA
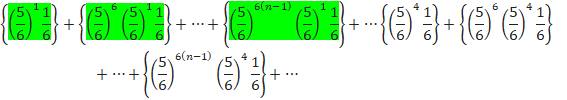
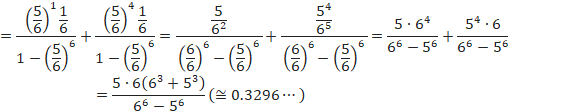
CÌÂm¦ÍA
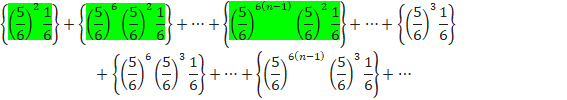
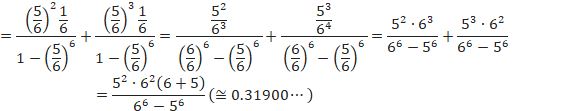
O̽ßÉm¦ðv·éÆA
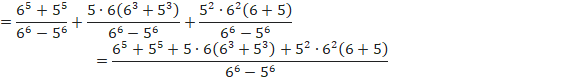
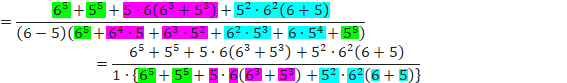
![]()
u
̬êv @@@@@@@@@@@@@@@@@ XV 8/13
ð