令和８年２月１日

[流れ星]

　　第463回数学的な連続応募解答

　　　＜解答募集期間：１月４日〜２月１日＞

［2026の雑題］
問題１　

（１）ｘ^８−ｘ＋１　を因数分解せよ。

（２）2026⁸−2025は素数か合成数か判定せよ。

ヒント　−１の3乗根

問題２　ｘ^２＋２ｘ＋４＝０の解をα,βとするとき,

（１）α^ｎ＋β^ｎをｎで表せ。ただし,ｎは自然数

（２）｜α²⁰²⁶＋β²⁰²⁶｜を31で割った余りを求めよ。

ヒント　８の3乗根

問題３（１）2026を自然数の3乗和で表し,その個数を6個以内でできるだけ見つけてください。

（２）（１）で見つけたなかで、2026²⁰²⁶をできるだけ少ない個数の自然数の３乗和でひとつ表せ。

追加問題（出題者は「ジョーカー」）　新作シリーズ

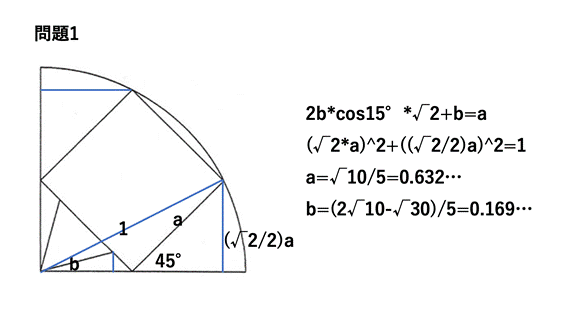
四分円内の正方形と正三角形の1辺について『３』　

問題１　　シリーズ5問目

正方形と正三角形の1辺が異なる（ａ＞ｂ),

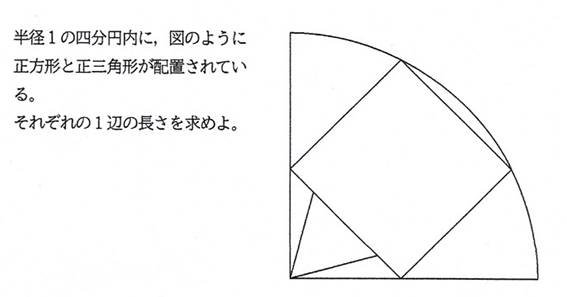
問題２　シリーズ6問目

正方形と正三角形の1辺が異なる（ａ＞ｂ),

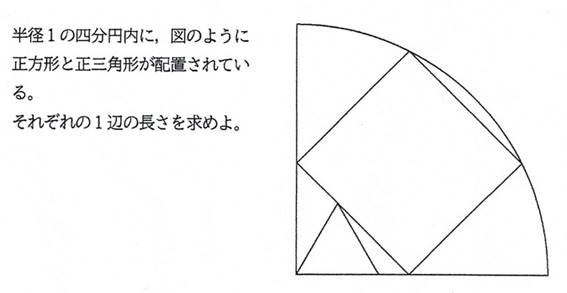
NO1「ジョーカー」 　 1/04　　 17時17分 　 受信 更新 ２/１

寄せられた解答です

NO2「よふかしのつらいおじさん」1/05 15時53分受信 更新 2/1

　寄せられた解答です

NO3「スモークマン」 1/11 　15時01分　　　　受信 更新 2/1

新年明けましておめでとうございます。

今年もよろしくお願いいたします。

今年初挑戦！！

問題１

（１） ｘ８−ｘ＋１を因数分解せよ。

x^3=-1

(x+1)(x^2-x+1)=0 の解は-ω

(-ω)^3=^1

(-ω)^8-(-ω)+1=ω^2+ω+1=0

So…

x^8-x+1=(x^2-x+1)(x^6+x^5-x^3-x^2+1)

（２）20268−2025は素数か合成数か判定せよ。

2026=x

x^8-x+1となるから、(1)より合成数

∵2026^2-2026+1=4102651≠1

問題２ ｘ^２＋２ｘ＋４＝０の解をα,βとするとき,

（１） α^ｎ＋β^ｎをｎで表せ。

(x-2)(x^2+2x+4)=x^3-8=0

So…

α=2ω,β=2ω^2

・n=3k のとき

2^n+2^n=2^(n+1)

・n=3k+1 のとき

2^(n-1)*2ω+2^(n-1)*2ω^2=-2^n

・n=3k+2 のとき

2^(n-2)*4ω^2+2^(n-2)*4ω=-2^n

（２）｜α^2026＋β^2026｜を31で割った余りを求めよ。

ヒント ８の3乗根

2026≡1. (mod 3)

So…|α^2026+β^2026|=2^2026

2^5=32≡1 (mod 31)

So…

2^2026≡2 (mod 31)

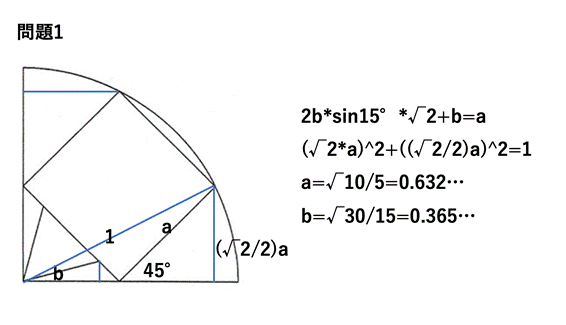
<水に流れ：ｂの値が間違っています＞

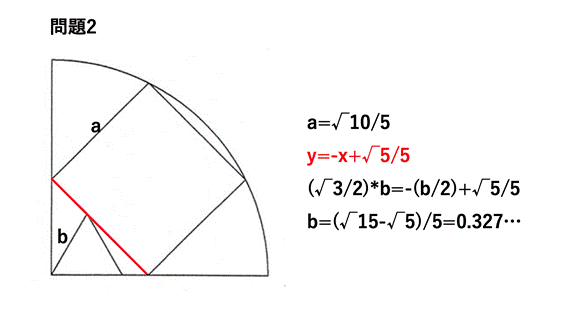
問題３

（１）2026を自然数の3乗和で表し,その個数を6個以内でできるだけ見つけてください。(AIに教えてもらった...^^;v)

11^3+7^3+7^3+2^3+1^3

12^3+6^3+3^3+3^3+3^3+1^3

11^3+7^3+6^3+4^3+4^3+2^3

10^3+9^3+6^3+3^3+3^3+3^3

(２）（１）で見つけたなかで、20262026をできるだけ少ない個数の自然数の３乗和でひとつ表せ。

補足（１）は数学ソフトで見つけても可

(1) から、5項の和が一番少ない。

So…

2026^2026

=2026^2025*2026

=(2026^675)^3*(11^3+7^3+2^3+1^3)

=(11*2026^675)^3+(7*2026^675)^3+(7*2026^675)^3+(2*2026^675)^3+(2026^675)^3

NO4「kasama」 　　　　　　　1/20 　00時59分　 　　受信 更新 2/1

寄せられた解答です

NO5「三角定規」 1/30 13時31分　 受信 更新 2/1

寄せられた解答です

水の流れ　

問題１の（１）答　　　　　　　　　　　　　　　　　　　　　更新　２/1

高次方程式の因数分解のとき,多くはｘ^２＋ｘ＋１，またはｘ^２―ｘ＋１を因数に持つ場合が多いと経験している。

そこで,±１の3乗根の虚数解を±ω,±ω^２とくと, ω^２＋ω＋１＝０

または, ω^２―ω＋１＝０である。

ここで,x=ωをｘ^８−ｘ＋１代入すると,ω^８―ω＋１＝ω^２―ω＋１となり０ではない。ｘ^８−ｘ＋１＝０は　x=ωを解に持たない。

次に,ｘ＝―ωを代入すると, ω^８＋ω＋１＝ω^２＋ω＋１＝０となる。

したがって,ｘ＝―ωを解にもつ。即ち,与式はｘ^２―ｘ＋１を因数に持つ。

　よって, ｘ^８−ｘ＋１をｘ^２―ｘ＋１で割ると,商はｘの6次式

ｘ^８−ｘ＋１＝(ｘ^２―ｘ＋１)(ｘ^６＋ｘ^５−ｘ^３−ｘ^２＋１)　・・・答

注：ｘ^６＋ｘ^５−ｘ^３−ｘ^２＋１が規約多項式であることを示さねばならないが。

問題１の（２）答　

　ｘ＝2026とくと,（１）から

ｘ^８−ｘ＋１＝2026^８−2025＝(2026^２―2025)(大きな数)

　積の形にできたから, 2026⁸−2025は合成数である。・・・答

参考に, 2026⁸−2025＝4,102,651＝7・19・109・283と素因数分解できる。

補追　問題３（１）で6個の３乗和の場合は時間がなくて発見できていませんでした。