令和６年６月２３日

[流れ星]

　　第442回数学的な連続応募解答

　　　＜解答募集期間：5月26日〜6月23日＞

「雑題3問］

お詫びして訂正いたします。5月26日午後11時記

追加問題（出題者は「ジョーカー」）

新シリーズ（正三角形の辺や円弧によって囲まれる図形内の3円の半径について）４・５問目

問題1

　

問題２

NO1「ジョーカー」 　　 5/27 　01時28分 受信 更新 6/23

寄せられた解答です

NO2「スモークマン」 5/28 20時05分　 　受信 更新 6/23

雑題3題

(1)

6x^2<27x

x=1〜4

・x=1 のとき

2(y+z+yz)=9(1+y+z)

2yz=9+7(y+z)

y(2z-7)-(7/2)(2z-7)=9+49/2=67/2

(2y-7)(2z-7)=67

2y-7=1, 2z-7=67・・・y=4,z=37

・x=2 のとき

2(2y+2z+yz)=9(2+y+z)

2yz=18+5(y+z)

y(2z-5)-(5/2)(2z-5)=18+25/2=61/2

(2y-5)(2z-5)=61

2y-5=1,2z-5=61・・・y=3,z=33

・x=3のとき

2(3y+3z+yz)=9(3+y+z)

2yz=27+3(y+z)

y(2z-3)-(3/2)(2z-3)=27+9/2=63/2

(2y-3)(2z-3)=63=1*63=3*21=7*9

y=2,z=33・・・y=2<x=3 でなし

y=3,z=12

y=5,z=6

・x=4 のとき

2(4y+4z+yz)=9(4+y+z)

2yz=36+y+z

y(2z-1)-(1/2)(2z-1)=36+1/2=73/2

(2y-1)(2z-1)=73=1*73・・・y=1<x=4 でなし

結局…

(x,y,z)=(1,4,37), (2,3,33), (3,3,12), (3,5,6) 正解

(2)

m^3+n^3-9mn=p-27

m^3+n^3+3^3-3(3*m*n)

=(m+n+3)(m^2+n^2+3^2-mn-3m-3n)

So…

m^2+n^2+3^2-mn-3m-3n

=(1/2){(m-n)^2+(m-3)^2+(n-3)^2}

=1

So…

m=3,n=4 or n=3,m=4 or n=m=4

m+n+3が素数になるのは、n=m=4 のとき、p=11 だけ

つまり、

(m,n,p)=(4,4,11)　正解

筑波大学２０２２年問題の解答

m^3+n^3-6mn=p-8 なら

(m+n+2)(1/2){(m-n)^2+(m-2)^2+(n-2)^2}=p

So…

m=2,n=3 or n=2,m=3,or m=n=3

このとき、m+n+2が素数は前２者

(m,n,p)=(2,3,7),(3,2,7)　正解

(3)

(1+x)(1+y)(x+y)

=(1+(x+y)+xy)(x+y)=300

=300

x^3+y^3

=(x+y)^3-3(x+y)xy

=99

x+y=u

xy=v

3u^2+3u*v+3u=900

u^3-3u*v=99

u^3+3u^2+3u=999

(u+1)^3=10^3

u+1=10,10ω,10ω^2

so…

u=x+y=9, 10ω-1, 10ω^2-1 正解

NO3「kasama」 6/03 23時47分　　 受信 更新 6/23

寄せられた解答です

NO4「よふかしのつらいおじさん」 6/08 　17時48分 受信　更新6/23

寄せられた解答とコメントです。

問題1は、なかなかすっきりしなかったのですが、

X^2≦yzの式を考えて、すっきりしました。

問題2は場合分けで、迷路に入っていましたが、

HPで問題が訂正されているのをみて、すぐに式の変形を思いつきました。

追加問題1は、AKの表し方で計算の手間に差が出るようです。

はじめ、ｋの4次方程式が出てくるような方法でしたが、

解答の方法で2次方程式になりました。しかし、この解答は面倒でした。

（解けませんでしたが、4次方程式を見ていて、甲と乙の半径が等しいと気づきました）

問題2はやり方を変えました。（ｓとおいて三角関数で表す）

ｓとおくやり方では、面倒な2重根号を外す場面はないと思います。

＜水の流れ：コメントありがとうございます＞

NO5「二度漬け白菜」 6/13 21時09分　 受信 更新 6/23

第442回数学的な応募問題 「雑題3問」の解答：

[問題1]

(x,y,z)=(1,4,37),(2,3,33),(3,3,12),(3,5,6)(答) 

0＜x≦y≦zより，x*x≦y*z.

よって，

2*(x*y+y*z+z*x)

≧2*(x*y+x*x+z*x)

=2*x*(x+y+z).

2*(x*y+y*z+z*x)=9*(x+y+z)とから，

2*x*(x+y+z)≦9*(x+y+z)

→2*x≦9.

よって，x=1 or 2 or 3 or 4.

与式：2*(x*y+y*z+z*x)=9*(x+y+z)は次のように変形できる．

(2*y+(2*x-9))*(2*z+(2*x-9))=4*x^2-18*x+81.

・x=1の場合：

(2*y-7)*(2*z-7)=67 

→(2*y-7,2*z-7)=(1,67) (∵ 2*z-7≧2*y-7≧2*x-7=-5.)

→(y,z)=(4,37).

・x=2の場合：

(2*y-5)*(2*z-5)=61

→(2*y-5,2*z-5)=(1,61) (∵ 2*z-5≧2*y-5≧2*x-5=-1.)

→(y,z)=(3,33).

・x=3の場合：

(2*y-3)*(2*z-3)=63

→(2*y-3,2*z-3)=(3,21)or(7,9) (∵ 2*z-3≧2*y-3≧2*x-3=3.)

→(y,z)=(3,12)or(5,6).

・x=4の場合：

(2*y-1)*(2*z-1)=73

→y,zは存在しない． (∵ 2*z-1≧2*y-1≧2*x-1=7.)

[問題2]

(m,n,p)=(2,2,7),(4,4,11) (答)

与式は次のように変形できる．

p=(m+n+3)*(m^2-(n+3)*m+n^2-3*n+9).

与えられた条件を満たすためには，

(m+n+3)=p かつ

(m^2-(n+3)*m+n^2-3*n+9)=1 

であることが必要．

後者はmについての2次方程式であり，判別式は

0以上であることが必要．よって，

(n+3)^2-4*(n^2-3*n+8)≧0.

つまり，4≧3*(n-3)^2.

よって，n=2 or 3 or 4.

[問題3]

x+y=9 または -6+i*5*3^(1/2) または -6-i*5*3^(1/2) (答) 

x+y=k とおく．

99

=x^3+y^3

=(x+y)^3-3*x*y*(x+y)

=k^3-3*k*x*y.

よって，

x*y=(k^3-99)/(3*k).

これを(1+x)*(1+y)*(x+y)=300に代入する．

(1+x)*(1+y)*(x+y)=300

→(1+x+y+x*y)*k=300

→(1+k+(k^3-99)/(3*k))*k=300

→k+k^2+k^3/3-33=300

→k^3+3*k^2+3*k=999

→k^3+3*k^2+3*k+1=1000

→(k+1)^3=10^3

→k+1=10 or 10*ω or 10*ω^2.

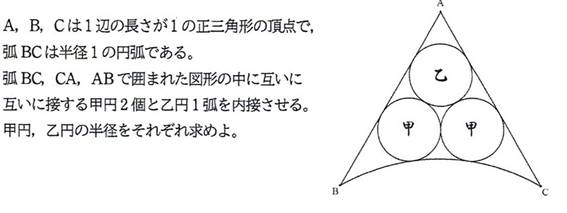
[追加問題 1]

甲円の半径は，3*6^(1/2)+4*3^(1/2)-5*2^(1/2)-7

乙円の半径は，3*6^(1/2)+4*3^(1/2)-5*2^(1/2)-7 (答)

甲円の半径をr，乙円の半径をRとする．

xy直交座標上を設定して考える．

A(0,0),

B((1/2)*3^(1/2),-1/2),

C((1/2)*3^(1/2),1/2)

となるようにする．

その中心が点Cに最も近い甲円の中心をD，

乙円の中心をEとする．

AE=2*Rであるから，E(2*R,0).

Dは直線：y=tan(15°)*x上にあり，そのy座標はrであるから，

Dの座標は，D(r/tan(15°),r)．

甲円は，点Aを中心とする半径1の円:x^2+y^2=1に内接する．

この二つの円の中心の位置関係より，DA=1-r.

DA=r/sin(15°)であることとから，

r/sin(15°)=1-r ---(1)

さらに，DE=r+Rであるから，

(r/tan(15°)-2*R)^2+(r-0)^2=(r+R)^2 ---(2)

(1),(2)より，

r=R=3*6^(1/2)+4*3^(1/2)-5*2^(1/2)-7.

[追加問題 2]

甲円の半径は，4+6^(1/2)-2*(3^(1/2)+2^(1/2))，

乙円の半径は，4+6^(1/2)-2*(3^(1/2)+2^(1/2)) (答)

甲円の半径をr，乙円の半径をRとする．

xy直交座標上を設定して考える．

頂点A,B,Cの座標が，それぞれ，

A(0,0),

B((1/2)*3^(1/2),-1/2),

C((1/2)*3^(1/2),1/2)

となるようにする．

その中心が点Cに最も近い甲円の中心をD，

乙円の中心をEとする．

AE=2*Rであるから，E(2*R,0).

Dは直線：y=tan(15°)*x 上にあり，そのy座標はrであるから，

Dの座標は，D(r/tan(15°),r)．

甲円は，点G(3^(1/2),0)を中心とする半径1の円:(x-3^(1/2))^2+y^2=1

に外接するから，DG=1+r であり，

(r/tan(15°)-3^(1/2))^2+(r-0)^2=(1+r)^2 ---(1)

さらに，DE=r+Rであるから，

(r/tan(15°)-2*R)^2+(r-0)^2=(r+R)^2 ---(2)

(1),(2)より，

r=R=4+6^(1/2)-2*(3^(1/2)+2^(1/2)).

第24回数学的な応募問題 ［緊急連絡網］ 問題3 の解答：

すでに頂いた応募解答です。

実際には S(n)=(2*n-4) であることが知られています．

S(n)≦(2*n-4)であることは次のように示せます．

(証明)

n人のうちの特定の4人を A,B,C,D とし，それ以外の(n-4)人を，

P[1],P[2],…,P[n-4] とする．

AとP[1]の二人が通話することを (A-P[1]) というように書き表すことにする．

n人のそれぞれが持つ独自の情報を，n人すべてで共有するためには，以下に示す

ように高々(2*n-4)回の通話で十分である．

(A-P[1])

(A-P[2])

(A-P[3])

……

(A-P[n-4])

(A-B)

(C-D)

(B-C)

(A-D)

(A-P[1])

(A-P[2])

(A-P[3])

……

(A-P[n-4])

つまり，まずAがP[1],P[2],…,P[n-4]と通話し，その後，A,B,C,Dの4人の間で

通話を行う．さらにその後，Aが再びP[1],P[2],…,P[n-4]と通話する．

これにより，S(n)≦(2*n-4) が示せた．(証明終)

さらに S(n)=(2*n-4) を示すためには，S(n)≧(2*n-4)を示せばよいわけですが，

これの証明は以下の論文にあります．

『Gossips and telephones』

https://www.sciencedirect.com/science/article/pii/0012365X72900015

日本語による証明もあります．

以下の本に「ゴシップ問題」と題して，S(n)=(2*n-4) であることの証明

が載っています．

『離散数学入門』 秋山仁・R.L.Graham 著 朝倉書店

(以上)

N6「三角定規」 6/22 00時03分　 受信 更新 6/23

寄せられた解答です

＜コメント＞

[問題１] は対称性を利用したもっとスマートな解があると思うのですが…私には…

[追加問題] 初め甲乙の半径が等しいことに気づかず，乙の計算に結構手間を掛けたのですが，

結果が等しかったことから，まず等しいことを示す解に書き改めました。

追加問題[2], 二重根号が外れることに気がつきませんでした。

計算は Wolfram に任せきりでしたので !!

「水の流れ」 　　　　　　　　　　　　　　 更新 6/23

皆さん、問題や質問に答えてください。一部でも構いませんから, 解答とペンネームを添えて, メールで送ってください。待っています。