令和６年７月２１日

[流れ星]

　　第443回数学的な連続応募解答

　　　＜解答募集期間：6月23日〜7月21日＞

「cosθのｎ倍角］

追加問題（出題者は「ジョーカー」）

新シリーズ（正三角形の辺や円弧によって囲まれる図形内の3円の半径について）６・７問目

問題1

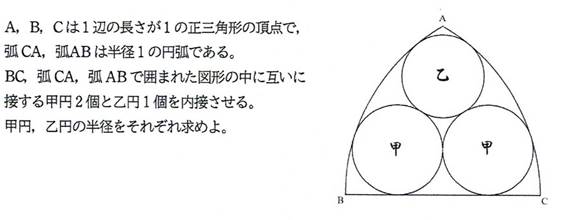
問題２

　

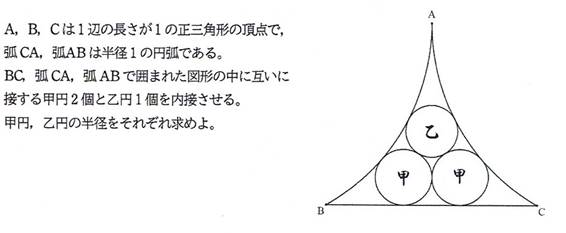
NO1「ジョーカー」 　 6/23 　21時28分 受信 更新 7/21

寄せられた解答です

NO2「スモークマン」 6/27 16時27分　 受信 更新 7/21

今回もできたと思うものだけの投稿です Orz

問題 cosθのn倍角

(2)

θ=((2k-1)*π/10) は、k=1〜5において、cos(5θ)=0

so…

16x^5-20x^3+5x=0 の根

ここで、cos(5π/10)=0 なので

x(16x^4-20x^2+5)=0 から、

残りの根が

16x^4-20x^2+5=0 の根

So…

与式=5/16

(4)

同様に、

θ=(2k-1)π/14 はcos(7θ)=0

so…

64ｘ6−112ｘ4＋56ｘ2−7=0 の根

So…

与式=-7/64

(5)

(-1)^n*(2n+1)/2^(2n)

「スモークマン」 6/27 23時40分　 受信 更新 7/21

追加問題１

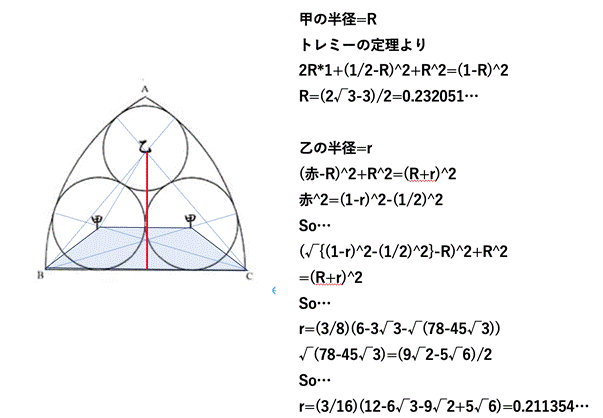
＜「スモークマン」からの問題提起＞

ちなみに、「ヤドカリの気ままな数学」というサイトにも参加してますが、ここにも強者が多くいらっしゃいます。

今、https://okayadokary.blog.fc2.com/blog-entry-5022.html　の問題1904

「　Aさん，Bさん，Cさんは共に 1から339までの番号が１つずつ書かれた339枚の番号札を持っていて、その中から、Aさんは２枚，Bさんは３枚，Cさんは１枚を無作為に取り出します。

　Aさんの取り出す最小の番号を a ，Bさんの取り出す最大の番号を b ，Cさんの取り出す番号を c として、

　a≧b である確率は？

　また、a≧b であるとき a≧c≧b である条件付確率は？」

を考えていますがなかなか...いい手を思いつけないでいます...^^;;

N3「二度漬け白菜」 6/29 11時23分　 受信 更新 7/21

第443回の応募問題 を考えました．

よろしくお願いします．

まず，次の等式 (☆) が成り立つことを証明しておきます．

以下では，Iは虚数単位(I^2=-1)を表しています．

任意の正整数 n に対して，次の等式が成り立つ．

Π[k=0〜2*n,k≠n]cos(π*(2*k+1)/(4*n+2))=(2*n+1)*(-1/4)^n ---(☆)

(証明)

Π[k=0〜2*n,k≠n]cos(π*(2*k+1)/(4*n+2))

=Π[k=0〜n-1]cos(π*(2*k+1)/(4*n+2))*cos(π-π*(2*k+1)/(4*n+2))

=(-1)^n*Π[k=0〜n-1](cos(π*(2*k+1)/(4*n+2)))^2

=(-1)^n*Π[r=1〜n](cos(π*(2*(n-r)+1)/(4*n+2)))^2

=(-1)^n*Π[r=1〜n]cos(π/2-r*π/(2*n+1)))^2

=(-1)^n*Π[r=1〜n](sin(π*r/(2*n+1)))^2

=(-1)^n*Π[r=1〜n]sin(π*r/(2*n+1))*sin(π*r/(2*n+1))

=(-1)^n*Π[r=1〜n]sin(π*r/(2*n+1))*sin(π-π*r/(2*n+1))

=(-1)^n*Π[r=1〜n]sin(π*r/(2*n+1))*sin(π*(2*n+1-r)/(2*n+1))

=(-1)^n*Π[r=1〜2*n]sin(π*r/(2*n+1))

=(-1)^n*Π[r=1〜2*n](1/(2*I))*(exp(I*π*r/(2*n+1))-exp(-I*π*r/(2*n+1)))

=(-1)^n*(1/(2*I))^(2*n)*Π[r=1〜2*n](-exp(-I*π*r/(2*n+1)))*(1-exp(2*I*π*r/(2*n+1)))

=(-1)^n*(1/(2*I))^(2*n)*(-1)^(2*n)*exp((-I*π/(2*n+1))*(1+2+…+2*n))*Π[r=1〜2*n](1-exp(2*I*π*r/(2*n+1)))

=(1/2)^(2*n)*exp(I*(-n*π))*Π[r=1〜2*n](1-exp(2*I*π*r/(2*n+1)))

=(1/4)^n*cos(-n*π)*(2*n+1) ---(★)

=(2*n+1)*(-1/4)^n　(証明終)

(★)について：

exp(2*I*π*r/(2*n+1)) r=1,2,…,2*n は方程式

x^(2*n+1)-1=(x-1)*(x^(2*n)+x^(2*n-1)+…+x^2+x+1)=0 

の相異なる2*n個の虚根である．

よって，x^(2*n)+x^(2*n-1)+…+x^2+x+1は次のように因数分解できる．

x^(2*n)+x^(2*n-1)+…+x^2+x+1=Π[r=1〜2*n](x-exp(2*I*π*r/(2*n+1)))．

x=1を代入して，(2*n+1)=Π[r=1〜2*n](1-exp(2*I*π*r/(2*n+1))).

「cosθのn倍角］の解答：

(1)f(x)=16*x^5-20*x^3+5*x (答)

(2)(与式) = 5/16 (答)

(3)f(x)=64*x^7-112*x^5+56*x^3-7*x (答)

(4)(与式) = -7/64 (答) 

(5)Π[k=0〜2*n,k≠n]cos(π*(2*k+1)/(4*n+2))=(2*n+1)*(-1/4)^n (答)

チェビシェフの多項式について：

cos(n*θ)をcos(θ)の多項式で表すと次のようになります．

cos(n*θ) = Σ[k=0〜floor(n/2)](-1)^k*(n/(n-k))*binomial(n-k,k)*2^(n-1-2*k)*(cos(θ))^(n-2*k) ---(☆☆)

たとえば，cos(123*θ)をcos(θ)の多項式で表したときの，(cos(θ))^45 の係数は，

(n=123,k=39を代入して，)

(-1)^39*(123/(123-39))*binomial(123-39,39)*2^(123-1-2*39)

=-34989091723911923921720529310848122880.

(☆☆)は次のようにすれば得られます．

A,Bを文字変数とします．

A^n＋B^nを基本対称式 A+B,A*B で表すと次のようになります．

A^n＋B^n = Σ[k=0〜floor(n/2)](n/(n-k))*binomial(n-k,k)*(A+B)^(n-2*k)*(-A*B)^k.

(これは，等式 -log(1-A*t)-log(1-B*t)=-log(1-((A+B)*t-A*B*t^2)) の両辺をマクローリン展開し，

両辺のt^nの係数を比較することにより得られます．)

よって，

(A^n＋B^n)/2 = Σ[k=0〜floor(n/2)](n/(n-k))*binomial(n-k,k)*2^(n-1-2*k)*((A+B)/2)^(n-2*k)*(-A*B)^k.

ここで，A=exp(I*θ),B=exp(-I*θ) を代入して，

cos(n*θ) = Σ[k=0〜floor(n/2)](-1)^k*(n/(n-k))*binomial(n-k,k)*2^(n-1-2*k)*(cos(θ))^(n-2*k)

となり，(☆☆)が得られました．

[追加問題 1]

甲円の半径は，3^(1/2)-3/2,

乙円の半径は，(1/16)*(36+15*6^(1/2)-18*3^(1/2)-27*2^(1/2)) (答)

甲円の半径をr，乙円の半径をsとする．

xy直交座標上を設定して考える．

A(0,3^(1/2)),

B(-1/2,0),

C(1/2,0)

となるように座標を設定する．

その中心が点Cに近い方の甲円の中心をD，

乙円の中心をEとする．

Dの座標は，D(r,r) である．

Eの座標を，E(0,t) とおく．

(DB)^2=(1-r)^2 であるから，

(r+1/2)^2+r^2=(1-r)^2 ---(1)

(EB)^2=(1-s)^2 であるから，

(1/2)^2+t^2=(1-s)^2  ---(2)

(DE)^2=(r+s)^2 であるから，

r^2+(r-t)^2=(r+s)^2  ---(3)

(1),(2),(3)を解いて，

r=3^(1/2)-3/2,

s=(1/16)*(36+15*6^(1/2)-18*3^(1/2)-27*2^(1/2)),

t=(1/16)*(22*3^(1/2)+21*2^(1/2)-9*6^(1/2)-36)

を得る．

[追加問題 2]

甲円の半径は，1-(1/2)*3^(1/2),

乙円の半径は，(1/23)*(4*6^(1/2)+20*3^(1/2)-28*2^(1/2)-2) (答)

甲円の半径をr，乙円の半径をsとする．

xy直交座標上を設定して考える．

A(0,3^(1/2)),

B(-1/2,0),

C(1/2,0)

となるように座標を設定する．

その中心が点Cに近い方の甲円の中心をD，

乙円の中心をEとする．

Dの座標は，D(r,r) である．

Eの座標を，E(0,t) とおく．

また，点(1,(1/2)*3^(1/2))をGとする．

(GD)^2=(1+r)^2 であるから，

(1-r)^2+(r-(1/2)*3^(1/2))^2=(1+r)^2 ---(1)

(GE)^2=(1+s)^2 であるから，

(1-0)^2+((1/2)*3^(1/2)-t)^2=(1+s)^2 ---(2)

(DE)^2=(r+s)^2 であるから，

r^2+(r-t)^2=(r+s)^2         ---(3)

(1),(2),(3)を解いて，

r=1-(1/2)*3^(1/2),

s=(1/23)*(4*6^(1/2)+20*3^(1/2)-28*2^(1/2)-2),

t=(1/46)*(8*6^(1/2)+36*2^(1/2)-29*3^(1/2)-4)

を得る．

(以上)

＜水の流れ：＞任意の正整数 n に対して，次の等式が成り立つ．

Π[k=0〜2*n,k≠n]cos(π*(2*k+1)/(4*n+2))=(2*n+1)*(-1/4)^n ---(☆)

一般から証明とは想定外でした。

　ご存知だったのですね。

チェビシェフの多項式について：言葉は知っていましたし、誰か考察の中できずいてもらえないかと　想定していました。深い考察に感謝します。＞

NO4「kasama」 7/01 23時57分　　 受信 更新 7/21

寄せられた解答です

「kasama」 7/06 17時37分　　 受信 更新 7/21

追記された解答です

NO5「よふかしのつらいおじさん」 7/10 21時48分 受信 更新 7/21

寄せられた解答です

NO6「三角定規」 7/14 21時25分　 受信 更新 7/21

寄せられた解答です

水の流れ　　　　　　　　　　　　　　　更新　　　　7月21日

問題はcosθのｎ倍角の奇数の場合です。

で、偶数の場合も含めて、書いておきます。

ただし、cosθ＝ｘとする。

ｆ(cosθ)＝ｘ　

ｆ(cos２θ)＝2ｘ^２−1　

ｆ(cos３θ)＝4ｘ^３−3ｘ　

ｆ(cos４θ)＝8ｘ^４−8ｘ^２＋1　　

ｆ(cos５θ)＝16ｘ^５−20ｘ^３＋5ｘ　

ｆ(cos６θ)＝32ｘ^６−48ｘ^４＋18ｘ^２−１　

ｆ(cos７θ)＝64ｘ^７−112ｘ^５＋56ｘ^３−7ｘ　

ｆ(cos８θ)＝128ｘ^８−256ｘ^６＋160ｘ^４−32ｘ^２＋１　

ｆ(cos９θ)＝256ｘ^９−576ｘ^７＋432ｘ^５−120ｘ^３＋９ｘ　

ｆ(cos10θ)＝512ｘ^１０−1280ｘ^８＋1120ｘ^６−400ｘ^４＋50ｘ^２−１

・・・

ｆ(cosｎθ)の式をチェビシェフ多項式といいます

参考に第7１回「余弦のｎ倍角」をご覧ください。

皆さん、問題や質問に答えてください。一部でも構いませんから, 解答とペンネームを添えて, メールで送ってください。待っています。