令和７年３月２日

[流れ星]

　　第451回数学的な連続応募解答

　　　＜解答募集期間：２月２日〜３月２日＞

［ガウス記号(3)］

　　

追加問題（出題者は「ジョーカー」）　新作シリーズ9,10問目

問題1

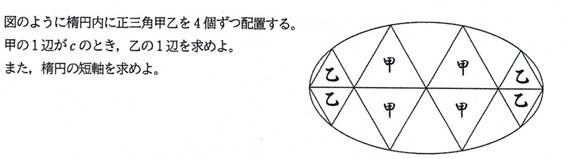
問題２

　

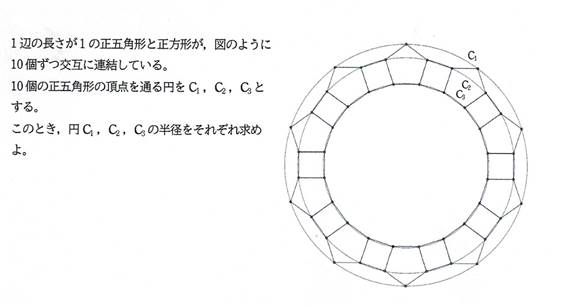
NO1「ジョーカー」 　 02/02 　　 17時19分 受信 更新 3/2

寄せられた解答です

NO2「よふかしのつらいおじさん」 2/8 16時56分 受信 更新 3/2

寄せられた解答です

NO3「スモークマン」 02/12 23時27分　 受信 更新 3/2

追加問題１

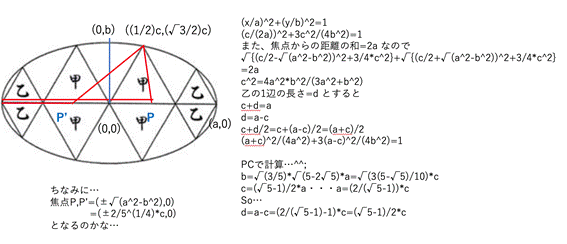
＜水の流れ：乙の1辺の長さ　 乙の1辺は、(√5-1)/2 cは正解です

短軸の長さは、 √(30(5-√5) )/5 cですが、時間があればと思います＞

追加問題２

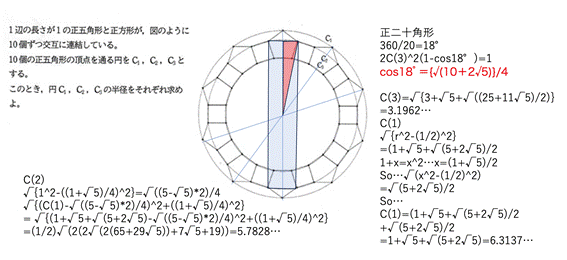
＜水の流れ：C3は√((3+√5)(4+√(10+2√5) ) )/2 (=3.196226⋯)＊＊＊正解

こちらの答えは　C1＝4.695717こちらの答えはC2=4.186838⋯

時間があれば再考下されば有難いです＞

「スモークマン」 02/14 20時50分　 受信 更新 3/2

設問1

2^2-1個の1

3^2-2^2個の2

…

45^2-44^2個の44

1個の45

Σ[k=1,44]((k+1)^2-k^2)k+45

=Σ(2k^2+k)+45

=2*44*45*89/6+44*45/2+45

=59775

設問2

2^3-1個の1

3^3-2^3個の2

…

n^3-(n-1)^3個の(n-1)

Σ[k=1,n-1]((k+1)^3-k^3)k

=(n-1)n^2(3n+1)/4

So…

(n-1)n^2(3n+1)/4+n

=n(n+1)(3n^2-5n+4)/4

設問3

Σ[k=1,2025]2^[k]=a*2^b+c

Σ[k=1,44]((k+1)^2-k^2)k

2^k*((k+1)^2-k^2)

=Σ[k=1,44]2^k*(2k+1)

S

=2*3+2^2*5+2^3*7+…+2^44*49+2^45

2S=2^2*3+2^3*5+2^4*7+…+2^44*47+2^45*49+2^46

2S-S=-6-2*(2^2+2^3+…+2^44)+48*2^45+2^46

S=48*2^45+2^46-8*(2^43-1)-6

=48*2^45+2

=6*2^48+2

＜水の流れ：2^44*49を2^44*89に修正すれば正当に至る＞

設問4

n=6m…[6m/2]+[6m/3]=5m・・・5m/6m=5/6

n=6m+1も同じ

n=6m+2…(5m+1)/6m

n=6m+3…(5m+2)/6m

n=6m+4…(5m+3)

n=6m+5…(5m+3)

結局…5/6

NO4「二度漬け白菜」 02/26 9時45分　 受信 更新 3/2

第451回の応募問題の解答：

[設問1](与式) = 59775 (答)

[設問2](与式) = n*(n+1)*(3*n^2-5*n+4)/4 (答)

正整数 n, r に対して，

a(n,r)=Σ[k=1〜n^r]floor(k^(1/r))

とする．

floor(k^(1/r))=m ⇔ m^r≦k<(m+1)^r であるから，

a(n,r)

=Σ[k=1〜n^r]floor(k^(1/r))

=Σ[k=0〜n^r]floor(k^(1/r))

=Σ[m=0〜(n-1)]m*((m+1)^r-m^r) + n

=Σ[m=0〜(n-1)]((m+1)^(r+1)-m^(r+1))-Σ[m=0〜(n-1)](m+1)^r + n =n^(r+1)-(1^r+2^r+ … +n^r)+n.

よって，

a(n,2)=n^3-(1^2+2^2+ … +n^2)+n = n*(4*n^2-3*n+5)/6.

a(45,2)=59775.

a(n,3)=n^4-(1^3+2^3+ … +n^3)+n = n*(n+1)*(3*n^2-5*n+4)/4.

[設問3](与式) = 11*2^(48)+2 (答)

floor(k^(1/2))=m ⇔ m^2≦k<(m+1)^2 である．

nを正整数とするとき，

Σ[k=1〜n^2]2^floor(k^(1/2))

=(Σ[k=0〜n^2]2^floor(k^(1/2))) -1

=(Σ[m=0〜(n-1)]((m+1)^2-m^2)*2^m) + 2^n -1

=(Σ[m=0〜(n-1)](2*m+1)*2^m) + 2^n -1

=(Σ[m=0〜(n-1)]((2*m-1)*2^(m+1)-(2*m-3)*2^m)) + 2^n -1 =(2*n-3)*2^n + 3 + 2^n -1 =(n-1)*2^(n+1)+2.

n=45のときには，

Σ[k=1〜2025]2^floor(k^(1/2))

=(45-1)*2^(45+1)+2

=11*2^(48)+2.

[設問4](与式) = 5/6 (答)

(n/2-1)<floor(n/2)≦(n/2), (n/3-1)<floor(n/3)≦(n/3)

であるから，

((5/6)*n-2)<floor(n/2)+floor(n/3)≦(5/6)*n.

よって，

((5/6)-2/n)<(1/n)*(floor(n/2)+floor(n/3))≦(5/6).

lim[n→∞]((5/6)-2/n)=(5/6) であるから，はさみうちの原理より，

lim[n→∞](1/n)*(floor(n/2)+floor(n/3))=(5/6).

[追加問題1]

(乙の一辺の長さ)=(1/2)*(-1+5^(1/2))*c，

(短軸の長さ)=2*c*((3/10)*(5-5^(1/2)))^(1/2)　(答)．

xy直交座標を設定して考える．

楕円の中心を原点とし，問題図において甲の一辺が接している直線を

x軸とする．

楕円の方程式を，

(x/a)^2+(y/b)^2=1 (a>c, b>0) とする．この楕円は，2点 (c/2,(c/2)*3^(1/2)),

((1/2)*(a+c),(1/2)*(a-c)*3^(1/2)) を通過するから，

((c/2)/a)^2+((c/2)*3^(1/2)/b)^2=1 ---(1)

および

((1/2)*(a+c)/a)^2+((1/2)*(a-c)*3^(1/2)/b)^2=1 ---(2)

が成り立つ．

ここで，a=t*c (t>1), b=s*c とおいて(1)に代入して，

1/(4*t^2)+3/(4*s^2)=1 ---(3)

また，a=t*c (t>1), b=s*c を(2)に代入して，

(1/4)*(1+1/t)^2+(3/(4*s^2))*(t-1)^2=1 ---(4)

(3),(4)より，

t=(1/2)*(1+5^(1/2)),

s=((3/10)*(5-5^(1/2)))^(1/2) (=0.9105…).

(乙の一辺の長さ)=(a-c)=(t-1)*c=(1/2)*(-1+5^(1/2))*c.

s<1であるから，b<a.

(短軸の長さ)=2*b=2*s*c=2*c*((3/10)*(5-5^(1/2)))^(1/2).

[追加問題2]

(円C_1の半径)=(1/2)*(1+5^(1/2))+(5+2*5^(1/2))^(1/2),

(円C_2の半径)=(1/2)*(1+5^(1/2))*((1/2)*(5+5^(1/2))+(5+2*5^(1/2))^(1/2) )^(1/2),

(円C_3の半径)=(3+5^(1/2)+((1/2)*(25+11*5^(1/2)))^(1/2))^(1/2) (答)

1辺の長さがaであるような正n角形の外接円の半径をRとするとき，

R=(a/2)*csc((180/n)°).

円 C_1 は，1辺の長さが，図の線分BCの長さに等しいような

正10角形の外接円である．(図→ https://fpseries.exblog.jp/33512806/ )

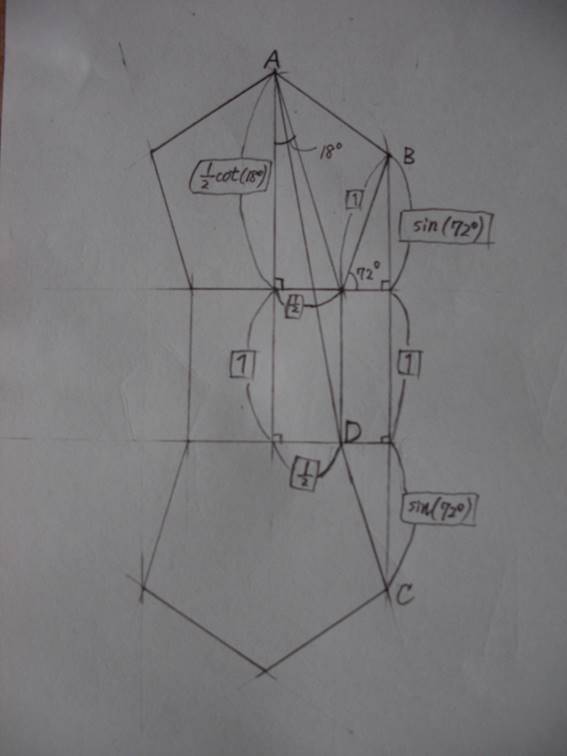
BC=2*sin(72°)+1.

(円C_1の半径)

=(1/2)*(BC)*csc(18°)

=(1/2)*(1+5^(1/2))+(5+2*5^(1/2))^(1/2).

(=4.69571…)

円 C_2 は，1辺の長さが，図の線分ADの長さに等しいような

正10角形の外接円である．

AD=(((1/2)*cot(18°)+1)^2+(1/2)^2)^(1/2).

(円C_2の半径)

=(1/2)*(AD)*csc(18°)

=(1/2)*(1+5^(1/2))*((1/2)*(5+5^(1/2))+(5+2*5^(1/2))^(1/2) )^(1/2).

(=4.186838…)

円 C_3 は，1辺の長さが1である正20角形の外接円である．

(円C_3の半径)

=(1/2)*(1)*csc(9°)

=(3+5^(1/2)+((1/2)*(25+11*5^(1/2)))^(1/2))^(1/2).

(=3.19622…)

---------------------------------

美しい数学の話の第59話に掲載されている

「大相撲の巴戦」

を一般化して考えてみました．

AがBに勝つ確率を p,

BがCに勝つ確率を q,

CがAに勝つ確率を r

とします．

A,B,Cが優勝する確率をそれぞれ，

A(p,q,r), B(p,q,r), C(p,q,r)

とします．

状態遷移図は図のようになります．

(図→ https://fpseries.exblog.jp/33520807/ )

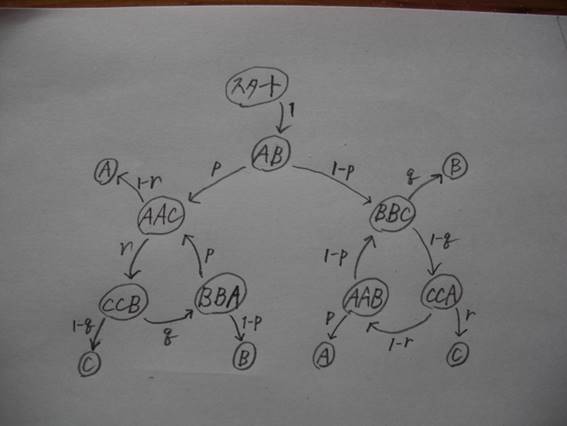
例えば，AAC はAとCの対戦であって，Aがこの対戦に勝てば

Aの優勝が決まるという状態を表しています．

以下，(AAC)というのは，AACという状態が生じる確率を表すものとします．

次のような連立方程式が成り立ちます．

(AB)=1,

(AAC)=p*(AB)+p*(BBA),

(CCB)=r*(AAC),

(BBA)=q*(CCB),

(BBC)=(1-p)*(AB)+(1-p)*(AAB),

(CCA)=(1-q)*(BBC),

(AAB)=(1-r)*(CCA).

これを解くと次のようになります．

(AAC)=p/(1-p*q*r),

(CCB)=r*p/(1-p*q*r),

(BBA)=q*r*p/(1-p*q*r),

(BBC)=(1-p)/(1-(1-p)*(1-r)*(1-q)),

(CCA)=(1-q)*(1-p)/(1-(1-p)*(1-r)*(1-q)),

(AAB)=(1-r)*(1-q)*(1-p)/(1-(1-p)*(1-r)*(1-q)).

よって，

A(p,q,r)

=(1-r)*(AAC)+p*(AAB)

=(1-r)*p/(1-p*q*r)+p*(1-r)*(1-q)*(1-p)/(1-(1-p)*(1-r)*(1-q)),

B(p,q,r)

=(1-p)*(BBA)+q*(BBC)

=(1-p)*q*r*p/(1-p*q*r)+q*(1-p)/(1-(1-p)*(1-r)*(1-q)),

C(p,q,r)

=(1-q)*(CCB)+r*(CCA)

=(1-q)*r*p/(1-p*q*r)+r*(1-q)*(1-p)/(1-(1-p)*(1-r)*(1-q))

となります．

また，優勝が決まるまでの総対戦数の期待値を E(p,q,r) とすると，

E(p,q,r)

=Σ[k=0〜∞](1+p+p*r)*(p*r*q)^k

+Σ[k=0〜∞](1+(1-p)+(1-p)*(1-q))*((1-p)*(1-q)*(1-r))^k

+(-1)

=(1+p+p*r)/(1-p*r*q)+(1+(1-p)+(1-p)*(1-q))/(1-(1-p)*(1-q)*(1-r))+(-1).

大相撲の巴戦については，様々な記事がありますね．

数研通信にも大相撲の巴戦について考察している記事がありました．

＜水の流れ：他のサイトの情報に感謝します。＞

＜水の流れ：さて、追加問題２のＣ２半径ですが

(円C_2の半径)=(1/2)*(1+5^(1/2))*((1/2)*(5+5^(1/2))+(5+2*5^(1/2))^(1/2) )^(1/2),に

この値が正しいか判断に迷っています。

「よふかしのつらいおじさん」の答えは

√(20+8√5+(4+2√5)√(10+2√5) ) /2 (=4.186838⋯)

です。表現が違いますが、近似値が合っていれば正解です。

「二度漬け白菜」 02/17 18時49分　 受信 更新 3/2

私の算出した(円C_2の半径)に対して，

「この値が正しいか判断に迷っています。」

とのことでした．

「よふかしのつらいおじさん」の答えであるところの、

√(20+8√5+(4+2√5)√(10+2√5) ) /2

という値が正しい答えであるとするならば，

私の算出した(円C_2の半径)も「正しい」ということになります．

なぜなら，この両者は完全に一致するからです．

このことは次のようにして示すことができます．

私の算出した(円C_2の半径)を A,

「よふかしのつらいおじさん」の答えを B

とします．すなわち，

A=(1/2)*(1+5^(1/2))*((1/2)*(5+5^(1/2))+(5+2*5^(1/2))^(1/2) )^(1/2),

B=(20+8*5^(1/2)+(4+2*5^(1/2))*(10+2*5^(1/2))^(1/2))^(1/2)/2

とします．

いまから，

(2*A)^2=(2*B)^2=(20+8*5^(1/2))+(520+232*5^(1/2))^(1/2)

であることを示します．

(2*A)^2

=((1+5^(1/2))^2)*((1/2)*(5+5^(1/2))+(5+2*5^(1/2))^(1/2))

=(1/2)*((1+5^(1/2))^2)*(5+5^(1/2))+(((1+5^(1/2))^4)*(5+2*5^(1/2)))^(1/2)

=(20+8*5^(1/2))+(520+232*5^(1/2))^(1/2).

(2*B)^2

=(20+8*5^(1/2))+(4+2*5^(1/2))*(10+2*5^(1/2))^(1/2)

=(20+8*5^(1/2))+((4+2*5^(1/2))^2*(10+2*5^(1/2)))^(1/2)

=(20+8*5^(1/2))+(520+232*5^(1/2))^(1/2).

よって，(2*A)^2=(2*B)^2 が示せました．

これで，A=B であることがわかります．

＜水に流れからお詫び：円C_2の半径ですが、二人の答えが同じであることが鮮明になりました。お騒がせしてしました。＞
NO5「kasama」 02/23 14時52分　　 受信 更新 3/2

「kasama」 02/25 09時26分　　 受信 更新 3/2

前回から一部修正された解答です

NO6「三角定規」 02/24 18時45分　 受信 更新 3/2

「三角定規」 02/25 18時28分　 受信 更新 3/2

前回から一部修正された解答です

《追加2》については,「多重根号はいろいろな簡約の仕方があるものだ！」と実感です。同値性をすべて確認しました。

「水の流れ」 更新 3/2

　

皆さん、問題や質問に答えてください。一部でも構いませんから, 解答とペンネームを添えて, メールで送ってください。待っています。