令和３年５月２日

[流れ星]

　　第399回数学的な連続応募解答

　　　　＜解答募集期間：４月４日〜５月2日＞

　　　　　　　　［明星輪寺の算額(２)］

第359回の応募問題は元治２年（1865）に大垣市の明星輪寺に奉納された算額で、初ノ段、四ノ段、八ノ段の問題を出題しました。

今回は、その続きで、二ノ段、五ノ段の問題です。

　問題１　ひし形の中に交わる赤円が２個、白円が２個、青円が５個接している。白円の直径が与えられたとき、青円の直径を求めよ。

　　　　　　　　　　　　　　　　　　　　　　　　　　

出題者　山崎継次郎

 

術文（答）青円の直径は白円の直径÷２

 

 

 

問題２　台形内に半青円を作る。ただし青円の半径は台形の底辺の半分である。その中へ赤、白、黄、浅青、緑円の合計７個の円を入れる。赤の直径が与えられたときに緑の円の直径を求めよ。　　　　　　　　　　　　

出題者　細川荘六幸次　

 

 

 

 

 

 

 

 

 

 

 

 

術文（答）

緑円の直径は赤円の直径÷５

 

＜水の流れ：この問題を解くには、台形と白円、浅青円は不要です＞

 

 

 

追加問題１（提供者「三角定規」さん）

過日マーケットで雛あられを買ったところ，添付図のような不思議な形の箱に入っていました。

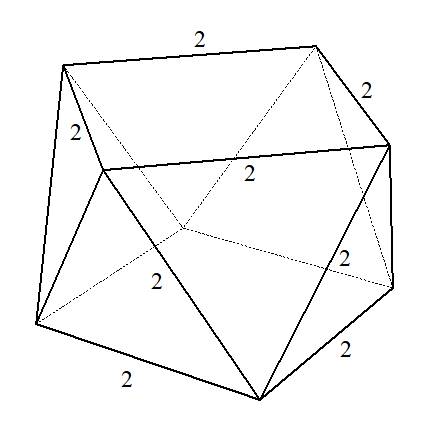
上下の底面は正方形，側面は８つの正三角形が上下交互に並んでいて，また２つの正方形は上から見て一方が45°回転しています。私は初めて見る形で「こんな立体があるんだ」と驚き，感心しました。そこで，

 

［問題］１辺を 2 とし，この立体の体積を求めよ。

菓子箱

追加問題（提供者　ジョーカーさん）　

　b_20

 

NO1「スモークマン」     4/05     19時55分　     受信  更新 5/2

追加問題1

 

上と下の面が8角形になるようにして出っ張った３角錐8個を引く…

上の面の面積=2^2+(√2-1)*4=4√2

高さを求める…

(√3)^2-(√2-1)^2=2√2=√8=(8^(1/4))^2

so…高さ=8^(1/4)

出っ張った３角錐の体積=(√2-1)*8^(1/4)/3

so…

4√2*8^(1/4)-8*(√2-1)*8^(1/4)/3

=(1/3)(4√2+8)*8^(1/4)  =7.655999854693733 < 2^3 だからいいような？

 

追加問題2

 

x%遅刻したとすると…

x=x*0.1+(100-x)*0.3

1.2*x=30

so…x=30/1.2=100/4=25%

 

NO2「ジョーカー」    　 4/05     22時43分       受信  更新 5/2

　ジョーカーさんのすべての解答です。

 

NO3「三角定規」　　　　 4/06     19時23分　　　 受信  更新 5/2

　　三角定規さんの追加問題１の解答です

 

「三角定規」　　　　 4/07     10時33分　　　 受信  更新 5/2

　　三角定規さんの解答です

　　三角定規さんの追加問題２の解答です

NO4「よふかしのつらいおじさん」 4/11 21時21分　   受信  更新 5/2

 

問題１

●2個の赤円の中心をE、Fとします。

 

直線ACに赤円と青円2個が接しています。

どの青円も大きさが等しいので、接点間の距離が等しくAB＝BCです。

また、AD、BE、CFが平行なので、DE＝EFです。

 

各円の半径を、青：b、赤：r、白：wとします。

外接した青円と白円が、赤円に内接しているので、2r＝2b＋2wより、r＝b＋wです。

 

DEは、青円と赤円の半径の和なので、DE＝b＋r＝b＋(b＋w)＝2b＋w

EFは、GH(白円、青円、白円の直径の和)からGEとFH(赤円の半径)を引いたものなので、

EF＝GH−GE−FH＝2w＋2b＋2w−r−r＝4w＋2b−2r＝4w＋2b−2(b＋w)＝2w

 

よって、b＝w／2となり、青円の直径は白円の直径の半分です。

 

 

問題2

●Rを赤円の中心、Sを赤円と青円の接点とします。

半径を青円：ｂ、赤円：ｒ、とします。

△OHRは直角二等辺三角形なので、 です。

 

 

●Yを黄円の中心とします。

半径を黄円：ｙとします。

△YHRは直角三角形です。

 

●青円と黄円の接点Tを中心として赤円を反転してみます。

このとき、 とします。(2bは青円の直径です)

青円の直径は2ｂなので、青円は、Tからの距離が2ｂの青直線に反転されます。

黄円の直径は2ｙなので、Ｔからの距離が の黄直線に反転されます。

赤円は、青円と黄円に接していたので、青直線と黄直線に接する円に反転されます。

反転された赤円の半径は、 です。

△THR∽△TH’R’なので、

 

(3)を(2)に代入すると、

 

●緑円の半径をmとします。

デカルトの円定理を用いると、黄円(ｙ)、緑円(ｍ)、赤円(ｒ)、青円(ｂ)の半径には次の関係があります。

 

この式に(1)、(4)を代入します。

m≠rなので

つまり、緑円の半径は、赤円の5分の1です。

 

 

 

追加問題1

●左の立体を真上からみて、上の正方形と下の正方形を重ねた図が右です。

正方形の頂点をつないだ赤の図形は正8角形です。

 

●底面に垂直な赤の正８角形の辺を含む８個の平面でこの図形を覆ってみます。

すると正８角柱ができます。(左の図)

 

次にピンクの三角形を底面とする三角錐ABCD、空色を底面とする三角錐EFDB注目します。

この２個の立体は合同です。

これに合同な立体は、全部で８個あります。

 

●問題の体積を求めます。

 

正8角形の辺ABの長さを求めます。

、 なので、

正8角柱の体積Vは、底面積S、高さADとして、

 

8個の三角錐の体積V‘を求めます。

底面積をS‘、高さADとして、

 

ゆえに、求める体積は、

 

 

追加問題2

●ある生徒がｎ日目にきちんと登校した確率をｐn、遅刻した確率をｑnとします。

ｐn＋ｑn＝1です。

連続した2日の関係を式で表してみます。

 

●行列の計算をします。

とおき、対角化します。

より、

固有値は、 

固有ベクトルは、 のとき、 より、

固有ベクトルは、 のとき、 より、

よって、、、

 

 

 

 

１／４なので、25％遅刻する。

 

皆さん、問題や質問に答えてください。一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。