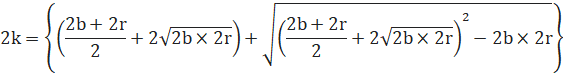令和4年8月21日
 [流れ星]
[流れ星]
第416回数学的な連続応募解答
<解答募集期間:7月24日〜8月21日>
[大垣八幡宮奉納算額9]

岐阜県大垣市にある八幡神社
江戸時代末期、谷松茂(幽斎)は大垣藩士で致道館講官であった水野民興に学び、自ら塾を開いて和算を教えていました。彼の門人達が大垣市の八幡神社に天保年間に算額(絵馬)を奉納しています。この算額は残念ながら先の戦争で神社ごと焼失したことを知り、幽斎算約四編である奉納された算額の解法を後世に残すために、これから32問順に出題していきます。
今回は第19問題から第21問題です。
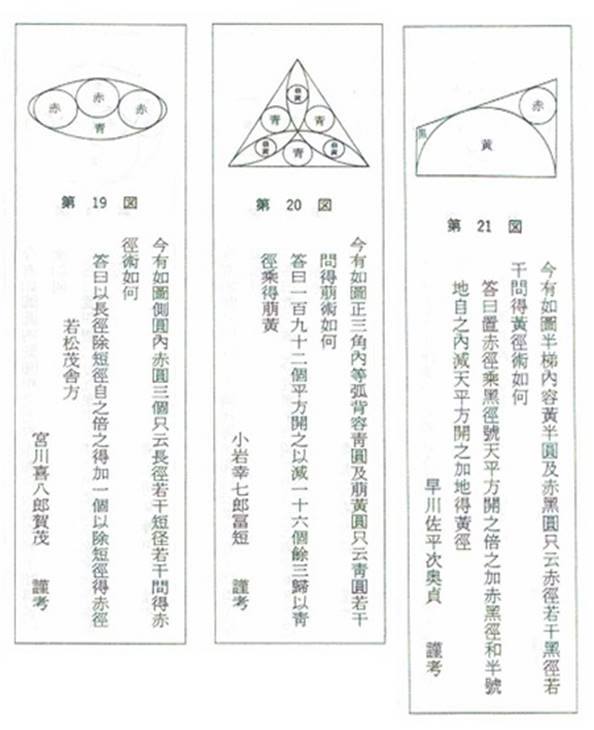
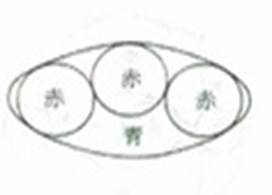
第19問題
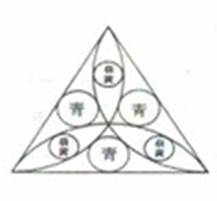
与えられた楕円(青)に3個の等円(赤)を容れるとき赤円の直径を求めよ 。出題者 宮川喜八郎賀茂 謹考
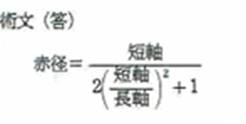
第20問題
正三角形内に等しい3孤を描いてその内に3個ずつ青円、萌黄円を容れる。青円の直径を知って、萌黄円の直径を求めよ。
出題者 小岩幸七郎冨短 謹考
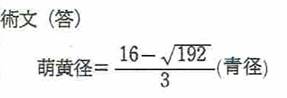
第21問題
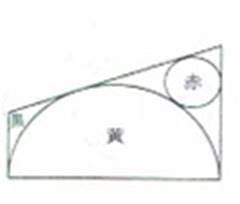
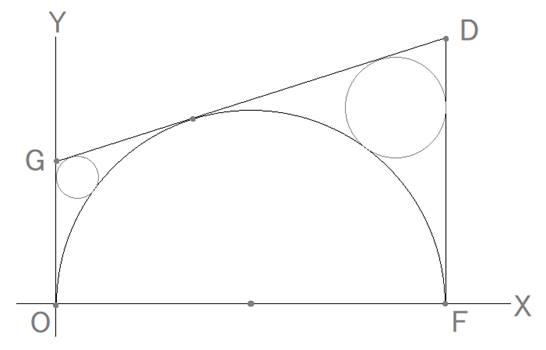
梯形内に半円(黄)を作りその内に赤円、黒円を内接させる。
赤円と黒円の直径を知って黄円の直径を求めよ。
出題者 早川佐平次奥貞 謹考

追加問題(ジョーカーさん提供)
4次方程式x4+68x3+kx2―4930x+2023=0 について、
4つの解のうち2つの解の積が―17であるとき、次の問に答えよ。
(1)実定数kの値を求めよ。
(2)方程式の解を求めよ。
NO1「ジョーカー」 07/24
09時31分 受信 更新 8/21
寄せられた大垣八幡宮奉納算額の第19問から第21問の解答です
また、追加問題の解答です.
NO2「よふかしのつらいおじさん」07/27 22時11分 受信 更新 8/21
第19問題
●楕円の方程式を、![]()
中央の円の方程式を、![]()
右の円の方程式を、![]()
とします。
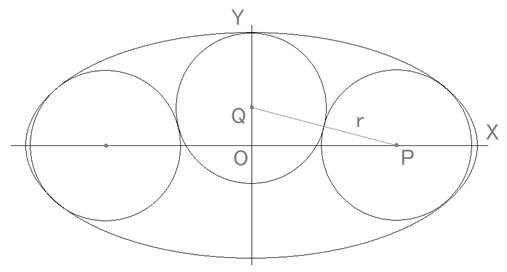
△OPQに三平方の定理を用いると、
![]()
ここで、![]() を消去すると、
を消去すると、
![]()
●右の円と楕円が接するので(D=0)、
![]()
![]()
判別式Dをとって、
![]()
![]()
![]()
Pを代入して、
![]()
![]()
![]()
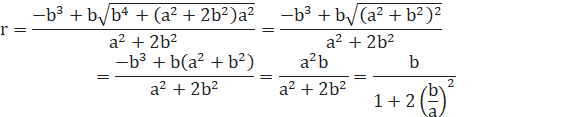
ゆえに、
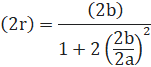
第20問題
●円弧の半径をR、青円の半径をb、萌黄円の半径をmとします。
三角形ABCは、内角が30°、60°、90°なので、![]() です。
です。
また、![]() なので、
なので、![]() です。
です。
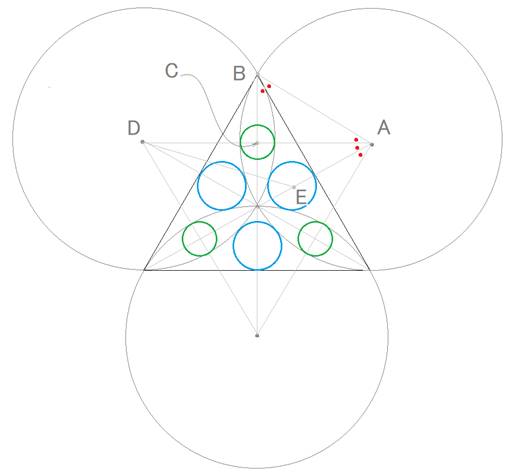
●△ADEに余弦定理を用いると、∠DAE=30°なので、
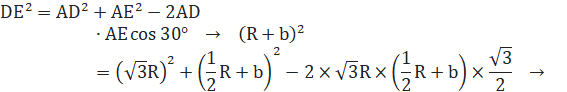

ここで、Rをmで表します。
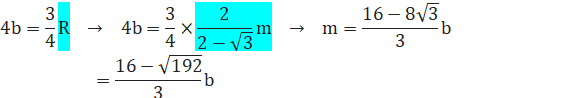
ゆえに、
![]()
第21問題
●黄半円の半径をk、赤円、黒円の半径をそれぞれr、bとします。
図の△ABCと△BDEは相似です。
![]() なので、
なので、![]()
よって、![]() です。
です。
GJの長さは、上の結果のrをbに変えて、![]() です。
です。
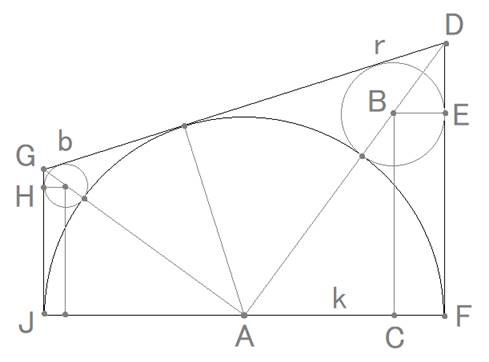
●上の図形を下のように置きます。
必要な点の座標は、
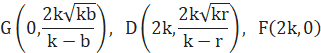
よって、直線GDの方程式は、
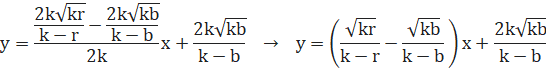
黄色円Kの方程式は、![]()
●黄色円Kと直線GDを連立させます。
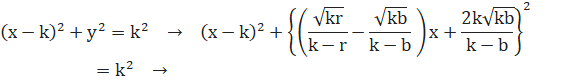
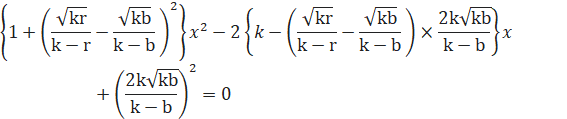
直線と円とは接するので、判別式D=0 とします。
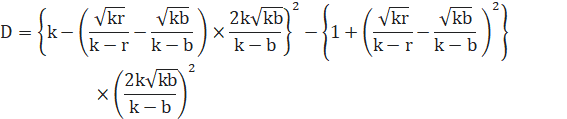
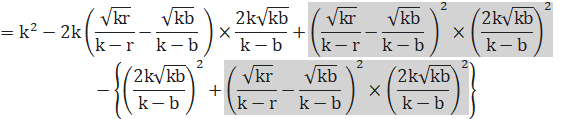
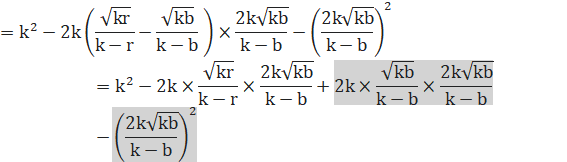
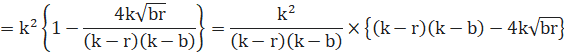
![]()
kは、0、r、bではないので、黄色の部分の2次方程式として、
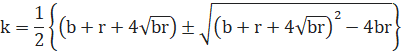
kは、bやrに比べてだいぶ大きいので、複合は「+」を選んで、
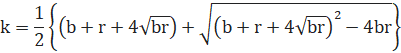
よって、
![]() を水色、
を水色、
![]() を緑色とすれば、
を緑色とすれば、
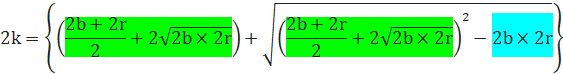
追加問題
●
![]()
4個の解を、![]() とします。
とします。
するとこの4次方程式は、
![]()
![]()
ここで、![]() とします。
とします。
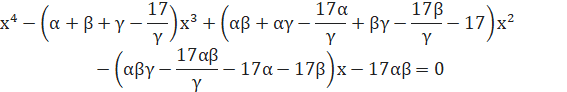
![]()
![]()
![]()
![]()
(4)より、![]()
![]()
(3)にいれて、
![]()
![]()
(1)’+(3)’よりαを消去して、
![]()
![]()
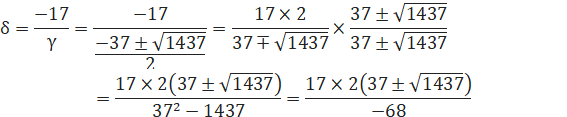
![]()
●ここで、
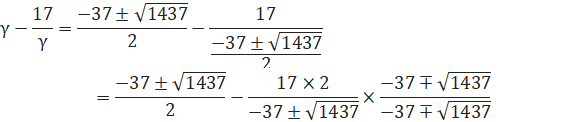
![]()
![]()
より(1)’は、
![]()
![]()
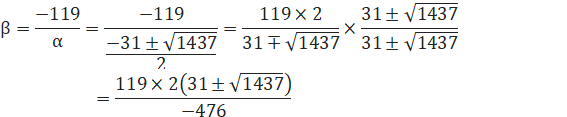
![]()
●
![]()
![]()
なので(2)は、
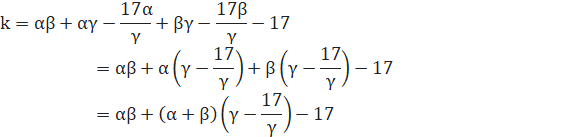
![]()
以上から、
(1)![]()
(2)方程式の解は、
![]()
「よふかしのつらいおじさん」07/31 14時12分 受信 更新 8/21
追加問題の別解
●
![]()
4個の解を、![]() とします。
とします。
するとこの4次方程式は、
![]()
![]()
![]() とすると、
とすると、![]() なので、(2)を、
なので、(2)を、
![]()
とします。
展開すると、
![]()
ゆえに、
![]()
![]()
(3)と(5)を連立させると、![]() 。
。
(1)よって(4)に代入して、![]()
(2)![]() に代入して、
に代入して、
![]() より、
より、
![]()
NO3「三角定規」 08/16
15時34分 受信 更新 8/21
寄せられた第19問から第21問の解答です
「三角定規」 08/16
22時46分 受信 更新 8/21
また、追加問題の解答です.
皆さん、問題や質問に答えてください。一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。