�ߘa�T�N�S��28��
 [���ꐯ]
[���ꐯ]
�@�@��424�����w�I�ȘA�������
�@�@�@�@����W���ԁF�R���T���`�S���Q����
�m�ŏ��l�E�ő�l�n

�lj����u�W���[�J�[�v�����
��417��́u���O�p�`�̕ӂ�~�ʂɂ���Ĉ͂܂ꂽ�}�`���̂S�~�v
�V���[�Y�͋x�܂��Ă��������܂��B
NO1�u�W���[�J�[�v �@03/05 �@�@
11��54�� ��M �X�V 4/2
��ꂽ����������
�u�W���[�J�[�v �@03/05 �@�@
20��46�� ��M �X�V 4/2
��ꂽ���Q���ʉ��ł��B
NO2�ukasama�v
03/12
23��46���@ ��M �X�V 4/2
��ꂽ����������
�ukasama�v
03/17
18��13���@ ��M �X�V 4/2
�@
���P�́i�R�j�@�y�⑫�z2023/03/17�NjL
�X��m�̎Z�o�́A�����i�~�̐ڐ��̕������j���g���A�����ƊȒP�ɋ��߂��܂��B
�~�@��̓_![]() �̐ڐ��͎����ŕ\����܂��B
�̐ڐ��͎����ŕ\����܂��B
![]()
����ƁA![]() ���~�@��̓_�ł��邱�ƂƁA�ڐ�����_
���~�@��̓_�ł��邱�ƂƁA�ڐ�����_![]() ��ʂ邱�Ƃ��A
��ʂ邱�Ƃ��A
![]()
![]()
�����������ƁA
![]()
�Ȃ̂ŁA�X��m��

�ł��B
(3)�_![]() �A�_
�A�_![]() ���x�N�g��
���x�N�g��![]() �A
�A![]() �Ƃ����Ƃ��A����
�Ƃ����Ƃ��A����![]() ��
��![]() �ł��邱�ƂɋC�t���A����Ȃ������Ǝv���܂��B
�ł��邱�ƂɋC�t���A����Ȃ������Ǝv���܂��B
|
|
�}�̂悤�ɁA
�ł��B����ƁA |
|
|
|
|
�~�A�̔��a��3�Ȃ̂ŁA
�~�@�̔��a��10�Ȃ̂ŁA
|
�~�A�̔��a��3�Ȃ̂ŁA
�~�@�̔��a��10�Ȃ̂ŁA
|
����āA���߂�ŏ��l�E�ő�l�͂��ꂼ��ȉ��̒ʂ�ł��B
![]() �̂Ƃ�-70
�̂Ƃ�-70
![]() �̂Ƃ�70
�̂Ƃ�70
���Q�@�y�ʉ��z2023/03/17�NjL
![]() �A
�A![]() �����a1�̉~����̓_�ł��邱�ƂɋC�t���A�~�Ɛڐ��̖��ɋA���ł��܂��B
�����a1�̉~����̓_�ł��邱�ƂɋC�t���A�~�Ɛڐ��̖��ɋA���ł��܂��B![]() �A
�A![]() �Ƃ����A���P��(2)�Ƃقړ����ł��B
�Ƃ����A���P��(2)�Ƃقړ����ł��B
|
|
�Ƒ����āA��_ |
�~����̓_![]() �̐ڐ��͎����ŕ\����܂��B
�̐ڐ��͎����ŕ\����܂��B
![]()
����ƁA![]() ���~��̓_�ł��邱�ƂƁA�ڐ�����_
���~��̓_�ł��邱�ƂƁA�ڐ�����_![]() ��ʂ邱�Ƃ��A
��ʂ邱�Ƃ��A
![]() ����@
����@
![]() ����A
����A
������![]() �͈͓̔��ʼn����ƁA
�͈͓̔��ʼn����ƁA
![]()
�ł��B����ƁA�X��m��

�ł��B�ȏ���A���߂�ŏ��l�E�ő�l�͂��ꂼ��1�A![]() �ł��B
�ł��B
���R�i�P�j�y�ʉ��z2023/03/17�NjL
![]() ��
��![]() ���Ȑ��ƌ���Δ����ł����@�ȊO�͕����Ȃ��̂ł����A2�_�Ԃ̒�����\�����Ă��邱�ƂɋC�t���ΈĊO�ȒP�ł����B�^����
���Ȑ��ƌ���Δ����ł����@�ȊO�͕����Ȃ��̂ł����A2�_�Ԃ̒�����\�����Ă��邱�ƂɋC�t���ΈĊO�ȒP�ł����B�^����
![]()
![]()
�ƕό`����A���ꂼ��_![]() �Ɠ_
�Ɠ_![]() �̒����A�_
�̒����A�_![]() �Ɠ_
�Ɠ_![]() �̒����ƌ����Ă邱�Ƃ��ł��܂��B
�̒����ƌ����Ă邱�Ƃ��ł��܂��B
|
|
���}�̒ʂ�A�^���͐Ԑ��ƃI�����W���𑫂����킹������ABC�̒����ƍl���邱�Ƃ��ł��܂��B |
����ABC���ł��Z���Ȃ�̂́A�_A�AB�AC���꒼����ɂ���Ƃ��ł��B
|
|
�}�œ_C�����߂�̂��ȒP���Ǝv���܂��B ����AB�́A
�Ȃ̂ŁAx���Ƃ̌�_��
�ł��B |
�ȏ���A![]() �ōŏ��l
�ōŏ��l![]() ���Ƃ�܂��B
���Ƃ�܂��B
���R�i�Q�j�y�ʉ��z2023/03/17�NjL
(1)�Ɠ����悤�ɂ��A�Δ����݂����ȑ����U���Ȃ��Ƃ����w�̐��w�ʼn����܂��ˁB�^�����_����̒����ƌ����ĂāA

�ƕό`���܂��B�܂�A��蕶��![]() ��
��![]() ��
��![]() ��
��![]() �ƒH�����Ƃ��̌o�H�̍ŏ��l�Ɠǂݑւ��邱�Ƃ��ł��܂��B
�ƒH�����Ƃ��̌o�H�̍ŏ��l�Ɠǂݑւ��邱�Ƃ��ł��܂��B
|
|
�}������ƁA���}�̂悤�ɂȂ�܂��B �X��A�_A�AB�AC�AD�Ƃ��܂��B |
����ABCD���ł��Z���Ȃ�̂́A�_A�AB�AC�AD���꒼����ɂ���Ƃ��ł��B
|
|
�}�ł��̂��ȒP���Ǝv���܂��B ����AD�́A
�Ȃ̂ŁAx���Ƃ̌�_��
�ł��B |
�ȏ���A![]() �̂Ƃ��A�ŏ��l��
�̂Ƃ��A�ŏ��l��![]() �ł��B
�ł��B
���R�i�R�j�y�ʉ��z2023/03/17�NjL
�W���[�J�[����̃I���W�i�����Ŏ��g�݂܂����B
��{�I�ɂ�(1)�Ɠ����悤�ɂ��Ηǂ��̂ł����A�����H�v����Όv�Z���y�ɂȂ�܂��B![]() ��y���Ɋւ��đΏۂȂ̂ŗ̈�
��y���Ɋւ��đΏۂȂ̂ŗ̈�![]() �ł��Ηǂ��ł��i�K�v�Ȃ�A�̈�
�ł��Ηǂ��ł��i�K�v�Ȃ�A�̈�![]() �̌��ʂ��~���[����Ηǂ��j�B�܂��A������ς��Ȃ���A�K���ȕϊ�(���^�ʑ�)���{���Ă��\���܂���A
�̌��ʂ��~���[����Ηǂ��j�B�܂��A������ς��Ȃ���A�K���ȕϊ�(���^�ʑ�)���{���Ă��\���܂���A![]() �Ő܂�Ԃ��܂��B
�Ő܂�Ԃ��܂��B

���̉��߂ł����ƁA��蕶�́w2��_![]() �A
�A![]() �ɑ��āA
�ɑ��āA![]() ��ɓ_P���Ƃ�B
��ɓ_P���Ƃ�B![]() �̍ŏ��l�Ƃ��̂Ƃ��̓_P��x���W�����߂�x�Ɠǂݑւ��邱�Ƃ��ł��܂��B
�̍ŏ��l�Ƃ��̂Ƃ��̓_P��x���W�����߂�x�Ɠǂݑւ��邱�Ƃ��ł��܂��B
�_![]() �Ƃ���ƁA
�Ƃ���ƁA
![]()

�Ȃ̂ŁA![]() �̍ŏ��l�͓_
�̍ŏ��l�͓_![]() ��
��![]() ��
��![]() ��H�����Ƃ��A���̌o�H�̍ŏ��l�����߂�̂Ɠ����ł��B
��H�����Ƃ��A���̌o�H�̍ŏ��l�����߂�̂Ɠ����ł��B
|
|
���� |
����S�fXE���ł��Z���Ȃ�̂́A�_S�f�AX�AE���꒼����ɂ���Ƃ��ł��B
|
|
����S�fE�́A
�� �Ȃ̂ŁAx���Ƃ̌�_��
�ł��B |
�ȏ���A���̖�蕶�ɖ߂��ĕ\������ƁA![]() �̍ŏ��l��
�̍ŏ��l��![]() �ŁA�_P��y���W��
�ŁA�_P��y���W��![]() �ł��B
�ł��B
�㎮��![]() �A
�A![]() �������ƁA�ȉ��̒ʂ�ł��B
�������ƁA�ȉ��̒ʂ�ł��B
![]() �̍ŏ��l=
�̍ŏ��l=
�_P��y���W=![]()
NO3�u�X���[�N�}���v 03/08
22��22���@ ��M �X�V 4/2
(1)
(11)
(x-3)^2+(y-4)^2=4
x^2+y^2+2x-2y
=(x-3)^2+(y-4)^2+6x+8y-9-16+2x-2y
=8x+6y-21=k
So�c�~�̒��S���炱�̒����܂ł̋���
|24+24-21-k|/��(8^2+6^2)=2
|27-k|=20
k=7 or 47
so�c
Max=47, Min=7
(12)
(y-1)/(x+1)
x-3=2cos��-4
y-4=2sin��
(y-1)/(x+1)=(2sin��+3)/(2cos��+4)
((2sin��+3)/(2cos��+4))�f
=(3sin��+4cos��+2)/(2(cos��+2)^2
=(5sin(��+��)+2) /(2(cos��+2)^2
3sin��+4cos��=-2
sin^2��+cos^2��=1
3y+4x=-2
x^2+y^2=1
x=cos��=(-1/25)(8�}3��21)
y=sin��=(1/25)(-6�}4��21)
so�c
(y-1)/(x+1)
=(2sin��+3)/(2cos��+4)
=(2*(1/25)(-6+4��21)+3)/(2*(-1/25)(8+3��21)+4)=(1/6)(6+��21)�E�E�EMax
=(2*(1/25)(-6-4��21)+3)/(2*(-1/25)(8-3��21)+4)=(1/6)(6-��21)�E�E�EMin
(13)�@
ac+bd
(a,b)=(2cos��+3,2sin��+4)
(c,d)=(cos��,sin��)
ac+bd
=(2cos��+3)*cos��+(2sin��+4)*sin��
=2(cos��*cos��+sin��*sin��)+3cos��+4sin��
=2cos(��+��)+5*sin(��+��)
=2cos(��+��)+5sin(��+��)
=��29*sin(��+��)
So�c
Max=��29
Min=-��29
�����̗���F(c,d)=(�P�Ocos��,�P�Osin��)�ł��B�������ł���́H�B��
(2)
((sin��+3)/(cos��+2))�f=(3sin��+2cos��+1)/(cos��+2)^2
So�c
3sin��+2cos��=-1
3y+2x=-1
x^2+y^2=1
x=(1/13)(-2�}6��3)
y=(-1/13)(3�}4��3)
so�c
(y+3)/(x+2)
=((-1/13)(3+4��3)+3)/( (1/13)(-2+6��3)+2)=(2/3)(3-��3)�E�E�EMin
=((-1/13)(3-4��3)+3)/( (1/13)(-2-6��3)+2)=(2/3)(3+��3)�E�E�EMax
�����̗���F�O�������Ɛ���������܂���
(3)
(31)
��(x^2+4x+8)+��(x^2-6x+10)
=��((x+2)^2+4)+��((x-3)^2+1)
(-2,2),(3,1)�̊Ԃ̋����Ȃ̂Łc
(3+2)^2+(1-2)^2=5^2+1=26
So�cMin=��26
�����̗���F�ɂ����@(-2,2),(3,�\1)�̊Ԃ̋����ł���
(32)
��(x^2-6x+13)+��(x^2+y^2)+��(y^2-8y+17)
=��((x-3)^2+4)+��(x^2+y^2)+��((y-4)^2+1)
(x-3)^2+4=x^2+y^2=(y-4)^2+1
(x-3)^2+4=(x-3)^2+(y-4)^2+6(x-3)+8(y-4)+25=(y-4)^2+1
X^2+4=X^2+Y^2+6X+8Y+25=Y^2-1=t
2t-5+6X+8Y+25=t
t=-6X-8Y-20
so�c
X^2+Y^2+5=-2(6X+8Y+20)
X^2+12X+Y^2+16Y=-45
(X+6)^2+(Y+8)^2=36+64-45=55
(-6.-8) ����A6X+8Y+20+t=0 �ւ̋�������55
|-36-64+20+t|/��(6^2+8^2)<=1
-10<=-80+t<=10
70<=t<=90
Min{t}=70
So�c
Min{�^��}=3��70
�����̗���F�l�������H��
(33)
(p,p^2), (0,17/4),(0,5/4)
��(p^2+(p^2-17/4)^2)+��(p^2+(p^2-5/4)^2)
So�c
(0,17/4)��(2p,5/4) ��ʂ钼��
y-17/4=(-3/(2p))*x
��(p,p^2)��ʂ�
p^2-17/4=-3/2
p^2=11/4
so�c
(0,17/4)��(��11,5/4)�Ƃ̋���
=��(11+3^2)
=2��5
�����̗���F�l�������H��
�u�X���[�N�}���v 03/13
14��32���@ ��M �X�V 4/2
�čl�������̂ł�...Orz
(13)
ac+bd
=(a,b)(c,d)cod��
=��(a^2+b^2)*��(c^2+d^2)*cos��
=2*10sin��
�}��`���Ă݂�Ɓc
2�̉~����̓_�܂ł̃x�N�g���̕��������ɂȂ邱�Ƃ͂Ȃ��A�������������܂�
So�c
Max=��20
Min=0
�����̗���F���a10�̉~�̏ꍇ�͑�3�ی��܂ōl���Ă��܂����甽������܂��BP�ia�Ab�j,�p�i���A���j�Ƃ��āA�x�N�g���n�o�̑傫���́@�x�N�g���n�p�̑傫�����l���ā�
��
(2)
(sin��+3)/(sin��+2)
(-2,-3)��x^2+y^2=1 ��̓_���������̌X�� :m
�����Ȃ�ƁA(-2,-3)���� �~�ւ̐ڐ��̌X�����̂���
�ڐ��Fy+3=m(x+2)
So�c
|3-2m|=��(m^2+1)
(3-2m)^2=m^2+1
3m^2-12m+8=0
3(m-2)^2=-8+12=4
So�c
m=2�}2/��3=2�}2��3/3
����
Max=2+2��33
Min=2-2��3/3
�����̗���F�����͈͂��㔼�~�ł�����A�ړ_����P�C�Q�ی��ł��B�ᖡ����
(3)
(31)
��(x^2+4x+8)+��(x^2-6x+10)
=��((x+2)^2+4)+��((x-3)^2+1)
(x,0) ��(-2,�}2), (3,�}1)�܂ł̋����̘a
�܂�A(-2,2)��(3,-1) or (-2,-2)��(3,1)�̌�_
5*(2/3)=10/3
��_(-2+10/3,0)=(4/3,0)�̂Ƃ������ɂȂ�̂�
�܂�Ax=4/3 �̂Ƃ�
Min=��{(3-(-2))^2+(-1-2)^2}=��34
(32)
under consideration...
(33)
�������ʂŔ��˂����Ƃ��̋������ŒZ�ɂȂ�͂��Ȃ̂Łc���̓_��P�Ƃ����
PA�̌X��+PB�̌X��=P�ł̖@���̌X���̂Q�{�Ȃ̂Łc
(p,p^2)
y=2p*x
y=(-1/(2p))*x
((p^2-17/4)/p+(p^2-5/4)/p)/(1-(p^2-17/4)(p^2-5/4)/p^2)
=(-1/p)/(1-1/(2p)^2)
(4p^2-7)/((2p-1)(16p^4-104p^2+85))=0
p��1/2, (1/2)��(13�}2��21) �̂Ƃ�
p=�}��7/2
��(7/4+(7/4-17/4)^2)+��(7/4+(7/4-5/4)^2)
=3��2=4.242�c�E�E�E���̂Ƃ����ŒZ�ŁAp^2=7/4
��((1/2)^2+(1/4-17/4)^2)+��((1/2)^2+(1/4-5/4)^2)
=(1/2)(��65+��5)=5.149�c
��(((1/2)��(13+2��21))^2+(((1/2)��(13+2��21))^2-(17/4))^2)
+��(((1/2)��(13+2��21))^2+(((1/2)��(13+2��21))^2-5/4)^2)
=7.579�c
��(((1/2)��(13-2��21))^2+(((1/2)��(13-2��21))^2-(17/4))^2)
+��(((1/2)��(13-2��21))^2+(((1/2)��(13-2��21))^2-5/4)^2)
=4.455�c
�u�X���[�N�}���v 03/31 22��35���@ ��M �X�V 4/2
�x���Ȃ�܂���(���荞��...) Orz
����ƍl���鎞�Ԃ����܂����̂ōčl���Ă݂܂��� ^^;
(13)
�}�ōl�����...
ac+bd
=(a,b)(c,d)cod��
So�c
Max=(5+2)*10=70
Min=-(5+2)*10=-70
�ł������c^^;
(2)
(sin��+3)/(sin��+2)
(-2,-3)��x^2+y^2=1 ��̓_���������̌X�� :m
�����Ȃ�ƁA(-2,-3)���� �~�ւ̐ڐ��̌X�����̂���
�ڐ��Fy+3=m(x+2)
So�c
|3-2m|=��(m^2+1)
(3-2m)^2=m^2+1
3m^2-12m+8=0
3(m-2)^2=-8+12=4
So�c
m=2�}2/��3
Min�͐}����A(-2,-3)��(1,0)�Ƃ����Ԓ����̌X��
Max��(-2,-3)����~ x^2+y^2=1 �ւ̐ڐ��̌X��
So�c
Min=(0-(-3)/(1-(-2)=3/3=1
Max�͏�ŋ��߂����̕��Ȃ̂�
Max=2+2��33
(32)
��������
�q���g�`�i�R�C�|�Q�j�@�a�i�|�P�C�S�j�C�@�@�o�i���C�O�j�@�C�@�p�i�O�C���j
�Ƃ����āA�l���Ă��������B
�E�E�E�ʔ������z�ł��ˁ�
A(3,-2)
B(-1,4)
����AB��x,y���̌�_���l����A�����̂̋����̘a=����AB�̒���
�ɂȂ�킯�ł����� ^^;
So�c(3+1)^2+(-2-4)^2=4^2+6^2=52
So�c2��13
(33)
�搶�̃q���g���悭�킩��Ȃ��������̂� ^^;
�����I��...
�������ʂŔ��˂����Ƃ��̋������ŒZ�ɂȂ�͂��Ȃ̂Łc���̓_��P�Ƃ����
PA�̌X��-�@���̌X��=�@���̌X��+PB�̌X���Ȃ̂Łc
PA�̌X��-PB�̌X��=2*�����̌X��
(p,p^2)
y=2p*x
y=(-1/(2p))*x
so�c�@���̌X��=-1/(2p)
AP�̌X��=(p^2-17/4)/p
BP�̌X��=(5/4-p^2)/p
So�c
{(17/4-p^2)/p-(p^2-5/4)/p}/(1+(17/4-p^2)(p^2-5/4)/p^2)
=2*(1/(2p))/(1-1/(4p^2))
(4p^2-7)/{(2p-1)(16p^4-104p^2+85)}=0
So�cp=�}��7/2
P=(�}��7/2,0)
AP+BP=��{(��7/2)^2+(17/4-7/4)^2}+��{(��7/2)^2+(5/4-7/4)^2}=3��2
�����̗���F�d�Ȃ鉞��ɔ�₵������J�Ǝ��Ԃɐ[�����ӂ��܂��B��
NO4�u��ӂ����̂炢��������v3/22 20��42�� ��M �X�V 4/2
�ꕔ���̓~�X�����܂����̂ŁA�����B
�u��ӂ����̂炢��������v3/26 21��58��
��M �X�V 4/2
�O��ꕔ�lj���[������A�����ɐV�����f�ڂ��܂��B
���1
(1)
��
![]() �Ƃ����܂��B
�Ƃ����܂��B
![]()
![]()
s���_ ![]() �Ɖ~�@�̎���̓_�Ƃ̋�����2������萔2���������l�ł��B
�Ɖ~�@�̎���̓_�Ƃ̋�����2������萔2���������l�ł��B
����āAs�̍ő�E�ŏ��͎���̓_���b�Ɖ~�@�̒��S ![]() ����������ɂ���Ƃ��ł��B
����������ɂ���Ƃ��ł��B
�ő�͓_�`�̂Ƃ��A�ŏ��͓_�a�̂Ƃ��ɂȂ�܂��B
���c�d�b�́A�O�ӂ�3:4:5�̒��p�O�p�`�Ȃ̂łb�c��5�A�~�@�̔��a��2�Ȃ̂ł`�c���a�c��2�ł��B
�����s��
�ő�l�́A![]()
�ŏ��l�́A![]()

�������b�c�́A�X��
![]() �ŁA�_
�ŁA�_![]() ��ʂ�̂ŁA
��ʂ�̂ŁA
![]()
����ƁA�~�@
![]() �Ƃ�A��������ƁA
�Ƃ�A��������ƁA

![]()
����āA�ő�l47�̂Ƃ�![]() �A�ŏ��l7�̂Ƃ�
�A�ŏ��l7�̂Ƃ�![]()
(2)
�����̎������Ƃ����܂��B
![]()
���͉~�@�̎���̓_�Ƃb�Ƃ����Ԓ����̌X���ł��B
����āA���̍ő�E�ŏ��́A���̒������~�@�Ɛڂ���Ƃ��ł��B
�ő�͓_�`�̂Ƃ��A�ŏ��͓_�a�̂Ƃ��ɂȂ�܂��B

�_�b��ʂ�A�X�����̒����́A![]() �B
�B
(0)�ƁA�~�@ ![]() �Ƃ�A��������ƁA
�Ƃ�A��������ƁA
![]()
![]()
���ʎ��c��0�Ƃ���ƁA
![]()
![]()
����āA�ő�l��
![]()
���_�b��ʂ�ڐ��́A


�E
![]() �Ɛ����ȌX���́A
�Ɛ����ȌX���́A![]()
![]() �Ɛ����ȌX���́A
�Ɛ����ȌX���́A![]()
�E
�X��
![]() �ŁA�_�c��ʂ钼���́A
�ŁA�_�c��ʂ钼���́A
![]()
�X��
![]() �ŁA�_�c��ʂ钼���́A
�ŁA�_�c��ʂ钼���́A
![]()
�E
(1)�A(3)��A��������ƁA

(2)�A(4)��A��������ƁA

����āA
�ő�l
![]() �̂Ƃ�
�̂Ƃ�![]() �A�ŏ��l
�A�ŏ��l ![]() �̂Ƃ�
�̂Ƃ�![]()
�� �X�����́A�_![]() �Ɛڐ��̋�����2�Ȃ̂ŁA(0)��
�Ɛڐ��̋�����2�Ȃ̂ŁA(0)��![]() �Ƃ���ƁA
�Ƃ���ƁA
![]() �Ƃ��Ă����߂��܂��B
�Ƃ��Ă����߂��܂��B
(3)
��
![]() �́A�x�N�g��
�́A�x�N�g��![]() �A
�A![]() �̓��ςł��B
�̓��ςł��B
���ς́A���ꂼ��̃x�N�g����(�傫��)��(�Ȃ��p�̗]��)�̐ςł��B
�]���́A�Ȃ��p��0�x�̂Ƃ��ő�l��1�A�Ȃ��p��180�x�̂Ƃ��ŏ��l�́|1�ł��B
�x�N�g��![]() �̑傫���͈���10�ł��B
�̑傫���͈���10�ł��B
�x�N�g��![]() �̑傫���̍ő�́A�I�_���a�̂Ƃ��ł��B(5+2��7)
�̑傫���̍ő�́A�I�_���a�̂Ƃ��ł��B(5+2��7)
�ő�l��![]() �A�ŏ��l��
�A�ŏ��l��![]()

�������`�b
![]() ���~�@�ƘA��������ƁA
���~�@�ƘA��������ƁA

�D�F�́A���_�ɋ߂����̌�_�ł��B
����āA
�ő�l70�̂Ƃ��@��̓_��![]() �A�A��̓_��
�A�A��̓_��![]() �B
�B
�ŏ��l�|70�̂Ƃ��@��̓_��![]() �A�A��̓_��
�A�A��̓_��![]() �B
�B
���2
��

�����̕���̓Ƃ̒l�ɂ�炸���̒l���Ƃ�܂��B
���q�́A

![]()
�}�̂悤�ȓ݊p�̃Ƃ̂Ƃ��A���q��0�ɂȂ�܂��B

�܂��A���łɁA
![]()
![]()
����āA�݊p�̗]���͕��Ȃ̂ŁA


��
�����́A�Ɓ�0�Ő��̒l���Ƃ�܂��B
��̐}�̂悤���݊p�̃��̂Ƃ�0�ɂȂ�܂��B
(���̃Ƃ� ![]() �Ƃ��܂�)
�Ƃ��܂�)
���̌�A���̒l���Ƃ�܂��B(�Ɓ��̂Ƃ������ł�)
�O���t�́A���悻���̐}�̂悤�ł��B

![]()
![]()

![]()
![]()
����āA�ő�l��![]() �A�ŏ��l��1�B
�A�ŏ��l��1�B
�� ![]() �̍ő�E�ŏ��́A
�̍ő�E�ŏ��́A![]() �ƍl���āA�P�ʉ~�̏㔼�����l����ƁA
�ƍl���āA�P�ʉ~�̏㔼�����l����ƁA
�_![]() �Ǝ���̓_�����Ԓ����̌X���ł��B
�Ǝ���̓_�����Ԓ����̌X���ł��B
�ŏ���1�͌��ĕ�����܂��B�ő�́A���1(2)�Ɠ��l�̍l���ŋ��߂��܂��B

���3
(1)
��
���̍���![]() �A�E�̍���
�A�E�̍���![]() �_�Ƃ���u�u�v���^�̃O���t�ɂȂ�܂��B
�_�Ƃ���u�u�v���^�̃O���t�ɂȂ�܂��B

���̐}����A�ŏ��l���Ƃ邘�́A�|2����3�̊Ԃ̂ǂ����ɂȂ�܂��B
��

�����̕���͂��̒l�ɂ�炸���̒l���Ƃ�܂��B
���q��0�ƂȂ邘�ׂ܂��B
![]()
![]()
![]()
![]() �́A�Ȃ��̕������u�|�v�̂Ƃ��̉��ł��B
�́A�Ȃ��̕������u�|�v�̂Ƃ��̉��ł��B
������0�ƂȂ�̂́A![]() �ł��B
�ł��B
|
|
���� |
|
���� |
|
|
|
|
|
|
|
���� |
|
���� |
����āA![]() �̂Ƃ��A�ŏ��l��
�̂Ƃ��A�ŏ��l��![]() �ƂȂ�܂��B
�ƂȂ�܂��B
�� ![]() �́A�_
�́A�_![]() ������
������ ![]() ��̓_�Ƃ̋����ƍl�����܂��B
��̓_�Ƃ̋����ƍl�����܂��B
![]() �́A�_
�́A�_![]() ������
������ ![]() ��̓_�Ƃ̋����ƍl�����܂��B
��̓_�Ƃ̋����ƍl�����܂��B

�ŒZ�́A�_![]() �Ɠ_
�Ɠ_![]() �Ƃ����ꍇ�ł��B
�Ƃ����ꍇ�ł��B
(2)
��
![]() �Ƃ����܂��B
�Ƃ����܂��B
��2���́A![]() �̂Ƃ��ŏ��l0���Ƃ�܂��B
�̂Ƃ��ŏ��l0���Ƃ�܂��B
��3���́A�A![]() �̂Ƃ��ŏ��l1���Ƃ�܂��B
�̂Ƃ��ŏ��l1���Ƃ�܂��B
Z�̍ŏ��l�́A![]() �͈̔͂̂Ƃ��ƍl�����܂��B
�͈̔͂̂Ƃ��ƍl�����܂��B
�E�܂��A���̕ω��ɂ��Ē��ׂ܂��B

�����̕���͐��̒l���Ƃ�܂��B
���q��0�̂Ƃ��ׂ܂��B
![]()
![]()
![]() �Ƃ���ƁA
�Ƃ���ƁA![]() �ł��B�i
�ł��B�i![]() �j
�j
![]()
![]() �͂Ȃ��̕������}�C�i�X�̂Ƃ��̉��ł��B
�͂Ȃ��̕������}�C�i�X�̂Ƃ��̉��ł��B
��
![]() �����̎��ɑ�����܂��B
�����̎��ɑ�����܂��B




�����̕���͐��̒l���Ƃ�܂��B
���q��0�̂Ƃ��ׂ܂��B
![]()
![]()
![]()
![]() �͂Ȃ��̕������}�C�i�X�̂Ƃ��̉��ł��B
�͂Ȃ��̕������}�C�i�X�̂Ƃ��̉��ł��B
�����
![]() �ɑ������ƁA
�ɑ������ƁA![]() �ƂȂ�̂ŁA
�ƂȂ�̂ŁA![]()
������A�������߂�ƁA

![]()
�ŏ��l�́A![]() �̂Ƃ�
�̂Ƃ�![]() �ł��B
�ł��B
�Q�l�܂łɒl���v�Z���Ă݂܂��B
|
|
|
|
|
|
�a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
�� �}�̂o�̍��W��![]() �Ƃ��܂��B
�Ƃ��܂��B
�o����A���ɕ��s�ȕ⏕���������A���}�̂悤�ɂp�A�q���Ƃ�܂��B
![]() �ł��B
�ł��B
�}�̂悤�ɁA![]() �ł��B
�ł��B

���ɁA�E�}�̂悤�ɑΊp���n�b�������܂��B
�n�b�ɕ��s�Ȓ������`�Ƃa��������A�p�A�q�����߂܂��B
�}�̂悤��2�g�̒��p�O�p�`�������Ȃ̂ŁA![]() �ł��B
�ł��B
![]() �Ƃ��Ē������v�Z����悢���ƂɂȂ�܂��B
�Ƃ��Ē������v�Z����悢���ƂɂȂ�܂��B
(3)
��

![]() ��̓_�o�̍��W��
��̓_�o�̍��W��![]() �Ƃ��܂��B
�Ƃ��܂��B
����0�ȏ�ł��B
![]() �Ƃ����܂��B
�Ƃ����܂��B

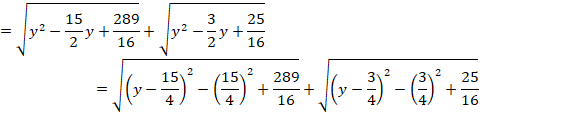


�����̕���͐��̒l���Ƃ�܂��B
���q��0�ɂȂ�Ƃ��ׂ܂��B



![]() �́A�Ȃ��̕������}�C�i�X�̂Ƃ��̉��ł��B
�́A�Ȃ��̕������}�C�i�X�̂Ƃ��̉��ł��B
|
|
|
��� |
|
���� |
|
|
|
|
|
|
|
|
|
���� |
|
���� |
����āA![]() �̂Ƃ��A�ŏ��l
�̂Ƃ��A�ŏ��l![]() ���Ƃ�܂��B
���Ƃ�܂��B
�� �o�̍��W��
![]() �Ƃ��܂��B
�Ƃ��܂��B
![]()
![]()
����āA
�o�`��
![]() ��
��![]() �Ƃ̋����Ɠ����ł��B
�Ƃ̋����Ɠ����ł��B
�o�a��
![]() ��
��![]() �Ƃ̋����Ɠ����ł��B
�Ƃ̋����Ɠ����ł��B
�����b�c�̂��ؕЂ�
![]() �Ɠ������Ȃ��
�Ɠ������Ȃ��![]() ���ŏ��ƂȂ�܂��B
���ŏ��ƂȂ�܂��B

NO5�u�O�p��K�v�@�@�@�@04/01
23��42�� ��M �X�V 4/2
��ꂽ����������
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B













