�ߘa�U�N�Q���S��
 [���ꐯ]
[���ꐯ]
�@�@��435�����w�I�ȘA�������
�@�@�@�@����W���ԁF1��7���`�Q���S����
�u��t��̉ߋ���n
�@
�lj�����i�o��҂́u�W���[�J�[�v�j
�@����2024�Ɋւ�����V���[�Y��Q�i
���P

���Q

���R

���S(��427��́u�m�����v�̖��V���[�Y�̂X���)

�@
NO1�u�W���[�J�[�v �@1/7 �@�@
18��45�� ��M �X�V 2/4
��ꂽ�����������
NO2�u�X���[�N�}���v 1/8
00��00���@ ��M �X�V 2/4
���N���ʊ��Ƀ`�������W�I�I
���P
m^4+5m^2
=m^2(m^2+5)
m^2 ��2m+1�Ƃ݂͌��ɑf
so�c
m^2+5��2m+1�̔{��
�Em=2k �̂Ƃ�
m^2+5
=(2k)^2+5=4k^2+5
2m+1=4k+1
(4k^2+5)/(4k+1)=k+(5-k)/(4k+1)
So�ck=5
�܂�Am=2*5=10
�Em=2k-1 �̂Ƃ�
m^2+5
=(2k-1)^2+5=4k^2-4k+6
2m+1
=2(2k-1)+1
=4k-1
(4k^2-4k+6)/(4k-1)
=k+(6-3k)/(4k-1)
So�ck=1,2
�܂�Am=1,3
���ǁc
m=1,3,10
�����̗���F���ɂ������͂���܂���
���Q
(21)
z^3=-i
=cos((2n+3/2)��)+i*sin((2n+3/2)��)
So�c
z=cos((4n+3)/6*��)+i*sin((4n+3)/6*��)�cn=����
(22)
���l��
z^100=-i=cos((4n+3)/2*��)+i*sin((4n+3)/2*��)
z=cos((4n+3)/200*��)+i*sin((4n+3)/200*��)
�}���
��+��/3<=(4n+3)/200*��<2�� �Ȃ炢���B
So�c
4/3<=(4n+3)/200<2
(800-9)/12<=n<(400-3)/4
791/12<=n<397/4
65.<=n<99.
So�c
66<=n<=99
So�c
99-65=34��
�W���[�J�[�l�̒lj����
���1
���ׂĂ̍���x^(11a+23b)�̌`������A
11a+23b ��11��23�Ƃ݂͌��ɑf�Ȑ��Ȃ̂�
�V����I�ɁA(11-1)(23-1)=220�ȏ�͂��ׂĕ\����B
�܂��A�������V����I�ɁA11a+23b��0〜219�܂ł̔������\����̂�
220/2+2024-220+1
=110+1805
=1915���E�E�E�s����
���Q
111�c111
=(10^2024-1)/9
�^��
=(1/3)��(10^2024-1)
(10^1012+1)(10^1012-1)
(10^1012-1/(10^1014))^2<10^2024-1<(10^1012)^2
10^2024-1/50+1/(10^2028)<10^2024-1<10^2024
(999�c999.999�c999)/3<�^��<1000�c000/3
333�c333.333�c333<�^��<333�c333.333�c
So�c3�E�E�E�ɂ�����������l����
���R
2024^2-024=x
t=��(x+��(x+��(x�c
t^2=x+t
t^2-t=2024^2-2024
so�ct=2024
���S
(97/100)^n<1/2
n*(log9.7-1)<-log2
n(1-log9.7)>log2
n>log2/(1-log9.7)=0.3010/0.0132=22.8�c
so�c23���ȏ�
�u�X���[�N�}���v 1/8
00��00���@ ��M �X�V 2/4
���P
m^4+5m^2
=m^2(m^2+5)
m^2 ��2m+1�Ƃ݂͌��ɑf
so�c
m^2+5��2m+1�̔{��
m��4�ł͂Ȃ��̂�
4m^2+20=(2m+1)^2-4m+19=(2m+1)^2-2(2m+1)+21
So�c21�̖�2m+1�ł�������B
21=3*7
2m+1=�}1,3,7,21
So�c
m=0,-1,1,-2,3,-4,10,-11
*m�͐��̐����łȂ��Ă������̂ł��� ^^;
�W���[�J�[�l�̖��2��
�}�N���[�����W�J���Ă̂͂悭�킩��Ȃ����̂�...
�]�������߂Ă݂܂���...
111�c111
=(10^2024-1)/9
�^��
=(1/3)��(10^2024-1)
so�c�ȉ��̂悤�ɕ]�����Ă݂�
(10^1012-1/(*10^1012))^2<10^2024-1<(10^1012-1/(2*10^1012))^2�E�E�E�@
10^2024-2+1/(10^2024)<10^2024-1<10^2024-1+1/(4*10^2024)
So�c�@��
999�c998.000�c001000�c<��(10^2024-1) <999�c999.000�c0005000�c
�����_1013�Ԗڂ́A���ꂼ��A���ӂ�10 ��0, �E�ӂ�05 ��5
So�c�����1/3�́c
333�c332.666�c6667000�c< <333�c333.000�c0001666�c So�c
�����_1013�Ԗڂ͍��ӂ�70 ��0�A�E�ӂ�01��1
So�c0(0)���傫��,1(6)��菬����
������ɂ���A�����_��1013�Ԗڂ�1�������肦�Ȃ��B
��������...^^; ?
NO3�ukasama�v
1/15
00��07���@��M �X�V 2/4
��ꂽ����1��ڂ�������
�ukasama�v
1/16
01��21���@��M �X�V 2/4
��ꂽ���̂Q�����������
NO4�u��x�Ђ����v 01/16
21��09���@ ��M �X�V 2/4
(�lj����̉�)
[��� 1]
(1+x^11+x^23)^(2024)��W�J�����Ƃ��̍����́C
23*(2024+1-11)=46322.(��)
a,b,r �͂�������������ŁC2��a<b, gcd(a,b)=1,r��(b-1)�Ƃ���D
(1+x^a+x^b)^r��W�J�����Ƃ��̍����� F(a,b,r) �Ƃ���D
F(a,b,r)�͎����Ōv�Z�ł���D
F(a,b,r)=(a*b-a-b+1)/2+(b*(r+2-b))+��[j=0..b-a-1]floor(b-(1+j*b)/(b-a))�D
(���ɁCb=k*a+1(k�͐�����)�̂Ƃ��ɂ́C
F(a,b,r)=F(a,k*a+1,r)=(k*a+1)*(2*r+2-k*a)/2.)
�ȉ��C���̌v�Z���̍����������D
0��n��b^r �Ȃ鐮�� n �ł����āC
n=a*x+b*y (������ x,y�� 0��x,0��y,x+y��r��������) ---(��)
�Ƃ����`�ɂ�����悤�Ȃ��̂̌��� F(a,b,r) �ł���D
(��)�̌`�ɂ����鐮�� n ���u�\���\�v�ƌĂԂ��Ƃɂ���D
(1) 0��n��(a*b-a-b) �Ȃ� n �̂����C�\���\�Ȃ��̂́C(a*b-a-b+1)/2 �ł���D
(�ؖ�)�@���̎咣�������悢�D
�uM+N=(a*b-a-b)�Ȃ�0�ȏ�̐��� M,N �ɑ��āCM,N �̂����C�ǂ��炩����݂̂�
�\���\�ł���D�v
0��n��(a*b-a-b) �Ȃ�C�ӂ�n�ɑ��āCgcd(a,b)=1���C
n=a*x+b*y
�ƂȂ�悤�Ȑ���(x,y)�����݂���D
n=a*x+b*y=a*(x-b*t)+b*(y+a*t)
�ł��邩��Cx��b�̔{���������������邱�Ƃ��\�D���������āC
n=a*X+b*Y (������ 0��X��(b-1))
�̌`�ɂ���������D���̂Ƃ��C�K�� X+Y��r �ƂȂ��Ă���D
(����X+Y>r�ƂȂ��Ă����Ƃ���CY>r-X���C
n=a*X+b*Y>a*X+b*(r-X)��-(b-a)*X+b*r��-(b-a)*(b-1)+b*r
��-(b-a)*(b-1)+b*(b-1)=a*b-a �ƂȂ��� 0��n��(a*b-a-b) �ɔ�����D)
0��n��(a*b-a-b)�Ȃ�Ƃ��Cn=a*x+b*y ���\���\�ł��邱�Ƃ́C
���� 0��x��(b-1) �̂��Ƃŕ\���\�ł��邱�ƂƓ��l�ł���C���̂Ƃ��C
(n=a*x+b*y���\���\�łȂ�)��(y<0)
�ƂȂ��Ă���D
M+N=(a*b-a-b)�Ȃ�0�ȏ�̐��� M,N�ɑ��āC
0��x,s��(b-1)�Ȃ鐮�� x,s ����� ���� y,t ��p���āC
M=a*x+b*y, N=a*s+b*t
�Ƃ�����D
M,N ���\���\�ł��邱�Ƃ́C���ꂼ�� y,t ���ł��邱�ƂƓ��l�D
M+N=(a*b-a-b)�ł��邩��C(a*x+b*y)+(a*s+b*t)=(a*b-a-b),
�܂�Cb*(y+t-a+1)=-a*(x+s+1).
gcd(a,b)=1�ł��邩��Cb��(x+s+1)�������D
1��(x+s+1)��(2*b-1)�ł��邩��C(x+s+1)=b.
����� y+t=-1��D
������ M,N �̂����C�ǂ��炩����݂̂��\���\�ł��邱�Ƃ�����C
�咣���]���D
(2)(a*b-a-b)<n��b*r-(b-a)*(b-1) �Ȃ鐮�� n �͂��ׂĕ\���\�ł���D
(�ؖ�)
�W�� {n,n-a,n-2*a,n-3*a,�c,n-(b-1)*a} �� b ��@�Ƃ����Ƃ���
���S��]�n�ƂȂ�D
����� n-x*a��0(mod b) �ƂȂ�悤�Ȑ��� x (0��x��(b-1))
����������݂���D
y=(n-x*a)/b �Ƃ���� n=a*x+b*y �ł���C
y=(n-x*a)/b>((a*b-a-b)-(b-1)*a)/b=-1 ��� y��0. ����ɁC
x+y
=x+(n-x*a)/b
=(n+(b-a)*x)/b
��(b*r-(b-a)*(b-1)+(b-a)*(b-1))/b
=r
�ł��邩��Cn�͕\���\�D
(3)b*r-(b-a)*(b-1)<n��b*r�Ȃ�n�̂����C�\���\�Ȃ��̂̌���
G(a,b,r) �Ƃ���ƁC
G(a,b,r)=��[j=0..b-a-1]floor(b-(1+j*b)/(b-a)).
(�ؖ�)
(1+x^a+x^b)^r=(1+(x^a)*(1+x^(b-a)))^r �ł��邩��C
(n���\���\)��(n=k*a+p*(b-a) (k,p��0��k��r,0��p��k�Ȃ鐮��) ).
n=b*r-(b-a)*(b-1)+t �Ƃ��Cn=k*a+p*(b-a) �Ƃ���C
t=(b-a)*(b-1)+k*a+p*(b-a)-b*r ---(��)
k=p=r�̂Ƃ��C(��)���Ct=(b-a)*(b-1)�ƂȂ�D
k=r��ۂ��Ȃ���Cp��1�������Ă䂭�D
p=r-1,r-2,r-3,�c�ɑΉ����āC
t=(b-a)*(b-1)-(b-a),(b-a)*(b-1)-2*(b-a),(b-a)*(b-1)-3*(b-a),�c��D
�����k=p=r-1�̂Ƃ�,(��)���Ct=(b-a)*(b-1)-b�ƂȂ�D
k=r-1��ۂ��Ȃ���Cp��1�������Ă䂭�D
p=r-2,r-3,r-4,�c�ɑΉ����āC
t=(b-a)*(b-1)-b-(b-a),(b-a)*(b-1)-b-2*(b-a),(b-a)-b-3*(b-a),�c��D
�ȉ��C���l�̑�����Ct�����̒l����葱�������s���D
���̂悤�ɂ��ē�����t�̒l�͂��ׂĈقȂ�D
(������(b-a)*(b-1)-s*b-u*(b-a)=(b-a)*(b-1)-S*b-U*(b-a)�Ȃ�s,u,S,U(s<S)�������
����ƁC(S-s)*b=(u-U)*(b-a). gcd(b,b-a)=1�ł��邩��C(b-a)��(S-s)�������D
�Ƃ��낪 0��s<S<(b-a) �ł��邩��(b-a)��(S-s)������邱�Ƃ͕s�\�D)
�ȏォ��C
G(a,b,r)
=1+(b-2)+��[j=1..floor(((b-a)*(b-1)-1)/b))](1+floor(((b-a)*(b-1)-j*b-1)/(b-a)))
=��[j=0..b-a-1]floor(b-(1+j*b)/(b-a))�D
���ɁC
G(a,k*a+1,r)=k*a*((k-1)*a+2)/2.
(1),(2),(3)���
F(a,b,r)
=(a*b-a-b+1)/2+(b*r-(b-a)*(b-1)-(a*b-a-b))+G(a,b,r)
=(a*b-a-b+1)/2+(b*(r+2-b))+��[j=0..b-a-1]floor(b-(1+j*b)/(b-a))�D
���ɁC
F(a,k*a+1,r)=(k*a+1)*(2*r+2-k*a)/2.
[��� 2]
��(1_(2024))�̏�����1013�ʂ̐����� 1 (��)
1_(2024)=(10^2024-1)/9 �ɒ��ӂ���D
A=(10^1014)*��(1_(2024))=(10^1014)*((10^2024-1)/9)^(1/2)�C
B=(10^2)*(10^2024-1)/3
�Ƃ����D
B��2026���̐������ł����āC��2����00,����ȊO�̌��͂��ׂ�3�D
���܂���A�̐��������̉�2����16�ł��邱�Ƃ������D
(B+17)^2-A^2=(1/9)*(2*10^2026+9*17^2-200)>0,
(B+16)^2-A^2=(1/9)*(-4*10^2026+400+9*16^2)<0.
����āC(B+16)^2<A^2<(B+17)^2.
����āC(B+16)<A<(B+17).
����āCA�̐��������̉�2����16�D
����āC��(1_(2024))�̏�����1013�ʂ̐����� 1.
[��� 3]
(�^��)=A�Ƃ����ƁC�@A^2=2024^2-2024+A.
����������āC�@A=2024(��)
[���4]
23���K�v(��)
1-(97/100)^n �� 1/2 �ƂȂ�悤�ȍŏ���n�����߂�悢�D
1-(97/100)^n �� 1/2
��1/2��(97/100)^n
��-log_10(2)��n*(log_10(97)-2)=n*(log_10(9.7)-1)
��-0.3010��n*(0.9868-1)
��ceil((-0.3010)/(0.9868-1))��n
��23��n.
NO5�u��ӂ����̂炢��������v01/22 16��13�� ��M �X�V 2/4
���1
![]() �ł��B
�ł��B
�� ![]() ���A
���A![]() ��k�{�̏ꍇ�ׂ܂��B
��k�{�̏ꍇ�ׂ܂��B
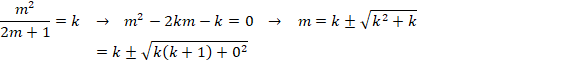
�������͘A������2�����̐ςȂ̂ŕ������ɂȂ�̂́A����0�A�|1�̂Ƃ������ł��B
����āA����0�A�|1
�� ![]() ���A
���A![]() ��k�{�̏ꍇ�ׂ܂��B
��k�{�̏ꍇ�ׂ܂��B
![]()
���������Ȃ̂ŁA�����̒��͕������ł��B
2���1��̌W�����Ƃ���1�Ȃ̂ŁA
![]()
![]()
![]()
![]()
![]()
![]()
���̐��́A![]() �Ƃ����l�ł��B
�Ƃ����l�ł��B
�T����ƁA�A������2���̐ςɂ͂Ȃ�܂���B
����2�A�|3�A5�A�|6�̂Ƃ���������̂ŁA����3�A1�A�|2�A�|4�A10�A0�A�|1�A�|11
��
�Ō�ɁA![]() ���A
���A![]() ��k�{�̏ꍇ�ׂ܂��B
��k�{�̏ꍇ�ׂ܂��B
2���{1�͊�Ȃ̂ŁA�f�����������ł��B
�f���̏ꍇ�́A��̂ǂ��炩�̏ꍇ�ɂȂ�A�������܂��Ă��܂��B
����āA2���{1���������̏ꍇ�ׂ�悢���ƂɂȂ�܂��B

�V���ɂ��͌�����܂���ł����B
�������āA
�����|11�A�|4�A�|2�A�|1�A0�A1�A3�A10
���2
�|i�̂��捪�̈�́A�K�E�X���ʂ̌��_�𒆐S�Ƃ���P�ʉ~�������̐��Ƃ����̕��̂Ȃ��p(90�x)�����������A
�����̐��̕�����1�ڂ̓_�̕��f���ł��B
���́A���̓_����ɁA�~���������������e�_�̕��f���ł��B
(1)![]() ���́A�|i��3�捪�ł��B
���́A�|i��3�捪�ł��B
�}�̐Ԃ��_�̕��f���ŁA
![]()

(2) ![]() �̉��́A����1�A2�A���100�Ƃ��āA
�̉��́A����1�A2�A���100�Ƃ��āA
![]()
�ł��B
���̕��f�������F�̕����ɓ���悢�킯�ł��B
�}�̍����̕��f���̕Ίp�́A![]() �Ȃ̂ŁA
�Ȃ̂ŁA
����67�Ƃ���ƁA�Ίp��![]() �ɂȂ�܂��B
�ɂȂ�܂��B
����āA100�|67�{1��34���ł��B

�lj����
���1
![]() �̓W�J�́A
�̓W�J�́A![]() ��
�� ![]() �����Ƃɂ��Ďw�������܂�܂��B
�����Ƃɂ��Ďw�������܂�܂��B
���̂悤�ȕ\���l���܂��B
�Ⴆ�A���̌��o����4�A��̌��o����3�̗���113�́A
![]() �Ƃ����w����\���Ă��܂��B
�Ƃ����w����\���Ă��܂��B
![]() �̓W�J�̂��̂Ƃ肤��w���͂��̕\�ɂ��ׂďo�Ă��܂��B
�̓W�J�̂��̂Ƃ肤��w���͂��̕\�ɂ��ׂďo�Ă��܂��B
��ԑ傫�Ȏw���́A![]() ��46552��ł��B
��46552��ł��B
![]() �ׂ̂��悪22�܂łȂ̂ŁA���̕\�̎w���͂��ׂĈقȂ�܂��B
�ׂ̂��悪22�܂łȂ̂ŁA���̕\�̎w���͂��ׂĈقȂ�܂��B
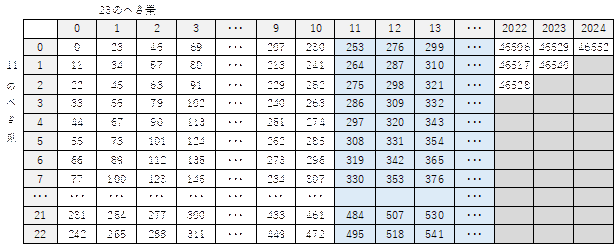
���āA![]() �ׂ̂��悪23�̗����l���Ă݂܂��B
�ׂ̂��悪23�̗����l���Ă݂܂��B
![]() �Ƃ����w���Ȃ̂ŁA����253�A����23�̓�������ł��B
�Ƃ����w���Ȃ̂ŁA����253�A����23�̓�������ł��B
����́A��̕\��11�ׂ̂��悪0�̗���23�ׂ̂��悪11�ȍ~�̒l�Ɠ����ł��B

���l�ɁA![]() �ׂ̂��悪24�̗��́A
�ׂ̂��悪24�̗��́A
![]() �Ƃ����w���Ȃ̂ŁA����264�A����23�̓�������ł��B
�Ƃ����w���Ȃ̂ŁA����264�A����23�̓�������ł��B
����́A��̕\��11�ׂ̂��悪1�̗���23�ׂ̂��悪11�ȍ~�̒l�Ɠ����ł��B
���
![]() �ׂ̂��悪45�̗��́A
�ׂ̂��悪45�̗��́A
![]() �Ƃ����w���Ȃ̂ŁA����495�A����23�̓�������ł��B
�Ƃ����w���Ȃ̂ŁA����495�A����23�̓�������ł��B
����́A��̕\��11�ׂ̂��悪22�̗���23�ׂ̂��悪11�ȍ~�̒l�Ɠ����ł��B
![]() �ׂ̂��悪46�̗��́A
�ׂ̂��悪46�̗��́A
![]() �Ƃ����w���ł��B
�Ƃ����w���ł��B
����́A��̕\��11�ׂ̂��悪0�̗���23�ׂ̂��悪22�ȍ~�̒l�Ɠ����ł��B
���
![]() �ׂ̂��悪68�̗��́A
�ׂ̂��悪68�̗��́A
![]() �Ƃ����w���ł��B
�Ƃ����w���ł��B
����́A��̕\��11�ׂ̂��悪22�̗���23�ׂ̂��悪22�ȍ~�̒l�Ɠ����ł��B
���̂悤�ɁA23�s���Ƃɍŏ��̕\�̓r�����瓯����������܂��B
����āA�ŏ��̕\�̐��̌������߂铚���ɂȂ�܂��B
�ŏ��̕\��11�ׂ̂��悪22�̗��́A�s��1������ƁA1�}�X����̂ŁA2003����̂ŁA
![]()
���2
�Ȃ�邽�߂ɁA![]() �̏�����3�ʂׂ܂��B
�̏�����3�ʂׂ܂��B
���̂��߂ɁA![]() ���g���܂��B
���g���܂��B
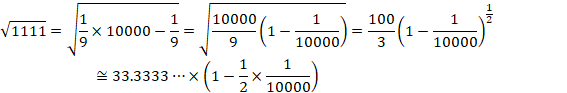
![]()
![]()
����ɏK���A���������܂��B

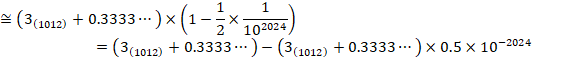
![]()
����āA������1013�ʂ́A1�B
���3
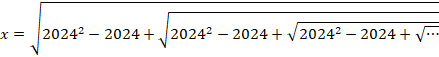 �Ƃ����܂��B
�Ƃ����܂��B
���ӂ�2�悵�܂��B
 �ł��B
�ł��B
�䂦�ɁA
![]()
![]()
���4
3����������m���� ![]() �ȏ�ɂ���ƌ������Ƃ́A
�ȏ�ɂ���ƌ������Ƃ́A
3����������Ȃ��m���� ![]() ��菬�����ɂ���ƌ������Ƃł��B
��菬�����ɂ���ƌ������Ƃł��B
�͂���1���ɂ��āA3����������Ȃ��m���́A![]() �Ȃ̂ŁA�͂����������Ƃ���ƁA
�Ȃ̂ŁA�͂����������Ƃ���ƁA

![]()
![]()
����āA�͂���23���͕K�v�B
�u�O�p��K�v�@�@�@�@02/03
17��35���@ ��M �X�V 2/4
��ꂽ�����������
�u���̗���v
�X�V 2/4
 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@

�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���, �ƃy���l�[����Y����, ���[���ő����Ă��������B�҂��Ă��܂��B
