令和６年３月３日

[流れ星]

　　第436回数学的な連続応募解答

　　　　＜解答募集期間：２月４日〜３月３日＞

「相加平均・相乗平均］

　

追加問題（出題者は「ジョーカー」）

　今回から2024に関する問題シリーズ第３段

問題１

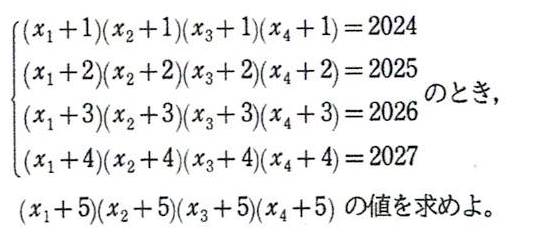
問題２

問題３　２つの有理数の3乗和が６となる問題

(第427回からの「確率等」の問題シリーズはお休みします)

NO1「ジョーカー」 　2/4 　　 20時30分 受信 更新 3/3

寄せられた問題の解答です

NO2「スモークマン」 2/5 21時01分　 受信 更新 3/3

問題

(1)

x^2+1/x

=x^2+1/(2x)+1/(2x)

>=3*(1/2)^(2/3)

等号はx^2=1/(2x)…2x^3=1…x=(1/2)^(1/3) のとき、Min=3*(1/2)^(2/3)

(2)

x^3+1/(3x)+1/(3x)+1/(3x)

>=4(1/3)^(3/4)

等号は x^3=1/(3x)…x=(1/3)^(1/4) のとき、Min=4*(1/3)^(3/4)

(3)

(1/2)(x+y)+2/(x+y)+x/2+y/2+1/(2xy)

>=2+3/2=7/2

等号は(x+y)/2=2/(x+y) かつ x/2=y/2=1/(2xy)…xy/4=1/(4(xy)^2)…xy=1

So…x+y=2,xy=1…x=y=1 のとき

Min=7/2

(4)コーシー・シュワルツの不等式で

(x+y+z)=((√x)^2+(√y)^2+(√z)^2)((1/√x)^2+(2/√y)^2+(3/√z)^2)

>=(1+2+3)^2

x:y:z=1:2:3

x=1/6,y=1/3,z=1/2

6+12+18=36

Min=36

問題1

f(x)=(x1+x)(x2+x)(x3+x)(x4+x)

x1x2x3x4=X, x1x2x3+…+x2x3x4=Y, x1x2+…+x3x4=Z, x1+x2+x3+x4=W

と置くと

f(1)=X+Y+Z+W+1=2024

f(2)=X+2Y+4Z+8W+16=2025

f(3)=X+3Y+9Z+27W+81=2026

f(4)=X+4Y+16Z+64W+256=2027

より

X=2047, Y=-49, Z=35, W=-10

So…

f(5)=X+5Y+25Z+125W+625=2047+5*(-49)+25*35+125*(-10)+625=2052

問題2

under consideration...

問題3

(x+y)(x^2-xy+y^2)

=(x+y)((x+y)^2-3xy)

x+y=2

4-3xy=3…xy=1/3

(x+y)^2-4xy=4-4/3=8/3

(x-y)^2=8/3

x+y=2

x-y=2√2/√3

x=1+√2/√3=1+√6/3

y=1-√6/3

実際に、

(1+√6/3)^3+(1-√6/3)^3

=1+2*(6/3)+1

=6

＜水の流れ：問題文のｘ、ｙは有理数です。ｘ、ｙが無理数なら正解です＞

NO3「よふかしのつらいおじさん」 2/9 21時13分 受信 更新 3/3

寄せられた問題の解答です

NO4「kasama」 2/10 　01時59分　　 受信 更新 ３/３

寄せられた問題の1回目の解答です

NO5「二度漬け白菜」 2/10 　18時07分　　受信 更新 ３/３

(追加問題の解答)

[問題 1]

求める値は，2052(答)

tについての4次の整式F(t)を次のように決める．

F(t)=(t+1+x_1)*(t+1+x_2)*(t+1+x_3)*(t+1+x_4).

問題文で与えられた4つの条件式は次のようにかける．

F(0)=2024,

F(1)=2025,

F(2)=2026,

F(3)=2027.

以上の条件のもとに，F(4)の値を求めればよい．

F(t)は最高次の係数が1であるような4次の整式であるから，

F(t)=t*(t-1)*(t-2)*(t-3)+a*t*(t-1)*(t-2)+b*t*(t-1)+c*t+d

とおける．

F(0)=2024,F(1)=2025,F(2)=2026,F(3)=2027 であるから，

d=2024,c=1,b=0,a=0 であることが判る．

すなわち，

F(t)=t*(t-1)*(t-2)*(t-3)+t+2024.

よって，

F(4)=4!+4+2024=2052.(答)

[問題 2]

(与式)=2023 (答)

α=(2023/2024) とおく．

(2023^k)*(2024^k)/((2024^k-2023^k)*(2024^(k+1)-2023^(k+1)))

=1/(1-α^k) - 1/(1-α^(k+1))

である． よって，

(与式)

=Σ[k=1〜∞](1/(1-α^k) - 1/(1-α^(k+1)))

=lim[N→∞]Σ[k=1〜N](1/(1-α^k) - 1/(1-α^(k+1)))

=lim[N→∞](1/(1-α) - 1/(1-α^(N+1)))

=1/(1-α) - 1

=2024-1

=2023.

[問題 3]

x^3+y^3=6を満たす有理数の組(x,y)の一つは，

(x, y)=(17/21, 37/21) (答)

上記以外の組としては，

(x, y)=(2237723/960540, -1805723/960540),

(x, y)=(209143555850753/112490043311709, -84691068680987/112490043311709),

(x, y)=(29835171298114433945011441/16418498901144294337512360, -1276454530530789553459441/16418498901144294337512360)

などがある．

この[問題3]に関して，次のような興味深い記事を見つけました．

https://www.jstor.org/stable/2691526

「A^3/B^3 + C^3/D^3 = 6 を満たすような100未満の正整数

A,B,C,Dを見つけなさい．さらに100を超えるようなものは

果たして存在するのか？」という問題に，450ポンドの賞金

が懸けられていたようです．

＜水の流れ：情報ありがとうございます。＞

NO5「日曜数学者」 2/17 　21時36分　　受信 更新 ３/３

*追加問題の問題１の解答です。

*

*連立代数方程式の解を求めることは、複数の多項式の共通の霊点を求めることと同値なので、*

*その多項式系のGroebner基底を計算すると簡単に解けることが多いです。*

*

(x1+1)*(x2+1)*(x3+1)*(x4+1)=2024,

(x1+2)*(x2+2)*(x3+2)*(x4+2)=2025,

(x1+3)*(x2+3)*(x3+3)*(x4+3)=2026,

(x1+4)*(x2+4)*(x3+4)*(x4+4)=2027,

(x1+5)*(x2+5)*(x3+5)*(x4+5)=c

とする。

Asir2000によって、多項式環Q[x1,x2,x3,x4,c]上で、

[(x1+1)*(x2+1)*(x3+1)*(x4+1)-2024, (x1+2)*(x2+2)*(x3+2)*(x4+2)-2025, (x1+3)*(x2+3)*(x3+3)*(x4+3)-2026, (x1+4)*(x2+4)*(x3+4)*(x4+4)-2027, (x1+5)*(x2+5)*(x3+5)*(x4+5)-c]

のGroebner基底を求めると、

[c-2052,-x1-x2-x3-x4-10,x2^2+(x3+x4+10)*x2+x3^2+(x4+10)*x3+x4^2+10*x4+35,

 x3^3+(x4+10)*x3^2+(x4^2+10*x4+35)*x3+x4^3+10*x4^2+35*x4+49,

 x4^4+10*x4^3+35*x4^2+49*x4+2047]

となる。

よって、c-2052=0 つまり c=2052である。

[Asir2000による計算結果]

This is Risa/Asir, full GMP Version 20200109 (Kobe Distribution).

Copyright (C) 1994-2000, all rights reserved, FUJITSU LABORATORIES LIMITED.

Copyright 2000-2019, Risa/Asir committers, http://www.openxm.org/.

GC 7.4.2 copyright 1988-2015, H-J. Boehm, A. J. Demers, Xerox, SGI, HP.

[0] load("gr");

[107] F1=(x1+1)*(x2+1)*(x3+1)*(x4+1)-2024;

(((x4+1)*x3+x4+1)*x2+(x4+1)*x3+x4+1)*x1+((x4+1)*x3+x4+1)*x2+(x4+1)*x3+x4-2023

[108] F2=(x1+2)*(x2+2)*(x3+2)*(x4+2)-2025;

(((x4+2)*x3+2*x4+4)*x2+(2*x4+4)*x3+4*x4+8)*x1+((2*x4+4)*x3+4*x4+8)*x2+(4*x4+8)*x3+8*x4-2009

[109] F3=(x1+3)*(x2+3)*(x3+3)*(x4+3)-2026;

(((x4+3)*x3+3*x4+9)*x2+(3*x4+9)*x3+9*x4+27)*x1+((3*x4+9)*x3+9*x4+27)*x2+(9*x4+27)*x3+27*x4-1945

[110] F4=(x1+4)*(x2+4)*(x3+4)*(x4+4)-2027;

(((x4+4)*x3+4*x4+16)*x2+(4*x4+16)*x3+16*x4+64)*x1+((4*x4+16)*x3+16*x4+64)*x2+(16*x4+64)*x3+64*x4-1771

[111] F5=(x1+5)*(x2+5)*(x3+5)*(x4+5)-c;

-c+(((x4+5)*x3+5*x4+25)*x2+(5*x4+25)*x3+25*x4+125)*x1+((5*x4+25)*x3+25*x

-c+4+125)*x2+(25*x4+125)*x3+125*x4+625

[112] gr([F1,F2,F3,F4,F5],[x1,x2,x3,x4,c],0);

[c-2052,-x1-x2-x3-x4-10,x2^2+(x3+x4+10)*x2+x3^2+(x4+10)*x3+x4^2+10*x4+35,x3^3+(x4+10)*x3^2+(x4^2+10*x4+35)*x3+x4^3+10*x4^2+35*x4+49,x4^4+10*x4^3+35*x4^2+4

9*x4+2047]

[113]quit;

--------------------------------------------------

*おまけ(一般化)です。*

*2024,2025,2026,2027を定数a,b,c,dで置き換えて、

*

*(x1+1)*(x2+1)*(x3+1)*(x4+1)=a,

(x1+2)*(x2+2)*(x3+2)*(x4+2)=b,

(x1+3)*(x2+3)*(x3+3)*(x4+3)=c,

(x1+4)*(x2+4)*(x3+4)*(x4+4)=d,

(x1+5)*(x2+5)*(x3+5)*(x4+5)=e

とするとき、eを求める。

Asir2000によって、多項式環Q[x1,x2,x3,x4,e]上で、

[(x1+1)*(x2+1)*(x3+1)*(x4+1)-a, (x1+2)*(x2+2)*(x3+2)*(x4+2)-b,

 (x1+3)*(x2+3)*(x3+3)*(x4+3)-c, (x1+4)*(x2+4)*(x3+4)*(x4+4)-d,

 (x1+5)*(x2+5)*(x3+5)*(x4+5)-e]

のGroebner基底を求めると、

[a-4*b+6*c-4*d+e-24,

-a+3*b-3*c+d-6*x1-6*x2-6*x3-6*x4-60,

 (x2+x3+x4+9)*a+(-3*x2-3*x3-3*x4-24)*b+(3*x2+3*x3+3*x4+21)*c+(-x2-x3-x4-6)*d+6*x2^2+(6*x3+6*x4+60)*x2+6*x3^2+(6*x4+60)*x3+6*x4^2+60*x4+210,

(x3^2+(x4+9)*x3+x4^2+9*x4+26)*a+(-3*x3^2+(-3*x4-24)*x3-3*x4^2-24*x4-57)*b+(3*x3^2+(3*x4+21)*x3+3*x4^2+21*x4+42)*c+(-x3^2+(-x4-6)*x3-x4^2-6*x4-11)*d+6*x3^3+(6*x4+60)*x3^2+(6*x4^2+60*x4+210)*x3+6*x4^3+60*x4^2+210*x4+300,

(x4^3+9*x4^2+26*x4+24)*a+(-3*x4^3-24*x4^2-57*x4-36)*b+(3*x4^3+21*x4^2+42*x4+24)*c+(-x4^3-6*x4^2-11*x4-6)*d+6*x4^4+60*x4^3+210*x4^2+300*x4+144]

となる。

よって、a-4*b+6*c-4*d+e-24=0 より、

   e=-a+4*b-6*c+4*d+24

である。

[Asir2000による計算結果]

This is Risa/Asir, full GMP Version 20200109 (Kobe Distribution).

Copyright (C) 1994-2000, all rights reserved, FUJITSU LABORATORIES LIMITED.

Copyright 2000-2019, Risa/Asir committers, http://www.openxm.org/.

GC 7.4.2 copyright 1988-2015, H-J. Boehm, A. J. Demers, Xerox, SGI, HP.

[0] load("gr");

[107] F1=(x1+1)*(x2+1)*(x3+1)*(x4+1)-a;

-a+(((x4+1)*x3+x4+1)*x2+(x4+1)*x3+x4+1)*x1+((x4+1)*x3+x4+1)*x2+(x4+1)*x3

-a++x4+1

[108] F2=(x1+2)*(x2+2)*(x3+2)*(x4+2)-b;

-b+(((x4+2)*x3+2*x4+4)*x2+(2*x4+4)*x3+4*x4+8)*x1+((2*x4+4)*x3+4*x4+8)*x2

-b++(4*x4+8)*x3+8*x4+16

[109] F3=(x1+3)*(x2+3)*(x3+3)*(x4+3)-c;

-c+(((x4+3)*x3+3*x4+9)*x2+(3*x4+9)*x3+9*x4+27)*x1+((3*x4+9)*x3+9*x4+27)*

-c+x2+(9*x4+27)*x3+27*x4+81

[110] F4=(x1+4)*(x2+4)*(x3+4)*(x4+4)-d;

-d+(((x4+4)*x3+4*x4+16)*x2+(4*x4+16)*x3+16*x4+64)*x1+((4*x4+16)*x3+16*x4

-d++64)*x2+(16*x4+64)*x3+64*x4+256

[111] F5=(x1+5)*(x2+5)*(x3+5)*(x4+5)-e;

-e+(((x4+5)*x3+5*x4+25)*x2+(5*x4+25)*x3+25*x4+125)*x1+((5*x4+25)*x3+25*x

-e+4+125)*x2+(25*x4+125)*x3+125*x4+625

[112] gr([F1,F2,F3,F4,F5],[x1,x2,x3,x4,e],0);

[a-4*b+6*c-4*d+e-24,-a+3*b-3*c+d-6*x1-6*x2-6*x3-6*x4-60,(x2+x3+x4+9)*a+(-3*x2-3*x3-3*x4-24)*b+(3*x2+3*x3+3*x4+21)*c+(-x2-x3-x4-6)*d+6*x2^2+(6*x3+6*x4+60)*

x2+6*x3^2+(6*x4+60)*x3+6*x4^2+60*x4+210,(x3^2+(x4+9)*x3+x4^2+9*x4+26)*a+

x2+(-3*x3^2+(-3*x4-24)*x3-3*x4^2-24*x4-57)*b+(3*x3^2+(3*x4+21)*x3+3*x4^2

x2++21*x4+42)*c+

(-x3^2+(-x4-6)*x3-x4^2-6*x4-11)*d+6*x3^3+(6*x4+60)*x3^2+(6*x4^2+60*x4+210)*x3+6*x4^3+60*x4^2+210*x4+300,(x4^3+9*x4^2+26*x4+24)*a+(-3*x4^3-24*x4^2-57*x4-36

)*b+(3*x4^3+21*x4^2+42*x4+24)*c+(-x4^3-6*x4^2-11*x4-6)*d+6*x4^4+60*x4^3+210*x4^2+300*x4+144]

[113] quit;

==============================

*追加問題の問題３の解答です。

*

*x^3+y^3=6の有理数解(x,y)で最も簡単なものは、*

*  (37/21,17/21), (17/21,37/21)*

*である。*

*有理数解(楕円曲線の有理点)の一般的な求め方は、以下のURLを参照ください。*

*http://www.kaynet.or.jp/~kay/misc/nna2.html*

NO6「日曜数学者」 2/25 　16時21分　　 受信 更新 3/15

＜水の流れ：英語の投稿は初めてです。大学4年時、ゼミのテキスト以来でして翻訳に試みました。なぜか学生気分になり懐かしい。＞

NO6「三角定規」　　　　02/22 16時04分　 受信 更新 3/3

寄せられた問題の1回目の解答です

「水の流れ」 更新 ３/３

皆さん、問題や質問に答えてください。一部でも構いませんから, 解答とペンネームを添えて, メールで送ってください。待っています。