令和６年４月１４日

[流れ星]

　　第439回数学的な連続応募解答

　　　　＜解答募集期間：３月17日〜４月14日＞

「対称式・媒介変数］

追加問題（出題者は「ジョーカー」）

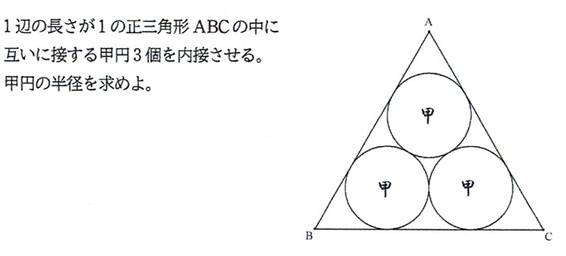
新シリーズ（正三角形の辺や円弧によって囲まれる図形内の3円の半径について）1問目

問題1

　

問題２　(第427回からの「確率等」の問題シリーズの10問目)

NO1「ジョーカー」 　 3/18 　　 5時58分 受信 更新 4/14

　寄せられた問題の解答です

NO2「スモークマン」 3/19 17時11分　 受信 更新 4/14

No 439

追加問題２

2枚目は1/13で、3枚目は2/13で…

1/13+2/13+3/13+4/13+…

=n(n+1)/26>=1

n(n+1)>=26

4*5<26<5*6

So…5+1=6枚が期待値

鳩の巣からだと…7枚で必ず1ペアにできるけど…

これは、最悪の場合だから、実際は…

それより1枚少ない枚数で、揃う可能性があるということなのねぇ…^^

「スモークマン」 3/24 19時02分　 受信 更新 4/14

追加問題１

甲円の半径=r とすると

正三角形ABC

=1辺が2rの正三角形4個+(r*2r)の長方形3個

=4r^2*√3+6r^2

=r^2*(4√3+6)

=√3/4・・・これを解くと...

r=(√3-1)/4

(2)

1枚目は任意

2枚目は1/13で、3枚目は2/13で…

1/13+2/13+3/13+4/13+…

=n(n+1)/26>=1

n(n+1)>=26

4*5<26<5*6

So…5+1=6枚

So…1/13+5*6/13=31/13

ということになるのでしょうかしらん ^^;

問題１

問題２

NO3「kasama」 3/25 08時23分　　 受信 更新 4/14

　寄せられた解答です

NO4「よふかしのつらいおじさん」 4/03 　11時22分 受信 更新 4/14

寄せられた解答です

NO5「三角定規」　　　　4/7 9時42分　 受信 更新 4/14

寄せられた解答です

NO6「二度漬け白菜」 4/9 11時01分　 受信 更新 4/14

第439回の追加問題2を考えてみました．

[問題文]

ある本屋さんで次のようなキャンペーンが行われた．

本を1冊買うたびにトランプのしおりが付いてくる．

そして1ペアがそろえば記念品がもらえるという．

ジョーカーはなく，同じカード2枚でも1ペアとみなす．

記念品をもらうために買う本の期待値を求めよ．

(解答)

求める期待値は，121437725363954/23298085122481 (答)

記念品をもらうまでに買った本の冊数を X とすると，

Xの期待値 E(x) は，

E(x)

=Σ[k=1..∞]k*P(X=k)

=Σ[k=1..∞](Σ[j=1..k]1)*P(X=k)

=Σ[j=1..∞]Σ[k=j..∞]P(X=k)

=Σ[j=1..∞]P(X≧j)

=Σ[j=0..∞]P(X＞j)

=Σ[j=0..∞](j!)*[t^j](1+4*(t/52))^(13)

=Σ[j=0..13](j!)*binomial(13,j)*(4/52)^j

=121437725363954/23298085122481.

( [t^j](1+4*(t/52))^(13) は，(1+4*(t/52))^(13)の

t^jの係数の意味です．)

この問題の「同じカード2枚でも1ペアとみなす」

という条件の部分を，

「同じカード2枚の場合は1ペアとはみなさない」

という条件に書き換えた場合には，記念品をもらうために

買う本の冊数 X の期待値E(X)は次のようになりました．

E(x)

=Σ[k=1..∞]k*P(X=k)

=Σ[k=1..∞](Σ[j=1..k]1)*P(X=k)

=Σ[j=1..∞]Σ[k=j..∞]P(X=k)

=Σ[j=1..∞]P(X≧j)

=Σ[j=0..∞]P(X＞j)

=Σ[j=0..∞](j!)*[t^j](1+4*(exp(t/52)-1))^(13)

=Σ[j=0..∞](j!)*[t^j](4*exp(t/52)-3)^(13)

=∫_[t=0..∞](exp(-t)*(4*exp(t/52)-3)^(13))dt

=717950116213/119065042425.

元の問題に比べて，期待値は約 0.8 上がります．

「水の流れ」　　　　　　　　　　　　　　　　　受信 更新 4/14