令和６年10月13日
[流れ星]
第446回数学的な連続応募解答
＜解答募集期間：9月15日〜10月13日＞
［図形と式］
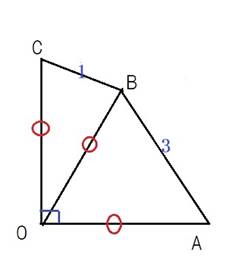
問題１
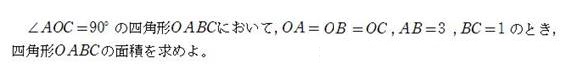
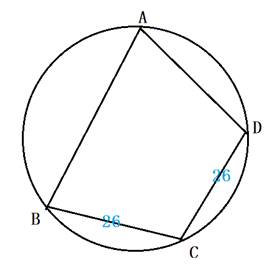
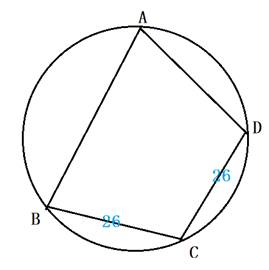
問題２ 東京大学入試問題の類題
（代々木ゼミナール最高難度の理系数学 荻野暢也 著）
追加問題（出題者は「ジョーカー」）
新シリーズ（正三角形の辺や円弧によって囲まれる図形内の４個の甲円の半径について）４,５問目で終了
問題1
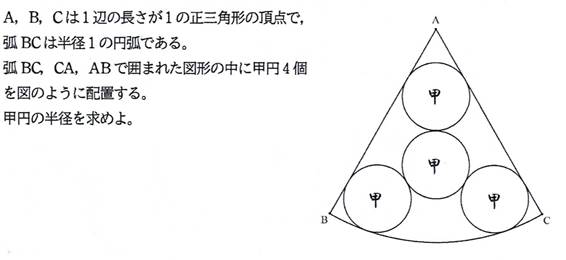
問題２
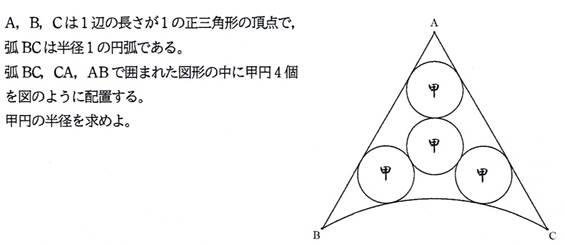
NO1「スモークマン」 9/15 15時01分 受信 更新 10/13
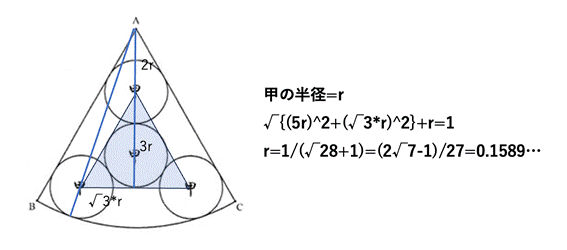
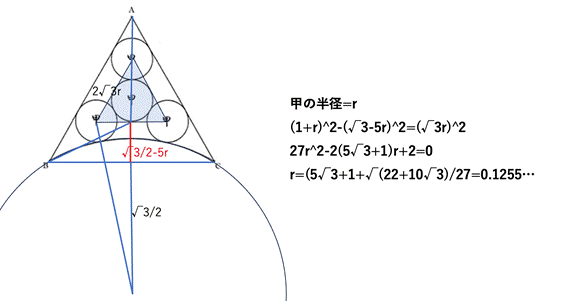
「スモークマン」 9/15 22時01分 受信 更新 10/13
問題１
2x^2(1-cosα)=3^2
2x^2(1-cos(90-α))=2x^2(1-sinα)=1
(1-9/2y)^2+(1-1/2y)^2=1
y=x^2=5±3√2/2
cos(α)=(27√2-8)/82・・・x^2=5+3√2/2
x^2=5-3√2/2 のときは cos(α)<0 で不適
sin(α)=(3/82)(24+√2)
x^2*(sin(α)+cos(α))/2
=(5+3√2/2)*( (27√2-8)/82+(3/82)(24+√2))/2
=(5+3√2/2)*(32+15√2)/41
=(5+3√2)/2
問題２ 東京大学入試問題の類題
（代々木ゼミナール最高難度の理系数学 荻野暢也 著）
88-2*26=36
AB=x,AD=y
x^2+y^2-2x*y*cosA=2*26^2*(1+cosA)=BD^2
2*(65/4)^2*(1-cosA)=26^2
cosA=-7/25
2*26^2*(1-7/25)= 24336/25
x+y=36
x^2+(36-x)^2+2x(36-x)(7/25)= 24336/25
x^2-36x+224=0
(x-8)(x-28)=0
so…
(AB,AD)=( 8,28) or (28,8)
NO2「ジョーカー」 9/15 17時25分 受信 更新 10/13
寄せられた解答です
NO3「kasama」
9/24 00時41分
受信 更新 10/13
寄せられた解答です
NO4「よふかしのつらいおじさん」9/28 21時31分 受信
更新 10/13
寄せられた解答です
N5「二度漬け白菜」 10/05 10時00分
受信 更新 10/13
第446回数学的な応募問題の解答：
[問題1]
四角形OABCの面積は，(5+3*√2)/2 (答)
以下では，△ABCの面積を[△ABC]というように表すことにする．
線分BAの中点をM，
線分BCの中点をN
とおく．
このとき，∠MON=45°である．
(∵∠MON = ∠BOM + ∠BON = (1/2)*∠BOA
+ (1/2)*∠BOC =(1/2)*(∠BOA + ∠BOC ) = (1/2)*∠AOC = 45°)
よって，∠MBN=360°-(45°+90°+90°)=135°.
△ABCに余弦定理を使って,
AC^2=3^2+1^2-2*3*1*cos(135°)=10+3*√2.
△AOCは∠AOC=90°の直角二等辺三角形であるから，
AO^2=(1/2)*AC^2.
[△AOC]=(1/2)*AO^2=(1/4)*AC^2=(10+3*√2)/4.
[△ABC]=(1/2)*3*1*sin(135°)=(3*√2)/4.
よって，
[四角形OABC]
=[△AOC]+[△ABC]
=(10+3*√2)/4 + (3*√2)/4
=(5+3*√2)/2.
[問題2]
AB=8,DA=28
または AB=28,DA=8 (答)
AB=x，r=65/4，四角形ABCDの外接円の中心を O，
∠OCB=θ とおく．
DA=36-x, cos(θ)=(26/2)/r=4/5
である．
△BCDに余弦定理を使って，
BD^2
=26^2+26^2-2*26*26*cos(2*θ)
=2*26^2*(1-cos(2*θ))
=4*26^2*(1-(cos(θ))^2)
=(2*26*(3/5))^2 ---(1)
△ABDに余弦定理を使って，
BD^2
=x^2+(36-x)^2-2*x*(36-x)*cos(180°-2*θ)
=x^2+(36-x)^2+2*x*(36-x)*cos(2*θ)
=x^2+(36-x)^2+2*x*(36-x)*(2*(cos(θ))^2-1)
=x^2+(36-x)^2+2*x*(36-x)*(2*(4/5)^2-1)
---(2)
(1),(2)より，
(2*26*(3/5))^2=x^2+(36-x)^2+2*x*(36-x)*(2*(4/5)^2-1).
これを解いて，x=8 or 28.
[追加問題1]
甲円の半径は，(-1+2*√7)/27 (答)
甲円の半径をrとする．
xy直交座標を設定して考える．
A(0,0),
B((1/2)*√3,-1/2),
C((1/2)*√3,1/2)
となるように座標を設定する．
その中心が点Aに最も近い甲円をD，
その中心が点Bに最も近い甲円をE，
甲円Dに接する甲円をF
とする．
円Dの中心Dの座標は，D(2*r,0).
円Fの中心Fの座標は，F(4*r,0).
y軸に平行で，かつ，円Fに接するような直線は2本ある．
この2本の直線のうち，点Aとの距離が大きいほうの直線を
Lとする．Lと直線AB,直線ACとの交点をそれぞれ，B',C'
とする．三角形AB'C'は正三角形である．
図形の対称性により，点F(4*r,0)は三角形AB'C'の重心であり，
∠DFE=120°，FE=FD=2*r.
これらより，Eの座標は，E(5*r,(-√3)*r).
AE=1-rが成り立つことから，28*r^2=(1-r)^2.
これを解いて，r=(-1+2*√7)/27.
[追加問題2]
甲円の半径は，(-(22+10*3^(1/2))^(1/2)+(1+5*3^(1/2)))/27 (答)
甲円の半径をrとする．
[追加問題1]と同じようにxy直交座標を設定して考え，
点A,B,C,D,E,Fの定義も同様にする．
G(√3,0)とする．
GE=1+rが成り立つことから，(5*r-√3)^2+((-√3)*r)^2=(1+r)^2.
これを解いて，r=(-(22+10*3^(1/2))^(1/2)+(1+5*3^(1/2)))/27.
(以上)
NO6「三角定規」
10/05
22時02分 受信 更新 10/13
寄せられた解答です
＜コメント：私の解法はやや複雑な三角方程式を解くもので,
きたない無理数を覚悟したのですが，結果はすべてきれいな有理数。
東大入試の類題だそうですが，こんなきれいな数の関係,
発見者はかなりの試行錯誤を繰り返したことでしょうね！ 脱帽です。＞
＜水の流れ：出題した図形に関係から、AB=８,AD＝２８も答になります。＞
＜水の流れ＞ 問題１
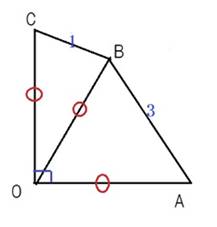
問題２
皆さん、問題や質問に答えてください。一部でも構いませんから, 解答とペンネームを添えて, メールで送ってください。待っています。
