令和６年11月10日

[流れ星]

　　第447回数学的な連続応募解答

　　　＜解答募集期間：10月13日〜11月10日＞

「雑題３問］

問題１　1978年　群馬大学入試問題　

BLUE　BACKS入試問題伝説の良問100　安田亨著

問題２　電卓を利用すると答えはでるよ。

問題３　

追加問題（出題者は「ジョーカー」）　新作シリーズ１,２問目

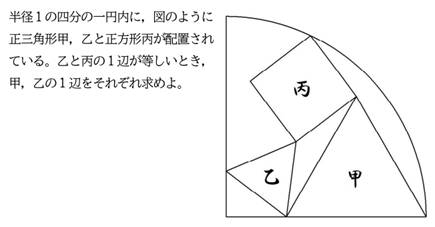
問題1

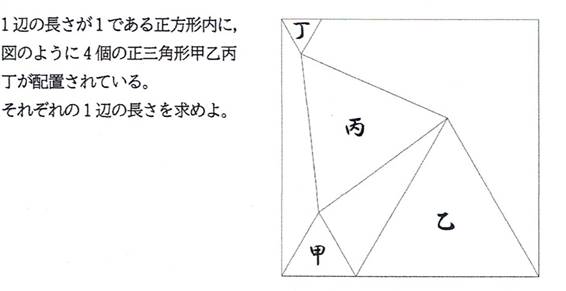
問題２

　

NO1「ジョーカー」 　10/13 　13時21分 受信 更新 11/10

寄せられた解答です

NO2「スモークマン」 10/20 15時31分　 受信 更新 11/10

問題２　電卓を利用すると答えはでるよ。

(m+0.02)^2<n^2+1<(m+0.03)^2

m^2+0.04*m<n^2+1<=m^2+0.06*m

0.04*m<1<0.06*m

16<m<25

so…

17<=n<=24

「スモークマン」 10/20 18時49分　 受信 更新 11/10

追加問題２

「スモークマン」 10/20 21時26分　 受信 更新 11/10

問題１　

10^3*a+10^2*b+10*c+d=(10(a+c)+(b+d))^2

a+c=x,b+d=y

10^3*a+10^2*b+10*(x-a)+y-b=(10x+y)^2

990*a+99b=(10x+y)(10x+y-1)・・・右辺は互いに素

99(10a+b)=(10x+y)(10x+y-1)

10x+yと10x+y-1との差は1なので、片方が1になることはない

So…以下の4つの場合を考えればいい。

(1)10x+y=99…10a+b=98…a=9,b=8,c=0,d=1

(2)10x+y-1=99 のとき、10x+y=100 はありえない

(3)10x+y=11k,10x+y-1=11k-1=9m

11-10, 22-21,33-32,44-43,55-54,66-65,77-76,88-87,99-98

x=y=5…55^2=3025

(4)10x+y=9k, 10x+y-1=9k-1=11m

18-17,27-26,36-35,45-44,54-53,63-62,72-71,81-80,90-89,99-98

x=4,y=5…45^2=2025

求とめる4桁は、9801,3025,2025 の3つ

問題３　

100(x+y)=xy

(100-y)x-100(100-y)=-10000

(x-100)(y-100)=10000=2^4*5^4

x=y=200 以外は、

5^2-1=24・・・12ペア

(x-100)+(y-100)=x+y-200

So…この約数の和=(1+2+2^2+2^3+2^4)(1+5+5^2+5^3+5^4)・・・ここ間違ってました ^^;

=(2^5-1)(5^5-1)/4

=24211

So…

24211-100=24111

So…24111+200*12=26511

So…

求めるものは

26511+2*200=26911

「スモークマン」 10/27 15時00分　 受信 更新 11/10

追加問題１

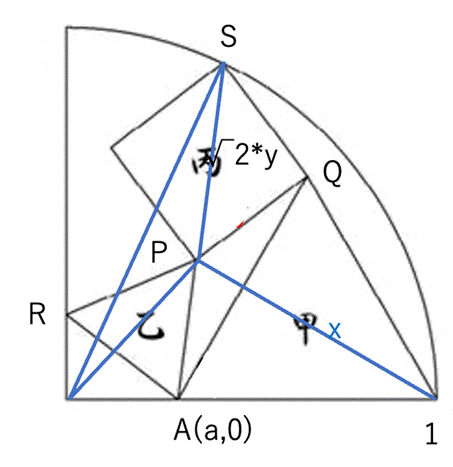
P(p,√3(1-p)/3)

A(a,0)

Q=((1+a)/2,(√3/2)(1-a))

(PQ)=((1+a)/2-p,(√3/2)(1-a)-√3(1-p)/3)

S=P+(PQ)*(1+i)

=P+((1+a)/2-p- ((√3/2)(1-a)-√3(1-p)/3), (1+a)/2-p+ ((√3/2)(1-a)-√3(1-p)/3)

=(((1+a)/2- ((√3/2)(1-a)-√3(1-p)/3), (1+a)/2-p+ ((√3/2)(1-a)) So… (((1+a)/2-(√3/2)(1-a)+√3(1-p)/3))^2+ ((1+a)/2-p+(√3/2)(1-a))^2=1

A+PA*(1/2,√3/2) のx座標=0

So…

(a,0)+(p-a,√3(1-p)/3)(1/2,√3/2)

a+(p-a)/2-(1-p)/2=0

(a,p)=((7-4√3+√(45-12√3))/(20-2√3), (-13-2√3+√(45-12√3))/(4(√3-10)))=((58-33√3+√(3(1305-112√3))/194,(136+33√3-√(3(1305-112√3))/388)

甲の1辺=(1-a)=(136+33√3-√(3(1305-112√3)))/194=0.6980…

乙=丙の半径=PQ=√ ((1+a)/2-p)^2+ ((√3/2)(1-a)-√3(1-p)/3))^2)

=√((3a^2-6a*p+4p^2-2p+1)/3)

=√(2(11075-590√3-3√(7856493-1067332√3))/194=0.378…

ちなみに計算はすべてPCにお願いしました...Orz

NO3 「二度漬け白菜」 10/26 13時04分　 受信 更新 11/10

[問題1] 求める4桁の整数は，2025, 3025, 9801 (答)

上2桁の数をx，下2桁の数をyとおく．

問題文の条件より，

(x+y)^2=100*x+y ---(☆)

よって，x^2-2*(50-y)*x+y^2-y=0.

このxについての二次方程式の判別式

(50-y)^2-(y^2-y)=50^2-99*y

が平方数であることが必要．よって，

50^2-99*y=A^2 (Aは0以上の整数) とおける．

(50-A)*(50+A)=9*11*y ---(★)

と変形できる．

y≠0である．(y=0だとすると☆より，x=0 or x=100となるがこれらは不適)

よって y>0 であるから，0≦A≦49 である．

(★)より，(50-A)と(50+A)は，少なくともどちらか一方は

11の倍数だということがわかる．

(50-A)が11の倍数となるのは，A=39,28,17,6の4つの場合がある．

しかし，これらのAの値を(★)に代入すると，いずれの場合も

yが非整数になる．

(50+A)が11の倍数となるのは，A=5,16,27,38,49の5つの場合がある．

このうち，(★)に代入したときにyが整数になるのは A=5 および A=49 の場合のみ．

A=5の場合：(★)より y=25. (☆)に代入して，x=20 or x=30. これらはいずれも適．

A=49の場合：(★)より y=1. (☆)に代入して，x=0 or x=98. 後者のみが適．

以上より，問題文の条件を満たすような4桁の整数は，

2025,3025,9801 である．

[問題2] n=17,18,19,20,21,22,23,24． (答)

√(n^2+1) = m + (2/100) + α

(mは正整数，αは 0≦α＜(1/100)なる実数)

とおける．

α=√(n^2+1)-m-(2/100) および 0≦α＜(1/100) とから，

0≦ √(n^2+1)-m-(2/100)＜(1/100)．よって，

m+(2/100)≦ √(n^2+1)＜m+(3/100). よって，

(m+(2/100))^2≦(n^2+1)＜(m+(3/100))^2 ---(☆)

この不等式から m=n であることがわかる．

(なぜなら，m≦n-1だと仮定すると，(m+1)^2+1≦n^2+1 となる．これと(☆)とから，

(m+1)^2+1＜(m+(3/100))^2. よって，(2-6/100)*m＜(3/100)^2-2＜0となって矛盾．

また，m≧n+1だと仮定すると，n≦m-1 より，n^2+1≦(m-1)^2+1. これと(☆)とから，

(m+(2/100))^2≦(m-1)^2+1. よって，(2+4/100)*m≦(2-4/10000) となって矛盾．)

m=nと(☆)とから，

(n+(2/100))^2≦(n^2+1) かつ (n^2+1)＜(n+(3/100))^2.

これらの2式より，17≦n≦24.

[問題3] 求める和は，26911 (答)

x=yの場合とx>yの場合に分けて考える．

・x=yの場合：

この場合，1/x+1/y=1/100 つまり，1/x+1/x=1/100 となるようなxは， x=200．

よって1/x+1/y=1/100を満たす自然数(x,y)のうちの，x+yの総和は200+200=400.

・x>yの場合：

1/x+1/y=1/100 を変形して，

(x-100)*(y-100)=100^2=(2^4)*(5^4) ---(★)

x,yはともに自然数であるから，(x-100)>0 かつ (y-100)>0 となる．

(x-100)が100より大なる100^2の約数のとき，(y-100)=100^2/(x-100)は100より小なる100^2の約数．

また，(y-100)が100より小なる100^2の約数のとき，(x-100)=100^2/(y-100)は100より大なる100^2の約数．

つまり，(★)を満たす(x-100)と(y-100)は一対一に対応する．

よって，(★)を満たす自然数(x-100,y-100)のうちの，(x-100)+(y-100)の総和

をSとすると，

S=(2^0+2^1+2^2+2^3+2^4)*(5^0+5^1+5^2+5^3+5^4)-100=24111.

よってx>yの場合，(★)を満たす自然数(x,y)のうちの，x+yの総和は，S+100*((4+1)*(4+1)-1)=26511.

以上より求める和は，400+26511=26911.

[追加問題1]

(甲の一辺の長さ)=-((3915/37636)-(84/9409)*3^(1/2))^(1/2)+(33/194)*3^(1/2)+(68/97),

(乙の一辺の長さ)=(-(70708437/354117124-(2401497/88529281)*3^(1/2))^(1/2)-(295/9409)*3^(1/2)+11075/18818)^(1/2) (答)

甲の一辺の長さを r，

乙の一辺の長さを s

とおく．

複素平面上で考える．

図のように，主要な5頂点を表す複素数を

z_1，z_2，z_3，z_4，z_5 とする．

( 図→ https://fpseries.exblog.jp/33261004 )

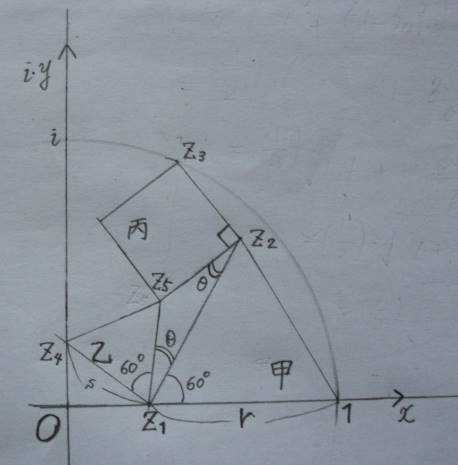
z_1=(1-r)+i*0,

z_2=(1-r/2)+i*(r/2)*(√3)

である．

また，図のようにθをとると，cos(θ)=(r/2)/s=r/(2*s).

これらを使って，z_5,z_4は次のように計算できる．

z_5

=(s/2)*(1+i*√3)*(cos(θ)+i*sin(θ))+z_1

=(1-3*r/4-(s/2)*(√3)*sin(θ))+i*((r/4)*(√3)+(s/2)*sin(θ)).

z_4

=(z_5-z_1)*(cos(π/3)+i*sin(π/3))+z_1

=(1-5*r/4-(s/2)*(√3)*sin(θ))+i*((r/4)*(√3)-(s/2)*sin(θ)).

Re(z_4)=0より，

(s/2)*sin(θ)=(1-5*r/4)/(√3).

これを先のz_5の式に代入して，

z_5=(r/2)+i*(1/6)*(2-r)*√3.

z_3

=(z_5-z_2)*(cos(-π/2)+i*sin(-π/2))+z_2

=(-r)*((2/3)*3^(1/2)+(1/2))+(1/3)*3^(1/2)+1+i*(r*((1/2)*3^(1/2)-1)+1) .

|z_3|=1より，

((-r)*((2/3)*3^(1/2)+(1/2))+(1/3)*3^(1/2)+1)^2+(r*((1/2)*3^(1/2)-1)+1)^2=1.

これを解いて，

r=-((3915/37636)-(84/9409)*3^(1/2))^(1/2)+(33/194)*3^(1/2)+(68/97).

(r=0.6980683…)

また，(sin(θ))^2=1-(cos(θ))^2より，

(2*(1-5*r/4)/(s*√3))^2=1-(r/(2*s))^2.

よって，

s=((r^2)/4+(4/3)*(1-5*r/4)^2)^(1/2)

=(-(70708437/354117124-(2401497/88529281)*3^(1/2))^(1/2)-(295/9409)*3^(1/2)+11075/18818)^(1/2).

(=0.378775412…)

[追加問題2]

甲の一辺の長さは，(1/6)*3^(1/2)，

乙の一辺の長さは，1-(1/6)*3^(1/2),

丙の一辺の長さは，(1/2)*(5-2*3^(1/2))^(1/2)，

丁の一辺の長さは，(2/3)*3^(1/2)-1　(答)

甲の一辺の長さを a とおく．

複素平面上で考える．

図のように，3つの頂点を表す複素数を z_1，z_2，z_3 とする．

( 図→ https://fpseries.exblog.jp/33271664 )

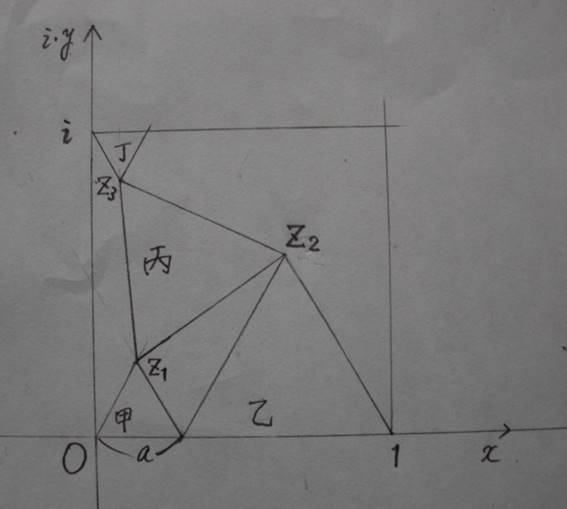
z_1=(1/2)*(a+i*a*√3),

z_2=(1/2)*((1+a)+i*(1-a)*√3)，

z_3

=(z_2-z_1)*(cos(π/3)+i*sin(π/3))+z_1

=((4*a-1)/2)+i*((1/2)*√3).

Re(z_3):(1-Im(z_3))=1:√3 であるから，

((4*a-1)/2):(1-(1/2)*√3)=1:√3.

これを解いて，a=(1/6)*√3.

(丙の一辺の長さ)=|z_2-z_1|=|(1/2)*(1+i*(1-2*a)*√3)|=(1/2)*(5-2*3^(1/2))^(1/2).

(丁の一辺の長さ)=2*Re(z_3)=(2/3)*3^(1/2)-1.

(以上)

NO4「kasama」 10/28 01時27分　　 受信 更新 11/10

寄せられた解答です

＜コメント：今回の問題ですが、追加問題１で悩みました。腕力でねじ伏せるやり方は、あまり好ましいとは思いませんので、二次方程式の解として求まるようにアプローチしました。ところが、導いた乙の長さがあまりにも汚い値（三重根号が外れない）でした。合っているのやら、間違っているのやら？？？しかし、次の２つの方法で検証した結果、大丈夫そうだったので、解答をお送りします。

　・座標系を導入して、出した答えと一致しました。

　・AutoCADで作図すると、それなりの図形になりました。

ただし、答えは美しい形に変形できるかもしれません。＞

＜水の流れ：お疲れ様でした。追加問題１の答えは同じものです＞

NO5「よふかしのつらいおじさん」 11/2 12時09分 受信 更新 11/10

寄せられた解答です

NO6「三角定規」 11/8　 21時25分 受信 更新 11/10

今回ですが, <追加>の問題１がやや自信がありません。

図の作成を手伝ってくれた grapes の数値出力と一致するので, 合っている…？

それにしても, 甲の一辺の厳密解が (Wolfram 出力が) あまりに複雑なので, 数値解のみとしました。

寄せられた解答です

<水の流れ：追加問題１の図で、出題したと甲と乙が入れ替わっていますから、ご注意ください。＞

<水の流れ> 更新 11/10

皆さん、問題や質問に答えてください。一部でも構いませんから, 解答とペンネームを添えて, メールで送ってください。待っています。