�ߘa�U�N�P�Q���W��
 [���ꐯ]
[���ꐯ]
�@�@��448�����w�I�ȘA�������
�@�@�@����W���ԁF11��10���`12��8����
�m�������̉���n
���P�@2021�N����w�i���n�j�������̉���@

�@�@
���Q�@2024�N���É��s����w�i��w���j�������̉���@

���R�@2004�N������w���T�E���T�������̉���
�@�������ʂ̕������������Q��̂R�_�o�C�p�C�q�����̏��������Ă���B
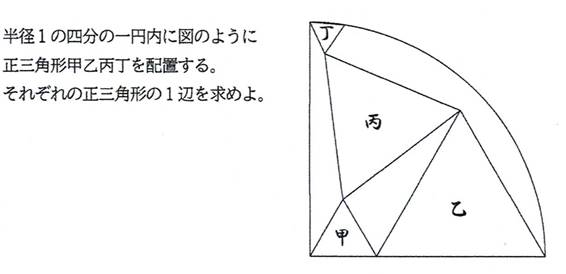
�u�O�p�`�o�p�q��1�ӂ̒���a�̐��O�p�`�ł���A�_�o�C�p��ʂ钼���̌X���͂P�ł���B�v�@���̂Ƃ�,a�̒l�����߂�B
�lj�����i�o��҂́u�W���[�J�[�v�j�@�V��V���[�Y�R,�S���
���1
���Q
�@
NO1�u�W���[�J�[�v �@ 11/10 �@16��01�� ��M �X�V 12/8
��ꂽ����
NO2�u�X���[�N�}���v 11/11 00��44���@ ��M �X�V 12/8
���1 2021�N����w�i���n�j�������̉���
f(��)
=sin^2(��)+1+1/(4sin^2��)+cos^2(��)+1/2+1/(16cos^2(��))
=5/2+(1/(2sin(��))^2+1/(4cos(��))^2)
sin^2(��)=t, cos^2(��)=1-t
(1/(2sin(��))^2+1/(4cos(��))^2)
=1/(4t)+1/(16(1-t))
=(1/16)(4/t+1/(1-t))
f(t)=4/t+1/(1-t)
f�f(t)
=-4/t^2+1/(1-t)^2
=(-4(1-t)^2+t^2)/(t^2*(1-t)^2)
=(-3t^2+8t-4)/(t^2*(1-t)^2)
=-(3t-2)(t-2)/(t^2*(1-t)^2)
=0
0<t<1
t 0 2/3 1 2
f(t) + 0 +
so�ct=2/3 �̂Ƃ��ŏ��l=4/(2/3)+1/(1/3)=9
So�c
Min{f(��)}=5/2+9/16=49/16, sin(��)=��6/3 �̂Ƃ��B
���2 2024�N���É��s����w�i��w���j�������̉���
(1)
3^n-2^n
3,9,7,1�̎���
2,4,8,6�̎���
So�c4������
1,5,-1,-5
�܂�A
n=4k+1�̂Ƃ�1
n=4k+2 �̂Ƃ� 5
n=4k+3 �̂Ƃ� 9
n=4k �̂Ƃ� 5
(2)
3^n-2^n+4n
4n�c4,8,2,6,0 ��5����
1,5,-1,-5��4�����Ƃňȉ���20����
4 8 2 6 0 4 8 2 6 0 4 8 2 6 0 4 8 2 6 0
1 5 9 5 1 5 9 5 1 5 9 5 1 5 9 5 1 5 9 5
5 3 1 1 1 9 7 7 7 5 3 3 3 1 9 9 9 7 5 5
r(s)=7 ��
20�̂���7,8,9,18�Ԗڂ�4��
So�c
n=20(m-1)+7,8,9,18
so�c
a(2024)�́A
2024/4=506
2024��4�̔{��������
So�c
n=18�{20*�i506-1�j=10118�@
���R�@2004�N������w���T�E���T�������̉���
�@�������ʂ̕������������Q��̂R�_�o�C�p�C�q�����̏��������Ă���B
�u�O�p�`�o�p�q��1�ӂ̒���a�̐��O�p�`�ł���A�_�o�C�p��ʂ钼���̌X���͂P�ł���B�v�@���̂Ƃ�,a�̒l�����߂�B
P(p,p^2)
Q(q,q^2)
R(x,x^2)
p<q
(q^2-p^2)/(q-p)=q+p=1
p<q, p+q=1, (p-q)^2+(p^2-q^2)^2=a^2, x^2-(p^2+q^2)/2=-(x-(p+q)/2), (x-p)^2+(x^2-p^2)^2=a^2
(p-q)^2+(p-q)^2=a^2
2(p-q)^2=a^2
p+q=1
���A
p^2+q^2=(a^2+2)/4
(x-p)^2+(x^2-p^2)^2-((x-q)^2+(x^2-q^2)^2)=0
���A
p^4-q^4+p^2-q^2-2x^2(p^2-q^2)-2x(p-q)=0
(p^2+q^2)+1-2x^2-2x=0
2x^2+2x=(a^2+2)/4+1
((x+p+q)/3-x)^2+(((x^2+p^2+q^2)/3-x^2)^2=a^2/3
((1-2x)/3)^2+(((a^2+2)/4-2x^2)/3)^2=a^2/3
So�c
((1-2x)/3)^2+(((a^2+4)/8-(a^2+4)/8+1-2x)/3)^2=a^2/3
���
(1-2x)^2=3a^2/2
2(1-2x)^2=3a^2
8x^2-8x=3a^2-2
8x^2+8x=(a^2+2)+4=a^2+6
3a^2=8x^2-8x+2=(8x^2+8x-6)*3
���A
x=1/2, -5/2
a^2=8x^2+8x-6=0, 24
so�c
a=2��6
���̂Ƃ��A
2(p-q)^2=(2��6)^2 , p+q=1
���
P=((1-2��3)/2,(13-4��3)/4)
Q=((1+2��3)/2,(13+4��3)/4)
((1+2��3)/2-(1-2��3)/2)^2+(((1+2��3)/2)^2-((1-2��3)/2)^2)^2
=24=(2��6)^2
R=(-5/2,25/4)
25/4-13/4=3
-(-5/2-(1/2))=3
(-5/2-(1-2��3)/2)^2+(25/4-(13-4��3)/4)^2=24
�Ŗ������Ă� ^^
�lj����P

�����̗���F����1�ӂ̒l�͒��̂P�ӂł���
NO3�u��x�Ђ����v �@ 11/24 �@10��46�� ��M �X�V 12/8
[���1]
f(��)�̍ŏ��l�� 49/16 (��)
f(��)=(sin(��)+1/(2*sin(��)))^2+(cos(��)+1/(4*cos(��)))^2
=5/2+(1/16)*(4-3*(sin(��))^2)/((sin(��))^2*(1-(sin(��))^2)).
�����ŁCt=4-3*(sin(��))^2 �Ƃ����D
0<(sin(��))^2<1 �ł��邱�Ƃ��C1<t<4.
f(��)��t�̎��ŕ\���ƁC
f(��)=5/2+(9/16)*(1/(-(t-1)*(t-4)/t)).
-(t-1)*(t-4)/t>0�ł��邱�Ƃ��l����ƁC
f(��)���ŏ�
�� -(t-1)*(t-4)/t ���ő�
�� 5-(t+4/t) ���ő�
�� (t+4/t) ���ŏ�
�� t=2
�ł���D
t=2�́Csin(��)=(2/3)^(1/2)�̂Ƃ���������D
[���2]
(1) 3^n-2^n��10�Ŋ������]��́C
n��1(mod 4)�̂Ƃ��C1
n��2(mod 4)�̂Ƃ��C5
n��3(mod 4)�̂Ƃ��C9
n��0(mod 4)�̂Ƃ��C5 �@(��)
(2) a[2024]=10118. (��)
3^1��3,3^2��9,3^3��7,3^4��1,3^5��3,�c
2^1��2,2^2��4,2^3��8,2^4��6,2^5��2,�c
�ł��邩��C
3^1-2^1��1,
3^2-2^2��5,
3^3-2^3��-1��9,
3^4-2^4��-5��5,
3^5-2^5��1,
(�ȉ�����4�ŌJ��Ԃ�)
4*1��4,4*2��8,4*3��2,4*4��6,4*5��0,
4*6��4,4*7��8,4*8��2,4*9��6,4*10��0,
(�ȉ�����5�ŌJ��Ԃ�)
n=1,2,3,�c�ɑ���r[n]�̒l�����ɕ��ׂ�ƁC
���̂悤�Ɏ���20�ŌJ��Ԃ����Ƃ��킩��D
r[n]=
5,3,1,1,1,9,7,7,7,5,3,3,3,1,9,9,9,7,5,5,
5,3,1,1,1,9,7,7,7,5,�c
1�����̒��ɁCr[n]=7�ƂȂ�悤��n��4����D�@�@
r[n]=7�ƂȂ�悤��n�����������ɁC4���̃u���b�N�ɕ��ׂ�ƁC
7,8,9,18 | 27,28,29,38 | 47,48,49,58 |
67,68,69,78 | �c
k�ڂ̃u���b�N�ɕ���4�̐��́C
20*(k-1)+7, 20*(k-1)+8, 20*(k-1)+9,
20*(k-1)+18
�ł���D
����āCa[m]��m�̎��ŕ\���ƁC
a[m]
=20*floor((m-1)/4)
+7*(1+floor((m-1)/4)+floor(-(m-1)/4))
+8*(1+floor((m-2)/4)+floor(-(m-2)/4))
+9*(1+floor((m-3)/4)+floor(-(m-3)/4))
+18*(1+floor((m-4)/4)+floor(-(m-4)/4)).
���̎����g����a[2024]�̒l���v�Z����ƁC
a[2024]=10118.
[���3]
a=2*6^(1/2) (��)
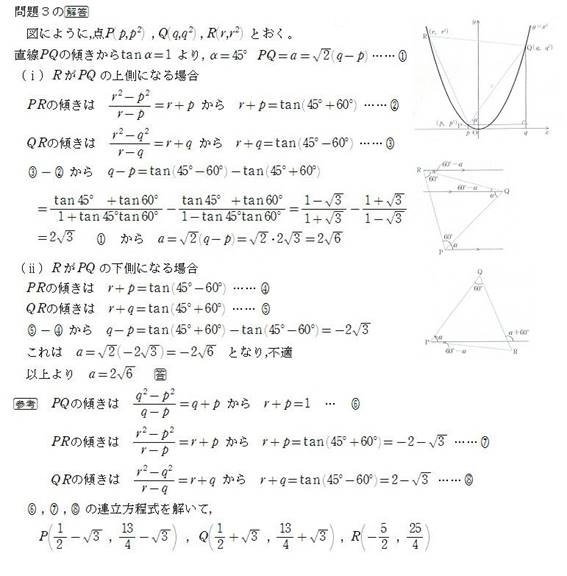
xy���ʂf���ʂƓ��ꎋ���čl����D
�_P,Q,R��\�����f���� z_P,z_Q,z_R �Ƃ���D
z_P=p+i*p^2,
z_Q=q+i*q^2
�Ƃ�����D������ p��q �ł���D
(�_P�Ɠ_Q�͈قȂ�_�ł���Dp=q���Ƃ���ƁCP��Q�͈�v���邱�ƂɂȂ�)
����PQ�̌X����1�ł��邩��C
(p^2-q^2)/(p-q)=1.�@����āCp+q=1.
z_R=(z_Q-z_P)*(cos(��/3)+i*sin(��/3))+z_P
=(1/2)*(q-p)(1+i*(q+p))*(1+i*3^(1/2))+(p+i*p^2)
=(1/2)*(1-2*p)*(1+i)*(1+i*3^(1/2))+(p+i*p^2)
=(1/2)*(1-2*p)*(1-3^(1/2))+p+i*((1/2)*(1-2*p)*(1+3^(1/2))+p^2).
R��y=x^2��̓_�ł��邩��C
(1/2)*(1-2*p)*(1+3^(1/2))+p^2=((1/2)*(1-2*p)*(1-3^(1/2))+p)^2.
����āC(1-2*p)*(p+3^(1/2)-1/2)=0.
�����ŁC1-2*p��0�ł���D
(1-2*p=0���Ƃ���ƁCp=1/2�ƂȂ�. p+q=1�Ƃ���Cq=1/2.
�܂�Cp=q�ƂȂ��āC�s����)
����āC
p=1/2-3^(1/2).
a=2^(1/2)*|q-p|=2^(1/2)*|1-2*p|=2*6^(1/2).
[�lj����1]
�b�̈�ӂ̒����́C(1/4)*((12)^(1/4)+1-3^(1/2))�C
���̈�ӂ̒����́C(1/4)*(-(12)^(1/4)+3+3^(1/2)),
���̈�ӂ̒����́C((3/4)*3^(1/2)+1-(3/8)*((108)^(1/4)+(12)^(1/4)))^(1/2)�C
���̈�ӂ̒����́C((1/4)*(9-3*3^(1/2)))^(1/2)-((1/4)*(1+3^(1/2)))^(1/2).
��447��[�lj����2]�̉Ŏg�p�����}�����̂܂g���D
�b�̈�ӂ̒����� a �Ƃ����D
���O�p�`����z_3�ȊO��2�̒��_�̂����C������ɂȂ��_�� z_4�Ƃ���D
z_1=(1/2)*(a+i*a*3^(1/2)),
z_2=(1/2)*((1+a)+i*(1-a)*3^(1/2))�C
z_3=(z_2-z_1)*(cos(��/3)+i*sin(��/3))+z_1
=((4*a-1)/2)+i*((1/2)*3^(1/2)).
z_4=(i-z_3)*(cos(-��/3)+i*sin(-��/3))+z_3
=(1/2)*(2*a+3^(1/2)-2)+i*(a*3^(1/2)+1/2).
|z_4|=1���C
((1/2)*(2*a+3^(1/2)-2))^2+((a*3^(1/2)+1/2))^2=1.
����������āC
a=(1/4)*((12)^(1/4)+1-3^(1/2)).
(=0.2822897�c)
(���̈�ӂ̒���)=|z_2-z_1|=((3/4)*3^(1/2)+1-(3/8)*((108)^(1/4)+(12)^(1/4)))^(1/2),
(���̈�ӂ̒���)=|i-z_3|=((1/4)*(9-3*3^(1/2)))^(1/2)-((1/4)*(1+3^(1/2)))^(1/2).
[�lj����2]
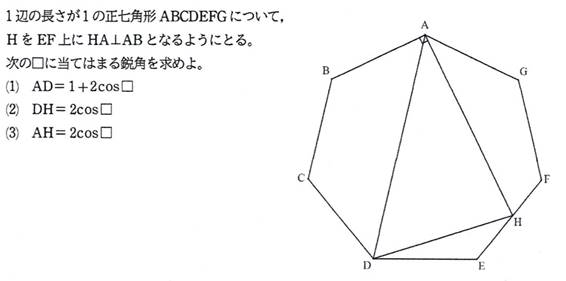
(1) AD=1+2*cos((360/7)��)�C
(2) DH=2*cos(45��)�C
(3) AH=2*cos((90/7)��) �@(��)
��=(1/7)*90���Ƃ����D
�C�ӂ̐��� k �ɑ��āC����
sin(k*��)=cos(90��- k*��)=cos(7*��-k*��)=cos((7-k)*��)
�����藧�D
�ȉ��C���̓�����f��Ȃ��Ɏg���D
�E�܂��CAD�����߂�F
����DE�̒��_��M�Ƃ���D
��DOE=(1/7)*360��= 4*�� �ł��邱�Ƃ��C
��DAM=(1/2)*(��DAE)=(1/2)*(1/2)*(��DOE)=��.
������CAD�͎��̂悤�Ɍv�Z�ł���D
AD
=DM/sin(��DAM)
=(1/2)/sin(��)
=1/(2*sin(��)) ---(��)
=cos(��)/(2*sin(��)*cos(��))
=sin(6*��)/sin(2*��)
=(sin(6*��)-sin(2*��)+sin(2*��))/sin(2*��)
=(2*sin(2*��)*cos(4*��)+sin(2*��))/sin(2*��)
=2*cos(4*��)+1.
�E���ɁCAH�����߂�F
��MAH=��BAH-��BAM =90��- 5*��=2*��.
��EAH=��MAH-��MAE =2*��-��=��.
��AEH=��AEG+��GEF =2*��+2*��=4*��.
��AHE=180��-(��EAH+��AEH)=14*��-(��+4*��)=9*��.
��AEH�ɐ����藝��p���āC
AH/sin(4*��)=AE/sin(9*��).
����āC
AH=AE*(sin(4*��)/sin(9*��))
=AE*(cos(3*��)/cos(-2*��))
=AD*(cos(3*��)/cos(2*��))
=cos(3*��)/(2*sin(��)*cos(2*��)) (��(��)���CAD=1/(2*sin(��)))
=cos(3*��)*cos(��)/(2*sin(��)*cos(��)*cos(2*��))
=cos(3*��)*cos(��)/(sin(2*��)*cos(2*��))
=cos(3*��)*cos(��)/((1/2)*sin(4*��))
=cos(3*��)*cos(��)/((1/2)*cos(3*��))
=2*cos(��).
�E���ɁCDH�����߂�F
��DAH=��DAM+��MAH=��+2*��=3*��.
��ADH�ɐ����藝��p���āC
DH^2
=AD^2+AH^2-2*AD*AH*cos(��DAH)
=(1/(2*sin(��)))^2+(2*cos(��))^2-2*(1/(2*sin(��)))*(2*cos(��))*cos(3*��)
=(1/(2*sin(��)))^2*(1+4*(2*sin(��)*cos(��))^2-4*2*sin(��)*cos(��)*cos(3*��))
=(1/(2*sin(��)))^2*(1+4*(sin(2*��))^2-4*sin(2*��)*cos(3*��))
=(1/(2*sin(��)))^2*(1+4*(cos(5*��))^2-4*cos(5*��)*cos(3*��))
=(1/(2*sin(��)))^2*(1+4*cos(5*��)*(cos(5*��)-cos(3*��)))
=(1/(2*sin(��)))^2*(1-8*cos(5*��)*sin(4*��)*sin(��))
=(1/(2*sin(��)))^2*(1-8*cos(5*��)*cos(3*��)*cos(6*��))
=(1/(2*sin(��)))^2*(1-4*(cos(8*��)+cos(2*��))*cos(6*��))
=(1/(2*sin(��)))^2*(1-4*(-cos(6*��)+cos(2*��))*cos(6*��))
=(1/(2*sin(��)))^2*(1+4*(cos(6*��))^2-4*cos(2*��)*cos(6*��))
=(1/(2*sin(��)))^2*(1+4*(sin(��))^2-4*cos(2*��)*cos(6*��))
=1+(1/(2*sin(��)))^2*(1-4*cos(2*��)*cos(6*��))
=1+(1/(2*sin(��)))^2*(1-4*cos(2*��)*sin(��))
=1+(1/(4*sin(��)*cos(��)*sin(��)))*cos(��)*(1-4*cos(2*��)*sin(��))
=1+(1/(4*sin(��)*cos(��)*sin(��)))*(cos(��)-4*cos(2*��)*sin(��)*cos(��))
=1+(1/(2*sin(2*��)*sin(��)))*(cos(��)-sin(4*��))
=1+(1/(2*sin(2*��)*sin(��)))*(cos(��)-cos(3*��))
=1+(1/(2*sin(2*��)*sin(��)))*2*(sin(2*��)*sin(��))
=1+1
=2.
����āCDH=2^(1/2).
(�ȏ�)
�����̗���F�����Ɏ���v�Z�ߒ��ɋ�J�̐Ղ��f���܂��B��ςȋC�͂��K�v�ł��B���ӂ��܂��B��
NO4�ukasama�v �@ 11/25 �@00��59�� ��M �X�V 12/8
��ꂽ����
�����̗���F�@�⑫�P�E�Q�� �v�Z�ߒ��A�⑫�R��
���{�p�̌����L�q���Ă���A�Q�l�ɂȂ�܂��B��
NO5�u��ӂ����̂炢��������v 11/29 17��02�� ��M �X�V
12/8
��ꂽ����
�����̗���F�lj����P�̕��̒l���W���J�[����ƌ��ʂ����l���Ă��Ȃ������̂ŁA�u��ӂ����̂炢��������v�ɐq�˂Ă݂܂����B
�u��ӂ����̂炢��������v 11/30 17��35�� ��M �X�V
12/8
�@�����̗���F�Ԏ��ł��B�r���܂Ō��Z�����̂ł����A�Ō�܂ŏo���Ȃ��Đ\����܂���B��

NO6�u�O�p��K�v 12/4�@ 15��23�� ��M �X�V 12/8
�����������
����ł����C�s�lj��t��[���Q]�ɋ�J���܂����B
�u���ł��邾�낤�v�Ȃǂƍ����������Ă����̂ł����c�I
(1)�͂����o���܂������C(2)(3)�œڍ��I
���̌`��(2)(3)�Ƃ��� 2cos�� �Ȃ̂ŁC���̌`�ɂ����Ă������Ƌ�킵�����ʂ����|�[�g�ł����B
AH �̕��͐}�`�I�ɉ��Ƃ��Ȃ�܂�����, DH��2cos(��/4) �̐}�`�I�ȈӖ��͖����ɁH�ł��B
�F�l�̑N�₩�ȉɊ��҂��܂��B
�u���̗���v �@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�X�V 12/8


�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���, �ƃy���l�[����Y����, ���[���ő����Ă��������B�҂��Ă��܂��B
