�ߘa�V�N�R���R�O��
 [���ꐯ]
[���ꐯ]
�@�@��452�����w�I�ȘA�������
�@�@�@����W���ԁF�R���Q���`�R���R�O����
�m�P�ʕ����n
�@���q���P�̕�����P�ʕ����Ƃ����A�������قȂ�P�ʕ����̘a�ŕ\�����Ƃ��P�ʕ��������Ƃ����B
���́A�P�ʕ��������̕��@�͖����ʂ肠��A�ؖ����邱�Ƃ��\�ł��B
��q�ɂ���Q�l���Q�Ƃ��������B
�P�ʕ��������̕��@�́A2�ʂ肠��܂��B
�P�@������������������A�ő�̒P�ʕ������Ђ��Ă������@
�Q�@�s�����ɂ���āA����ɂ��Ă͂܂鎩�R�������ڂ��Ă������@
�P�ʕ��������̕��@�P
�@�@���Ƃ̕�������A�����菬�����ő�̒P�ʕ������Ђ��B
�A�@���̌��ʂ��P�ʕ����Ȃ�I���B�P�ʕ����łȂ��Ȃ�A���̕�����菬�����ő�̒P�ʕ������Ђ��B
�B�@�A���J��Ԃ��B
���@�L����̌v�Z�ŕK���P�ʕ������o�ꂷ��B
��@ ![]() �̒P�ʕ�������
�̒P�ʕ�������
�@�@![]()
![]() �@��菬�����ő�̒P�ʕ����́A
�@��菬�����ő�̒P�ʕ����́A ![]() �@�Ȃ̂ŁA
�@�Ȃ̂ŁA
![]() ���@
���@![]()
�A�@ ![]() �͒P�ʕ����̂��߁A�����I���B
�͒P�ʕ����̂��߁A�����I���B
�P�ʕ��������̕��@�Q
�@�@���Ƃ̕��� ![]() (x<y) �Ƃ����B
(x<y) �Ƃ����B
�A�@x �ɂ��Ă͂܂�\���̂��鎩�R�������߂�B
�B�@ x �����ꂼ�������A���̂Ƃ���y �̒l�����R���i![]() ���P�ʕ���)�Ȃ�I�����A�����łȂ�����̕����ɂ���(1)���瓯����Ƃ��s���Ă����B
���P�ʕ���)�Ȃ�I�����A�����łȂ�����̕����ɂ���(1)���瓯����Ƃ��s���Ă����B
�� x �ɂ��Ă͂܂�\���̂��鎩�R���́An ���傫���A2n ��菬���������ƂȂ�܂��B
�����ŁA���ł�
���@![]() �̂悤�ɂR�̒P�ʕ����ɕ����ł��܂��B
�̂悤�ɂR�̒P�ʕ����ɕ����ł��܂��B
�P���S���P�ʕ����ɕ������Ă��������B
�]�͖��@�P���T�̈قȂ��P�ʕ����ɕ�������ƁB���g�ɂȂ�܂����B
���̏�ŁA����������ɂ́A�����Ȏ��Ԃ�������A�r���Œ��߂܂����B�@
�N���APC�ŋ��߂Ē����܂��B
�@�@�@�@�@�@
�Q�l�����@BLUEBACKS�@��w�Ō�鐔�_�̐��E�@��������@�u�k��
�Q�l��


�lj�����i�o��҂́u�W���[�J�[�v�j�@�V��V���[�Y11,12���
�@����ŏI���ł��B
���1
���Q
�@
NO1�u�O�p��K�v 03/02 21��42���@ ��M �X�V 3/30
[���452] (�]�͖��) 1��1/a+1/b+1/c+1/d+1/e
(a<b<c<d<e)�ɂ��܂���
�Q�l�������L�`���Ɠǂ�ł��炸, (���1 �� �]�͖���) �܂��L�`���Ƃ͍l���Ă��Ȃ��̂ł����C
> �N���A PC �ŋ��߂Ē����܂��B
�Ƃ������̂ŁC�G�N�Z���Ń}�N����g�݁C���̗�̂��߂Ă݂܂����B
�Y�t �G�N�Z���t�@�C���u1��5�̒P�ʕ����̘a��.xlsm�v�������������B
e��100 �� 42�́Ce��200 �� 57�� ���̗Ⴊ����悤�ł��B
�u�O�p��K�v 03/15 09��37���@ ��M �X�V 3/30
�u�O�p��K�v 03/16 09��18���@ ��M �X�V 3/30
�O��C�����ꂽ������
NO2�u�W���[�J�[�v �@ 03/04 �@�@ 16��13�� ��M �X�V 3/30
�u�W���[�J�[�v �@ 03/07�@�@ �@21��31�� ��M �X�V 3/30
�O��\�͖��̉�@���lj�������������
NO3�u���j���w�ҁv �@ 03/05 12��32���@ ��M �X�V 3/30
[��]
(1/x)+(1/y)+(1/z)+(1/w)=1 --------- (1)
����4�̎��R��x,y,z,w (0<x<y<z<w)�����߂�B
(1)�����0<x<y<z<w���A
(1/x)<(1/x)+(1/y)+(1/z)+(1/w)=1
����āA
x>1 -------- (2)
�ł���B
�܂��A���ɁAx>=3�Ȃ�A
(1/x)+(1/y)+(1/z)+(1/w)<=1/3+1/4+1/5+1/6=19/20<1
���A(1)�͐������Ȃ��B
����āAx<3 ------- (3)
���R��x��(2),(3)�����̂ŁAx=2�ł���B
(1)��x=2�������āA
(1/y)+(1/z)+(1/w)=1/2 ---------- (4)
2<y<z<w���A���ɁAy>=6�Ȃ��
(1/y)+(1/z)+(1/w)<=1/6+1/7+1/8=73/168<1/2
�ƂȂ�̂ŁA(4)�͐������Ȃ��B
����āA2<y<6�ł���B
(i)y=3�̂Ƃ�
(4)��y=3�������āA
(1/z)+(1/w)=1/6 -------- (5)
6*(z+w)=z*w
(z-6)*(w-6)=36
(5)���
z>6
(z-6),(w-6)�́A36�̖ŁA0<x-6<w-6�Ȃ̂ŁA
(z-6,w-6)=(1,36),(2,18),(3,12),(4,9)
(z,w)=(7,42),(8,24),(9,18),(10,15)
����āA
(x,y,z,w)=(2,3,7,42),(2,3,8,24),(2,3,9,18),(2,3,10,15)
(ii)y=4�̂Ƃ�
(4)��y=4�������āA
(1/z)+(1/w)=1/4 -------- (6)
4*(z+w)=z*w
(z-4)*(w-4)=16
(6)���
z>4
(z-4),(w-4)�́A16�̖ŁA0<z-4<w-4�Ȃ̂ŁA
(z-4,w-4)=(1,16),(2,8)
(z,w)=(5,20),(6,12)
����āA
(x,y,z,w)=(2,4,5,20),(2,4,6,12)
(iii)y=5�̂Ƃ�
(4)��y=5�������āA
(1/z)+(1/w)=3/10 -------- (7)
10*(z+w)=3*z*w
(3*z-10)*(3*w-10)=100
5<z<w���A����(3*z-10),(3*w-10)�́A100�̖ŁA0<3*z-10<3*w-10�Ȃ̂ŁA
(3*z-10,3*w-10)=(1,100),(2,50),(4,25),(5,20)
(z,w)=(11/3,110/3),(4,20),(14/3,35/3),(5,10)
���̒��ŁAz,w�����R���ŁAz>5�ƂȂ���̂͑��݂��Ȃ��B
(i),(ii),(iii)���A
(x,y,z,w)=(2,3,7,42),(2,3,8,24),(2,3,9,18),(2,3,10,15),(2,4,5,20),(2,4,6,12)
(1)�̎��R����(x,y,z,w)��0<x<y<z<w�������̂́A6�ł���B
1/2+1/3+1/7+1/42=1
1/2+1/3+1/8+1/24=1
1/2+1/3+1/9+1/18=1
1/2+1/3+1/10+1/15=1
1/2+1/4+1/5+1/20=1
1/2+1/4+1/6+1/12=1
[�Q�l]
1��n�̕���̈قȂ�P�ʕ����̘a�ŕ\�����@�̐���Pari/GP�̃v���O�������쐬���āA
�v�Z�����Ă݂܂����B
���ʂ́A�ȉ��̒ʂ�ł��B
���R��n>=2�ɑ��āA
S(n)={[x_1,x_2,x_3,...,x_n] :(1/x_1)+(1/x_2)+(1/x_3)+...+(1/x_n)=1,
x_1,x_2,x_3,...,x_n�͎��R��, 0<x_1<x_2<x_3<...<x_n }
�Ƃ���B
#S(2)=0
#S(3)=1
#S(4)=6
#S(5)=72
#S(6)=2320�@�@�@ (�Y�t�t�@�C���Q��)
#S(7)=249264 (�Y�t�t�@�C���Q��)
#S(8)=??? (157���ȏ�)
[Pari/GP�ɂ��v�Z����]
GP/PARI CALCULATOR Version 2.15.0 (released)
amd64 running netbsd (x86-64/GMP-6.1.2 kernel) 64-bit version
compiled: Oct 15 2022, gcc version 5.5.0 (nb2 20180327)
threading engine: single
(readline v7.0 enabled, extended help enabled)
Copyright (C) 2000-2022 The PARI Group
PARI/GP is free software, covered by the GNU General Public License, and comes WITHOUT ANY WARRANTY WHATSOEVER.
Type ? for help, \q to quit.
Type ?18 for how to get moral (and possibly technical) support.
parisize = 6144000000, primelimit = 100000000
(08:03) gp > sss2a(1)
%1 = 0
(08:03) gp > sss3a(1)
1:[2, 3, 6]
%2 = 1
(08:04) gp > sss4a(1)
1:[2, 3, 7, 42]
2:[2, 3, 8, 24]
3:[2, 3, 9, 18]
4:[2, 3, 10, 15]
5:[2, 4, 5, 20]
6:[2, 4, 6, 12]
%3 = 6
(08:04) gp > sss5a(1)
1:[2, 3, 7, 43, 1806]
2:[2, 3, 7, 44, 924]
3:[2, 3, 7, 45, 630]
4:[2, 3, 7, 46, 483]
5:[2, 3, 7, 48, 336]
6:[2, 3, 7, 49, 294]
7:[2, 3, 7, 51, 238]
8:[2, 3, 7, 54, 189]
9:[2, 3, 7, 56, 168]
10:[2, 3, 7, 60, 140]
11:[2, 3, 7, 63, 126]
12:[2, 3, 7, 70, 105]
13:[2, 3, 7, 78, 91]
14:[2, 3, 8, 25, 600]
15:[2, 3, 8, 26, 312]
16:[2, 3, 8, 27, 216]
17:[2, 3, 8, 28, 168]
18:[2, 3, 8, 30, 120]
19:[2, 3, 8, 32, 96]
20:[2, 3, 8, 33, 88]
21:[2, 3, 8, 36, 72]
22:[2, 3, 8, 40, 60]
23:[2, 3, 8, 42, 56]
24:[2, 3, 9, 19, 342]
25:[2, 3, 9, 20, 180]
26:[2, 3, 9, 21, 126]
27:[2, 3, 9, 22, 99]
28:[2, 3, 9, 24, 72]
29:[2, 3, 9, 27, 54]
30:[2, 3, 9, 30, 45]
31:[2, 3, 10, 16, 240]
32:[2, 3, 10, 18, 90]
33:[2, 3, 10, 20, 60]
34:[2, 3, 10, 24, 40]
35:[2, 3, 11, 14, 231]
36:[2, 3, 11, 15, 110]
37:[2, 3, 11, 22, 33]
38:[2, 3, 12, 13, 156]
39:[2, 3, 12, 14, 84]
40:[2, 3, 12, 15, 60]
41:[2, 3, 12, 16, 48]
42:[2, 3, 12, 18, 36]
43:[2, 3, 12, 20, 30]
44:[2, 3, 12, 21, 28]
45:[2, 3, 14, 15, 35]
46:[2, 4, 5, 21, 420]
47:[2, 4, 5, 22, 220]
48:[2, 4, 5, 24, 120]
49:[2, 4, 5, 25, 100]
50:[2, 4, 5, 28, 70]
51:[2, 4, 5, 30, 60]
52:[2, 4, 5, 36, 45]
53:[2, 4, 6, 13, 156]
54:[2, 4, 6, 14, 84]
55:[2, 4, 6, 15, 60]
56:[2, 4, 6, 16, 48]
57:[2, 4, 6, 18, 36]
58:[2, 4, 6, 20, 30]
59:[2, 4, 6, 21, 28]
60:[2, 4, 7, 10, 140]
61:[2, 4, 7, 12, 42]
62:[2, 4, 7, 14, 28]
63:[2, 4, 8, 9, 72]
64:[2, 4, 8, 10, 40]
65:[2, 4, 8, 12, 24]
66:[2, 4, 9, 12, 18]
67:[2, 4, 10, 12, 15]
68:[2, 5, 6, 8, 120]
69:[2, 5, 6, 9, 45]
70:[2, 5, 6, 10, 30]
71:[2, 5, 6, 12, 20]
72:[3, 4, 5, 6, 20]
time = 1 ms.
%4 = 72
(08:04) gp > sss6c(1)
time = 23 ms.
%5 = 2320
(08:04) gp > sss7c(1)
time = 8,337 ms.
%6 = 249264
�����̗���F[Pari/GP�̃v���O����(n=4,5�̏ꍇ)]�͊��������Ă��������܂��B��
<���̗���F���͈̉قȂ�P�ʕ����̘a���l���Ă��܂��B>
�u���j���w�ҁv �@ 03/06 14��23���@ ��M �X�V 3/30
[�Q�l2]
�P�ʕ���(����̏d��������)�̘a�ŕ\���ꍇ�ɂ��Ă��A�v�Z���܂����B
1��4�̒P�ʕ���(����̏d��������)�̘a�ŕ\�����@�́A�ȉ���14�ʂ�ł���B
1/2+1/3+1/7+1/42=1
1/2+1/3+1/8+1/24=1
1/2+1/3+1/9+1/18=1
1/2+1/3+1/10+1/15=1
1/2+1/3+1/12+1/12=1
1/2+1/4+1/5+1/20=1
1/2+1/4+1/6+1/12=1
1/2+1/4+1/8+1/8=1
1/2+1/5+1/10+1/10=1
1/2+1/6+1/6+1/6=1
1/3+1/3+1/4+1/12=1
1/3+1/3+1/6+1/6=1
1/3+1/4+1/4+1/6=1
1/4+1/4+1/4+1/4=1
���R��n>=2�ɑ��āA
T(n)={[x_1,x_2,x_3,...,x_n] :(1/x_1)+(1/x_2)+(1/x_3)+...+(1/x_n)=1,
x_1,x_2,x_3,...,x_n�͎��R��, 0<x_1<=x_2<=x_3<=...<=x_n }
�Ƃ���B
#T(2)=1
#T(3)=3
#T(4)=14
#T(5)=147
#T(6)=3483�@�@ (�Y�t�t�@�C���Q��)
#T(7)=294314 (�Y�t�t�@�C���Q��)
#T(8)=???
<���̗���F6�A7�łł���P�ʕ����̘a���P�ƂȂ�ꍇ��4���A6���ƂȂ�Ƃ͋����ł��E�B
[Pari/GP�ɂ��v�Z����]
(09:24) gp > sss2(1)
1:[2, 2]
%2 = 1
(09:24) gp > sss3(1)
1:[2, 3, 6]
2:[2, 4, 4]
3:[3, 3, 3]
%3 = 3
(09:31) gp > sss4(1,1)
1:[2, 3, 7, 42]
2:[2, 3, 8, 24]
3:[2, 3, 9, 18]
4:[2, 3, 10, 15]
5:[2, 3, 12, 12]
6:[2, 4, 5, 20]
7:[2, 4, 6, 12]
8:[2, 4, 8, 8]
9:[2, 5, 5, 10]
10:[2, 6, 6, 6]
11:[3, 3, 4, 12]
12:[3, 3, 6, 6]
13:[3, 4, 4, 6]
14:[4, 4, 4, 4]
%2 = 14
(09:31) gp > sss5(1,1)
1:[2, 3, 7, 43, 1806]
2:[2, 3, 7, 44, 924]
3:[2, 3, 7, 45, 630]
4:[2, 3, 7, 46, 483]
5:[2, 3, 7, 48, 336]
6:[2, 3, 7, 49, 294]
7:[2, 3, 7, 51, 238]
8:[2, 3, 7, 54, 189]
9:[2, 3, 7, 56, 168]
10:[2, 3, 7, 60, 140]
11:[2, 3, 7, 63, 126]
12:[2, 3, 7, 70, 105]
13:[2, 3, 7, 78, 91]
14:[2, 3, 7, 84, 84]
15:[2, 3, 8, 25, 600]
16:[2, 3, 8, 26, 312]
17:[2, 3, 8, 27, 216]
18:[2, 3, 8, 28, 168]
19:[2, 3, 8, 30, 120]
20:[2, 3, 8, 32, 96]
21:[2, 3, 8, 33, 88]
22:[2, 3, 8, 36, 72]
23:[2, 3, 8, 40, 60]
24:[2, 3, 8, 42, 56]
25:[2, 3, 8, 48, 48]
26:[2, 3, 9, 19, 342]
27:[2, 3, 9, 20, 180]
28:[2, 3, 9, 21, 126]
29:[2, 3, 9, 22, 99]
30:[2, 3, 9, 24, 72]
31:[2, 3, 9, 27, 54]
32:[2, 3, 9, 30, 45]
33:[2, 3, 9, 36, 36]
34:[2, 3, 10, 16, 240]
35:[2, 3, 10, 18, 90]
36:[2, 3, 10, 20, 60]
37:[2, 3, 10, 24, 40]
38:[2, 3, 10, 30, 30]
39:[2, 3, 11, 14, 231]
40:[2, 3, 11, 15, 110]
41:[2, 3, 11, 22, 33]
42:[2, 3, 12, 13, 156]
43:[2, 3, 12, 14, 84]
44:[2, 3, 12, 15, 60]
45:[2, 3, 12, 16, 48]
46:[2, 3, 12, 18, 36]
47:[2, 3, 12, 20, 30]
48:[2, 3, 12, 21, 28]
49:[2, 3, 12, 24, 24]
50:[2, 3, 13, 13, 78]
51:[2, 3, 14, 14, 42]
52:[2, 3, 14, 15, 35]
53:[2, 3, 14, 21, 21]
54:[2, 3, 15, 15, 30]
55:[2, 3, 15, 20, 20]
56:[2, 3, 16, 16, 24]
57:[2, 3, 18, 18, 18]
58:[2, 4, 5, 21, 420]
59:[2, 4, 5, 22, 220]
60:[2, 4, 5, 24, 120]
61:[2, 4, 5, 25, 100]
62:[2, 4, 5, 28, 70]
63:[2, 4, 5, 30, 60]
64:[2, 4, 5, 36, 45]
65:[2, 4, 5, 40, 40]
66:[2, 4, 6, 13, 156]
67:[2, 4, 6, 14, 84]
68:[2, 4, 6, 15, 60]
69:[2, 4, 6, 16, 48]
70:[2, 4, 6, 18, 36]
71:[2, 4, 6, 20, 30]
72:[2, 4, 6, 21, 28]
73:[2, 4, 6, 24, 24]
74:[2, 4, 7, 10, 140]
75:[2, 4, 7, 12, 42]
76:[2, 4, 7, 14, 28]
77:[2, 4, 8, 9, 72]
78:[2, 4, 8, 10, 40]
79:[2, 4, 8, 12, 24]
80:[2, 4, 8, 16, 16]
81:[2, 4, 9, 9, 36]
82:[2, 4, 9, 12, 18]
83:[2, 4, 10, 10, 20]
84:[2, 4, 10, 12, 15]
85:[2, 4, 12, 12, 12]
86:[2, 5, 5, 11, 110]
87:[2, 5, 5, 12, 60]
88:[2, 5, 5, 14, 35]
89:[2, 5, 5, 15, 30]
90:[2, 5, 5, 20, 20]
91:[2, 5, 6, 8, 120]
92:[2, 5, 6, 9, 45]
93:[2, 5, 6, 10, 30]
94:[2, 5, 6, 12, 20]
95:[2, 5, 6, 15, 15]
96:[2, 5, 7, 7, 70]
97:[2, 5, 8, 8, 20]
98:[2, 5, 10, 10, 10]
99:[2, 6, 6, 7, 42]
100:[2, 6, 6, 8, 24]
101:[2, 6, 6, 9, 18]
102:[2, 6, 6, 10, 15]
103:[2, 6, 6, 12, 12]
104:[2, 6, 7, 7, 21]
105:[2, 6, 8, 8, 12]
106:[2, 6, 9, 9, 9]
107:[2, 7, 7, 7, 14]
108:[2, 8, 8, 8, 8]
109:[3, 3, 4, 13, 156]
110:[3, 3, 4, 14, 84]
111:[3, 3, 4, 15, 60]
112:[3, 3, 4, 16, 48]
113:[3, 3, 4, 18, 36]
114:[3, 3, 4, 20, 30]
115:[3, 3, 4, 21, 28]
116:[3, 3, 4, 24, 24]
117:[3, 3, 5, 8, 120]
118:[3, 3, 5, 9, 45]
119:[3, 3, 5, 10, 30]
120:[3, 3, 5, 12, 20]
121:[3, 3, 5, 15, 15]
122:[3, 3, 6, 7, 42]
123:[3, 3, 6, 8, 24]
124:[3, 3, 6, 9, 18]
125:[3, 3, 6, 10, 15]
126:[3, 3, 6, 12, 12]
127:[3, 3, 7, 7, 21]
128:[3, 3, 8, 8, 12]
129:[3, 3, 9, 9, 9]
130:[3, 4, 4, 7, 42]
131:[3, 4, 4, 8, 24]
132:[3, 4, 4, 9, 18]
133:[3, 4, 4, 10, 15]
134:[3, 4, 4, 12, 12]
135:[3, 4, 5, 5, 60]
136:[3, 4, 5, 6, 20]
137:[3, 4, 6, 6, 12]
138:[3, 4, 6, 8, 8]
139:[3, 5, 5, 5, 15]
140:[3, 5, 5, 6, 10]
141:[3, 6, 6, 6, 6]
142:[4, 4, 4, 5, 20]
143:[4, 4, 4, 6, 12]
144:[4, 4, 4, 8, 8]
145:[4, 4, 5, 5, 10]
146:[4, 4, 6, 6, 6]
147:[5, 5, 5, 5, 5]
time = 1 ms.
%5 = 147
(09:31) gp > sss5(1,0)
time = 1 ms.
%6 = 147
(09:31) gp > sss6(1,0)
time = 18 ms.
%7 = 3462
(09:32) gp > sss7(1,0)
time = 9,275 ms.
%8 = 294314
�����̗���F[Pari/GP�̃v���O����(n=4,5�̏ꍇ)]�͊��������Ă��������܂��B��
NO4�u�X���[�N�}���v 03/06 20��03���@ ��M �X�V 3/30
��� �P�ʕ���3 or 4�̘a��1
1/a+1/b+1/c+1/d=1
a<b<c<d
4/a>1, 4/d<
So�ca��3�ȉ��Ad��5�ȏ�
(1) a=3
2/3=1/b+1/c+1/d
3/b>2/3�c9/2>b�E�E�Eb��4�ȉ��A
b=4
2/3-1/4=5/12=1/c+1/d
5/12<2/c�c24/5>c�cc��4�ȉ��E�E�Eb=c=4�œK���Ȃ�
(2) a=2
1/2=1/b+1/c+1/d
3/b>1/2�c6>b�E�E�Eb��5, 4, 3
(21) b=5
1/2-1/5=3/10<2/c�cc<20/3�E�E�Ec��6�ȉ�
3/10-1/6=(18-10)/60�E�E�EX
(22) b=4
1/2-1/4=1/4<2/c�E�E�Ec��7�ȉ�
1/4-1/7=(7-4)/28�E�E�EX
1/4-1/6=(6-4)/24=1/12
1/4-1/5=1/20
(23) b=3
1/2-1/3=1/6<2/c�E�E�Ec��12����
1/6-1/11=(11-6)/66�E�E�EX
1/6-1/10=(10-6)/60=1/15
1/6-1/9=(9-6)/54=1/18
1/6-1/8=(8-6)/48=1/24
1/6-1/7=1/42
���ǁc
1/2+1/3+1/10+1/15
1/2+1/3+1/9+1/18
1/2+1/3+1/8+1/24
1/2+1/3+1/7+1/42
1/2+1/4+1/6+1/12
1/2+1/4+1/5+1/20
���l�ɂ���
1/a+1/b+1/c+1/d+1/e=1
5/a>1�E�E�Ea��4�ȉ�
(1) a=4
3/4<4/b�cb<16/3�E�E�Eb��5�ȉ�
3/4-1/5=(15-4)/20=11/20<3/c�cc/60/11�E�E�Ec��5�ȉ���X
(2) a=3
2/3<4/b�cb<6�E�E�Eb��5�ȉ�
(21)b=5
2/3-1/5=(10-3)/15=7/15<3/c�cc<45/7�E�E�Ec��6�ȉ�
7/15-1/6=(42-15)/90=27/90=3/10<2/d�cd<20/3�E�E�Ed��6�ȉ���X
(22)b=4
2/3-1/4=(8-3)/12=5/12<3/c�cc<36/5�E�E�Ec�͂V�ȉ�
(31)c=5
5/12-1/5=(25-12)/60=13/60<2/d�cd<120/13�E�E�Ed�͂X�ȉ�
13/60-1/9=(117-60)/540=57/540�E�E�EX
13/60-1/8=(104-60)/480=44/480�E�E�EX
13/60-1/7=(91-60)/420=31/420�E�E�EX
13/60-1/6=(78-60)/360=18/360=1/20
1/3+1/4+1/5+1/6+1/20
(32)c=6
5/12-1/6=(30-12)/72=18/72=1/4<2/d�cd<8�E�E�Ed��7�ȉ�
1/4-1/7=(7-3)/28�E�E�EX
(33)c=7
5/12-1/7=(35-12)/84=23/94<2/d�cd<188/23�E�E�Ed��8�ȉ�
23/94-1/8=(184-94)/(8*94)=90/(8*94)�E�E�EX
(3) a=2
1/2<4/b�E�E�Eb��7�ȉ�
(31)b=3
1/2-1/3=1/6<3/c�E�E�Ec��17�ȉ�
1/6-1/17=11/102<2/d�E�E�Ed<204/11�E�E�Ed��18�ȉ�
11/102�E�E�E�Ȃ�
1/6-1/16=10/(6*16)=5/48<2/d�E�E�Ed<96/5�E�E�Ed��19�ȉ��E�E�E�K������̂͂Ȃ�
1/6-1/15=1/10<2/d�E�E�Ed��19�ȉ�
�������Ȃ�
1/6-1/14=8/84=2/21<2/d�E�E�Ed��20�ȉ�
2/21-1/15=1/35
1/2+1/3+1/14+1/15+1/35
1/6-1/13=7/78<2/d�E�E�Ed<156/7�E�E�Ed��22�ȉ�
�����͂Ȃ�
1/6-1/12=1/12<2/d�E�E�Ed��23�ȉ�
1/12-1/21=1/28
1/2+1/3+1/12+1/21+1/28
1/12-1/20=1/30
1/2+1/3+1/12+1/20+1/30
1/12-1/18=1/36
1/2+1/3+1/12+1/18+1/36
1/12-1/16=1/48
1/2+1/3+1/12+1/16+1/48
1/12-1/15=1/60
1/2+1/3+1/12+1/15+1/60
1/12-1/14=1/84
1/2+1/3+1/12+1/14+1/84
1/12-1/13=1/156
1/2+1/3+1/12+1/13+1/156
1/6-1/11=5/66<2/d�cd<132/5�E�E�Ed��26�ȉ�
5/66-1/22=1/33
1/2+1/3+1/11+1/22+1/33
5/66-1/15=1/110
1/2+1/3+1/11+1/15+1/110
5/66-1/14=1/231
1/2+1/3;1/11+1/14+1/231
1/6-1/10=1/15<2/d�E�E�Ed��29�ȉ�
1/15-1/24=1/40
1/2+1/3+1/10+1/24+1/40
1/15-1/20=1/60
1/2+1/3+1/10+1/20+1/60
1/15-1/18=1/90
1/2+1/3+1/10+1/18+1/90
1/15-1/16=1/240
1/2+1/3+1/10+1/16+1/240
1/6-1/9=1/18<2/d�E�E�Ed��35�ȉ�
1/18=1/30=1/45
1/2+1/3+1/9+1/30+1/45
1/18-1/27=1/54
1/2+1/3+1/9+1/27+1/54
1/18-1/24=1/72
1/2+1/3+1/9+1/24+1/72
1/18-1/22=1/99
1/2+1/3+1/9+1/22+1/99
1/18-1/21=1/126
1/2+1/3+1/9+1/21+1/126
1/18-1/20=1/180
1/2+1/3+1/9+1/20+1/180
1/18-1/19=1/342
1/2+1/3+1/9+1/19+1/342
1/6-1/8=1/24<2/d�E�E�Ed��47�ȉ�
1/24-1/42=1/56
1/2+1/3+1/8+1/42+1/56
1/24-1/40=1/60
1/2+1/3+1/8+1/40+1/60
1/24-1/36=1/72
1/2+1/3+1/8+1/36+1/72
1/24-1/33=1/88
1/2+1/3+1/8+1/33+1/88
1/24-1/32=1/96
1/2+1/3+1/8+1/32+1/96
1/24-1/30=1/120
1/2+1/3+1/8+1/30+1/120
1/24-1/28=1/168
1/2+1/3+1/8+1/28+1/168
1/24-1/27=1/216
1/2+1/3+1/8+1/27+1/216
1/24-1/26=1/312
1/2+1/3+1/8+1/26+1/312
1/24-1/25=1/600
1/2+1/3+1/8+1/25+1/600
1/6-1/7=1/42<2/d�E�E�Ed��83�ȉ�
1/42-1/78=1/91
1/2+1/3+1/7+1/78+1/91
1/42-1/70=1/105
1/2+1/3+1/7+1/70+1/105
1/42-1/63=1/126
1/2+1/3+1/7+1/63+1/126
1/42-1/60=1/140
1/2+1/3+1/7+1/60+1/140
1/42-1/56=1/168
1/2+1/3+1/7+1/56+1/168
1/42-1/54=1/189
1/2+1/3+1/7+1/54+1/189
1/42-1/51=1/238
1/2+1/3+1/7+1/51+1/238
1/42-1/49=1/294
1/2+1/3+1/7+1/49+1/294
1/42-1/48=1/336
1/2+1/3+1/7+1/48+1/336
1/42-1/46=1/483
1/2+1/3+1/7+1/46+1/483
1/42-1/45=1/630
1/2+1/3+1/7+1/45+1/630
1/42-1/44=1/924
1/2+1/3+1/7+1/44+1/924
1/42-1/43=1/1806
1/2+1/3+1/7+1/43+1/1806
(32)b=4
1/2-1/4=1/4<3/c�E�E�Ec��11�ȉ�
1/4-1/11=7/44<2/d�E�E�Ed<88/7�E�E�Ed��12�ȉ�
7/44-1/12=5/66�E�E�EX
1/4-1/10=6/40=3/20<2/d�E�E�Ed<40/3�E�E�Ed��13�ȉ�
3/20-1/12=1/15
1/2+1/4+1/10+1/12+1/15
1/4-1/9=5/36<2/d�E�E�Ed��14�ȉ�
5/36-1/12=1/18
1/2+1/4+1/9+1/12+1/18
1/4-1/8=1/8<2/d�E�E�Ed��15�ȉ�
1/8-1/12=1/24
1/2+1/4+1/8+1/12+1/24
1/8-1/10=1/40
1/2+1/4+1/8+1/10+1/40
1/8-1/9=1/72
1/2+1/4+1/8+1/9+1/72
1/4-1/7=3/28<2/d�E�E�Ed��18�ȉ�
3/28-1/14=1/28
1/2+1/4+1/7+1/14+1/28
3/28-1/12=1/42
1/2+1/4+1/7+1/12+1/42
3/28-1/10=1/140
1/2+1/4+1/7+1/10+1/140
1/4-1/6=1/12<2/d�E�E�Ed��23�ȉ�
1/12-1/21=1/28
1/2+1/4+1/6+1/21+1/28
1/12-1/20=1/30
1/2+1/4+1/6+1/20+1/30
1/12-1/18=1/36
1/2+1/4+1/6+1/18+1/36
1/12-1/16=1/48
1/2+1/4+1/6+1/16+1/48
1/12-1/15=1/60
1/2+1/4+1/6+1/15+1/60
1/12-1/14=1/84
1/2+1/4+1/6+1/14+1/84
1/12-1/13=1/156
1/2+1/4+1/6+1/13+1/156
1/4-1/5=1/20<2/d�E�E�Ed��39�ȉ�
1/20-1/36=1/45
1/2+1/4+1/5+1/36+1/45
1/20-1/30=1/60
1/2+1/4+1/5+1/30+1/60
1/20-1/28=1/70
1/2+1/4+1/5+1/28+1/70
1/20-1/25=1/100
1/2+1/4+1/5+1/25+1/100
1/20-1/24=1/120
1/2+1/4+1/5+1/24+1/120
1/20-1/22=1/220
1/2+1/4+1/5+1/22+1/220
1/20-1/21=1/420
1/2+1/4+1/5+1/21+1/420
(33)b=5
1/2-1/5=3/10<3/c�E�E�Ec�͂X�ȉ�
3/10-1/9=17/90<2/d�cd<180/17�E�E�Ed��10�ȉ�
3/10-1/8=7/40<2/d�cd<80/7�E�E�Ed��11�ȉ�
3/10-1/7=11/70<2/d�cd<140/11�E�E�Ed��12�ȉ�
3/10-1/6=4/30=2/15<2/d�E�E�Ed��14�ȉ�
2/15-1/12=1/20
1/2+1/5+1/6+1/12+1/20
2/15-1/10=1/30
1/2+1/5+1/6+1/10+1/30
2/15-1/9=1/45
1/2+1/5+1/6+1/9+1/45
2/15-1/8=1/120
1/2+1/5+1/6+1/8+1/120
(34)b=6
1/2-1/6=1/3<3/c�E�E�Ec��8�ȉ�
1/3-1/8=5/24<2/d�E�E�Ed�͂X�ȉ�
�K������̂Ȃ�
1/3-1/7=4/21<2/d�E�E�Ed��10�ȉ�
�K������̂Ȃ�
(35)
1/2-1/7=5/14<3/c�cc<42/5�E�E�Ec��8�ȉ�
5/14-1/8=(40-14)/(8*14)=13/56<2/d�cd<112/13�E�E�Ed��8�ȉ��E�E�E�Ȃ�
PC�ł�
1/2+1/3+�^�C�v�E�E�E45��
1/2+1/4+�^�C�v�E�E�E22��
1/2+1/5+�^�C�v4��
1/3+1/4+1/5+1/6+1/20�E�E�E1��
�S����72��
So�c��̂��̂ł��ׂĂ̂͂�
�u�X���[�N�}���v 03/07�@�@ 21��21���@ ��M �X�V 3/30
NO5�u��x�Ђ����v 03/16 19��59���@ ��M �X�V 3/30
��452��̉�����̉F
�m�P�ʕ����n
1��4�̒P�ʕ����ɕ���������@�͎���14�ʂ�D(��)
1=(1/2)+(1/3)+(1/7)+(1/42),
=(1/2)+(1/3)+(1/8)+(1/24),
=(1/2)+(1/3)+(1/9)+(1/18),
=(1/2)+(1/3)+(1/10)+(1/15),
=(1/2)+(1/3)+(1/12)+(1/12),
=(1/2)+(1/4)+(1/5)+(1/20),
=(1/2)+(1/4)+(1/6)+(1/12),
=(1/2)+(1/4)+(1/8)+(1/8),
=(1/2)+(1/5)+(1/5)+(1/10),
=(1/2)+(1/6)+(1/6)+(1/6),
=(1/3)+(1/3)+(1/4)+(1/12),
=(1/3)+(1/3)+(1/6)+(1/6),
=(1/3)+(1/4)+(1/4)+(1/6),
=(1/4)+(1/4)+(1/4)+(1/4).
�܂��C1��4�̒P�ʕ����ɁC�P�ʕ�����������\�����@�͎���6�ʂ�D
1=(1/2)+(1/3)+(1/7)+(1/42),
=(1/2)+(1/3)+(1/8)+(1/24),
=(1/2)+(1/3)+(1/9)+(1/18),
=(1/2)+(1/3)+(1/10)+(1/15),
=(1/2)+(1/4)+(1/5)+(1/20),
=(1/2)+(1/4)+(1/6)+(1/12).
1=(1/a)+(1/b)+(1/c)+(1/d), a��b��c��d
�����悤�Ȑ�����a,b,c,d�̑g(a,b,c,d)��
���ׂċ��߂�悢�D
1-(1/a)=(1/b)+(1/c)+(1/d)>0 ���C2��a.
(4/a)��(1/a)+(1/b)+(1/c)+(1/d)=1 ���Ca��4.
����āC2��a��4.
1-(1/a)-(1/b)=(1/c)+(1/d)>0 ���Cfloor(1/(1-(1/a)))+1��b.
(3/b)��(1/b)+(1/c)+(1/d)=1-(1/a) ���, b��floor(3/(1-(1/a))).
����āCmax(a,floor(1/(1-(1/a)))+1)��b��floor(3/(1-(1/a))) ---(1)
1-(1/a)-(1/b)-(1/c)=(1/d)>0 ���Cfloor(1/(1-(1/a)-(1/b)))+1��c.
(2/c)��(1/c)+(1/d)=1-(1/a)-(1/b) ���, c��floor(2/(1-(1/a)-(1/b))).
����āCmax(b,floor(1/(1-(1/a)-(1/b)))+1)��c��floor(2/(1-(1/a)-(1/b))) ---(2)
�Ea=2�̏ꍇ�F
(1)���C3��b��6.
(a,b)=(2,3)�̂Ƃ��C(2)���C7��c��12.
���̂����C(d)=1/(1-(1/a)-(1/b)-(1/c))�� 7 �ȏ�̐����ƂȂ�悤��(a,b,c)�́C
(a,b,c)=(2,3,7),(2,3,8),(2,3,9),(2,3,10),(2,3,12).
(a,b)=(2,4)�̂Ƃ��C(2)���C5��c��8.
���̂����C(d)=1/(1-(1/a)-(1/b)-(1/c))�� 5 �ȏ�̐����ƂȂ�悤��(a,b,c)�́C
(a,b,c)=(2,4,5),(2,4,6),(2,4,8).
(a,b)=(2,5)�̂Ƃ��C(2)���C5��c��6.
���̂����C(d)=1/(1-(1/a)-(1/b)-(1/c))�� 5 �ȏ�̐����ƂȂ�悤��(a,b,c)�́C
(a,b,c)=(2,5,5)�̂�.
(a,b)=(2,6)�̂Ƃ��C(2)���Cc=6.
���̂Ƃ��C(d)=1/(1-(1/a)+(1/b)+(1/c))=6 �ƂȂ�D
�Ea=3�̏ꍇ�F
(1)���C3��b��4.
(a,b)=(3,3)�̂Ƃ��C(2)���C4��c��6.
���̂����C(d)=1/(1-(1/a)-(1/b)-(1/c))�� 4 �ȏ�̐����ƂȂ�悤��(a,b,c)�́C
(a,b,c)=(3,3,4),(3,3,6).
(a,b)=(3,4)�̂Ƃ��C(2)���Cc=4.
���̂Ƃ��C(d)=1/(1-(1/a)-(1/b)-(1/c))=6 �ƂȂ�D
�Ea=4�̏ꍇ�F
(1)���Cb=4.
(a,b)=(4,4)�̂Ƃ��C(2)���Cc=4.
���̂Ƃ��C(d)=1/(1-(1/a)-(1/b)-(1/c))=4 �ƂȂ�D
�ȏ���C����14�g�����ƂȂ�D
(a,b,c,d)
=(2,3,7,42),(2,3,8,24),(2,3,9,18),(2,3,10,15),(2,3,12,12),
(2,4,5,20),(2,4,6,12),(2,4,8,8),(2,5,5,10),(2,6,6,6),
(3,3,4,12),(3,3,6,6),(3,4,4,6),(4,4,4,4).
[�]�͖��]
1=(1/a)+(1/b)+(1/c)+(1/d)+(1/e),
a<b<c<d<e
�����悤�Ȑ�����a,b,c,d,e�̑g(a,b,c,d,e)�̑�����
������悢�D���̑g�̑����� 72 (��)
1-(1/a)=(1/b)+(1/c)+(1/d)+(1/e)>0 �����
(5/a)>(1/a)+(1/b)+(1/c)+(1/d)+(1/e)=1 ���C
2��a��4.
1-(1/a)-(1/b)=(1/c)+(1/d)+(1/e)>0 �����
(4/b)>(1/b)+(1/c)+(1/d)+(1/e)=1-(1/a) ���,
max(a+1,floor(1/(1-1/a))+1)��b��ceil(4/(1-1/a))-1.
1-(1/a)-(1/b)-(1/c)=(1/d)+(1/e)>0 �����
(3/c)>(1/c)+(1/d)+(1/e)=1-(1/a)-(1/b) ���,
max(b+1,floor(1/(1-(1/a)-(1/b)))+1)��c��ceil(3/(1-(1/a)-(1/b)))-1.
1-(1/a)-(1/b)-(1/c)-(1/d)=(1/e)>0 �����
(2/d)>(1/d)+(1/e)=1-(1/a)-(1/b)-(1/c) ���,
max(c+1,floor(1/(1-(1/a)-(1/b)-(1/c)))+1)��d��ceil(2/(1-(1/a)-(1/b)-(1/c)))-1.
�����ŁC
e=1/(1-(1/a)-(1/b)-(1/c)-(1/d))
�Ƃ����Ƃ��Ce���������ۂ����`�F�b�N����悢�D
�ȏ��maxima�Ōv�Z������v���O�������C���ł��D
count:0$
for a:2 thru 4 do (
for b:max(a+1,floor(1/(1-1/a))+1) thru ceiling(4/(1-1/a))-1 do ( for c:max(b+1,floor(1/(1-1/a-1/b))+1) thru ceiling(3/(1-1/a-1/b))-1 do ( for d:max(c+1,floor(1/(1-1/a-1/b-1/c))+1) thru ceiling(2/(1-1/a-1/b-1/c))-1 do ( s:[a,b,c,d,1/(1-1/a-1/b-1/c-1/d)],
if floor(s[5])+floor(-s[5])=0 then (count:count+1,print(count,":",s))
))));
���̃v���O�����̎��s���� �� https://fpseries.exblog.jp/33549829/
OEIS�ɂ́C1��n�̒P�ʕ����ɒP�ʕ�������������@�̑��� a(n)
�̒l���f�ڂ���Ă��܂��ˁD
���̐����グ���́C���Ȃ�̓��̂悤�ł��D
a(9)�ȍ~�̒l�͖��o�^�ł��D
�P�ʕ��������̕��@�������ɂ��邱�Ƃ́C���̓���������킩��܂��D
2�ȏ�̔C�ӂ̐��� n, m �ɑ��āC
(1/n) = 1/(n+1) + 1/(n+1)^2 + 1/(n+1)^3 + �c + 1/(n+1)^m + 1/(n*(n+1)^m)�D
���̓�������C(1/n)�́C(m+1)�̈قȂ�P�ʕ����̘a�ŕ\����邱�Ƃ��킩��܂��D
�܂��C���̓���������P�ʕ��������̕��@�������ɂ��邱�Ƃ��킩��܂��D
(1/n) = 1/(n*(m+1)!) + ��[k=1�`m]1/(n*(k+1)!/k).
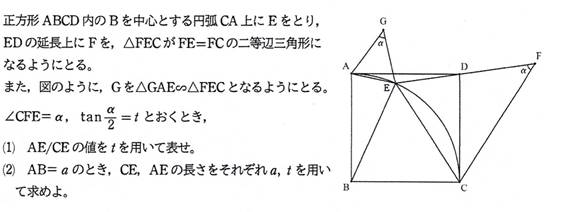
[�lj���� 1]
(1)
(AE/CE)=(1-t)/��2 (��)
(2) CE=(2*a)/��(5-4*t+t^2), AE=(1-t)*a*��(2/(5-4*t+t^2)) (��)
BC=x�Ƃ����D
����CE�̒��_�� M �Ƃ��C��CBM=�� �Ƃ����D
MB��CE�CMF��CE�ł��邩��C3�_ B,M,F �͓��꒼����ɂ��邱�Ƃ��킩��D
��BFC=(��/2) �ł���D
��BCF�ɐ����藝���g���āC
FC=sin(��)*(x/sin(��/2)) ---(1)
��DCF=��BCF-(��/2)=(��-(��+��/2))-(��/2)=(��/2)-(��+��/2).
��CDF=��-(��DCF+��CFD)=(��/2+��-��/2).
��CDF�ɐ����藝���g���āC
FC=sin(��/2+��-��/2)*(x/sin(��)), ���Ȃ킿�C
FC=cos(��-��/2)*(x/sin(��)) ---(2)
(1),(2)���C
sin(��)*(x/sin(��/2))=cos(��-��/2)*(x/sin(��)).
����āC
sin(��)*sin(��)=sin(��/2)*cos(��-��/2).
���ӂ�sin(��/2)�Ŋ����āC
2*cos(��/2)*sin(��)=cos(��-��/2).
����āC
2*cos(��/2)*sin(��)=cos(��)*cos(��/2)+sin(��)*sin(��/2).
���ӂ� cos(��/2)*sin(��) �Ŋ����āC
2=cot(��)+tan(��/2) ---(3)
����AE�̒��_�� N �Ƃ���D
AE=2*AN=2*BA*sin(��ABN)=2*x*sin((��/2-2*��)/2)
=2*x*sin(��/4-��)=(2^(1/2))*x*(cos(��)-sin(��)).
CE=2*x*sin(��).
����āC
(AE/CE)
=(2^(-1/2))*(cot(��)-1)
=(2-tan(��/2)-1)/��2 (��(3)���Ccot(��)=2-tan(��/2))
=(1-tan(��/2))/��2
=(1-t)/��2.
(sin(��))^2
=1-(cos(��))^2
=1-1/(1+(tan(��))^2)
=(tan(��))^2/(1+(tan(��))^2)
=1/((cot(��))^2+1)
=1/((2-t)^2+1)
=1/(5-4*t+t^2).
����āC
sin(��)=1/��(5-4*t+t^2).
CE=2*x*sin(��)=(2*a)/��(5-4*t+t^2).
AE=((1-t)/��2)*CE=(1-t)*a*��(2/(5-4*t+t^2)).
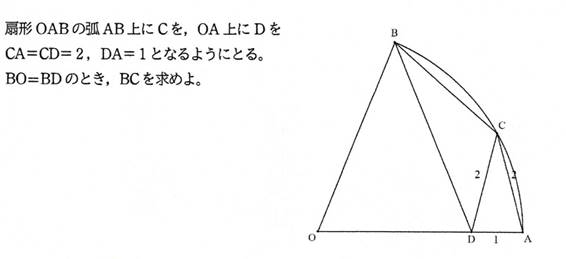
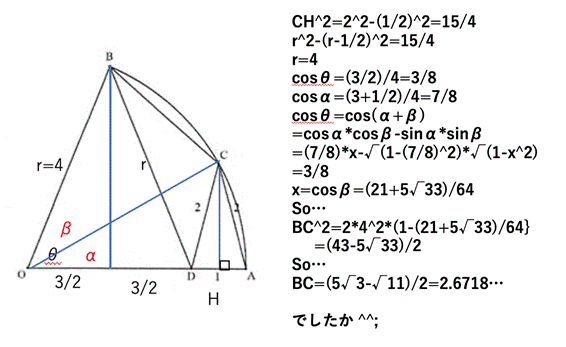
[�lj���� 2]
BC=(1/2)*(5*3^(1/2)-11^(1/2))
(��)�D
��OAC �� ��CAD �ł���D
(�܂����炩�ɁC��OAC=��CAD.
OA=OC�ł��邱�Ƃ���C��OAC=��OCA.
CA=CD�ł��邱�Ƃ���C��CAD=��CDA.
����āC��OCA=��CDA. )
OA=x�Ƃ����D
��OAC �� ��CAD �ł��邱�Ƃ���C
2:x=1:2. ����āCx=4. OD=OA-AD=4-1=3.
��AOC=2*���C��AOB=2*�� �Ƃ����D
sin(��)=(1/2)*(AC)/(OA)=1/x=(1/4).
cos(��)=(1-(sin(��))^2)^(1/2)=(1/4)*15^(1/2).
cos(2*��)=(1/2)*(OD)/(OB)=(1/2)*(3)/x=(3/8).
cos(��)=((1+cos(2*��))/2)^(1/2)=(1/4)*11^(1/2).
sin(��)=((1-cos(2*��))/2)^(1/2)=(1/4)*5^(1/2).
����āC
BC=2*(OB)*sin(��-��)
=2*4*(sin(��)*cos(��)-cos(��)*sin(��))
=(1/2)*(5*3^(1/2)-11^(1/2)).
(�ȏ�)
�����̗���F�ȉ��̏�肪�Ƃ��������܂��B����Ƃ��ĉ����̋K���������o�����Ƃ��čl���܂������A�f�O��������ł��B���������B��
OEIS�ɂ́C1��n�̒P�ʕ����ɒP�ʕ�������������@�̑��� a(n)
�̒l���f�ڂ���Ă��܂��ˁD
���̐����グ���́C���Ȃ�̓��̂悤�ł��D
a(9)�ȍ~�̒l�͖��o�^�ł��D
NO6�ukasama�v
03/21
01��26���@�@ ��M �X�V 3/30
���ꂽ������
NO7�u��ӂ����̂炢��������v 03/23 16��05�� ��M �X�V 3/30 �@
�@�@���ꂽ������
NO7�u�l�c�����v �@�@04/30 �@�@�@06��16�� �@�@��M �X�V 4/30 �@
���ꂽ������
���R�����g�F���̂T�̏ꍇ�̃f�[�^�����߂Ă݂܂����B���D
�u���̗���v
�X�V 3/30

�Q�l�F���͉ߋ�����291��̖���Ɠ����ł����B
