令和7年4月27日
 [流れ星]
[流れ星]
第453回数学的な連続応募解答
<解答募集期間:3月30日〜4月27日>
[ヘロンの三角形]
高校で三角形の面積を求めるのに、ヘロンの公式を教えています。
そこで、3辺の長さとその面積がともに整数となる三角形をヘロンの三角形と言います。
問題1方程式:![]() はペル方程式の1つです。
はペル方程式の1つです。
この方程式の負でない整数解(x、y)の特殊解または、一般解を求めてください。
問題2:3辺の長さが3、4,5の三角形の面積は6です。このような3辺の長さが連続する3つの自然数で、ヘロンの三角形を幾つか求めてください。
参考文献 日本の数学 何題解けますか?[上] 深川英俊 著 森北出版社
楽しむ初等数学 松田康雄 九州大学出版会
追加問題(出題者は「ジョーカー」) 新作シリーズ
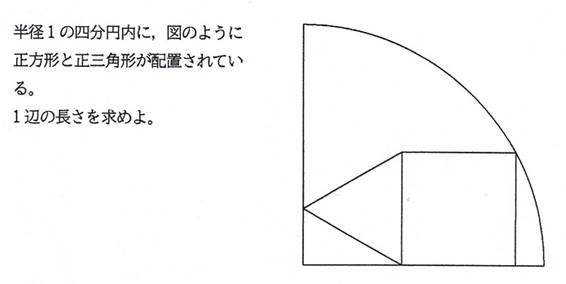
四分円内の正方形と正三角形の1辺について『1』
問題1 シリーズ1問目
正方形と正三角形の1辺が等しいとき(辺を共有する),
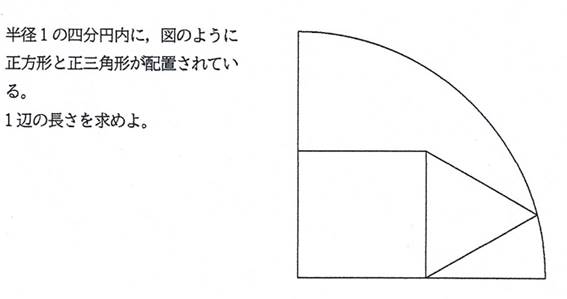
問題2 シリーズ2問目
正方形と正三角形の1辺が等しいとき(辺を共有する),
NO1「ジョーカー」 03/30
11時24分 受信 更新 4/27
寄せられた解答です
NO2「スモークマン」 04/03 23時06分
受信 更新 4/27
問題1
2^2=3*1^2+1
7^2=3*4^2+1
x^2=3y^2+1
x^2-2^2=(x-2)(x+2)
=3y^2-3=3(y+1)(y-1)
x+2=3(y-1)
x-2=y+1
2x=4y-2
x=2y-1
(2y-1)^2=3y^2+1
y^2-4y=0…y=4,x=7
x^2-7^2=3y^2-48=3(y^2-16)
x+7=3(y-4)
x-7=y+4
2x=4y-8
x=2y-4
(2y-4)^2=3y^2+1
y^2-16y+15=(y-1)(y-15)
y=15,x=26
(2y-4)^2=3y^2+1
x^2-26^2=3y^2-26^2+1=3(y^2-225)
(x-26)(x+26)=3(y-15)(y+15)
x+26=3(y-15)
x-26=y+15
2x=4y-30
x=2y-15
(2y-15)^2=3y^2+1
y^2-60y+224=(y-6)(y-56)=0
x>0…y=56
so…x=2y-p
(2y-p)^2=3y^2+1
y^2-4py+p^2-1=0
(y-2p)^2=3p^2+1
y=2p±√(3p^2+1)
(y,x)=(0,1)=(2*1+√(3*1^2+1)=4,2*4-1=7)=
(2,1),(4,15),(15,4)
のように次々と求められる...
漸化式がわかればいずれまた...Orz
問題2
k-1,k,k+1
s=k
√(3k/2(3k/2-k)(3k/2-k+1)(3k/2-k-1)
=(1/4)√(3k^2(k^2-4))=整数 m
So…
√(3k^2(k^2-4))=4m^2
So…k=2x
3(x^2-1)=平方数
x^2-1=3z^2
これは、x^2=3y^2+1 という問題1の解となる。
具体的な数値はいずれまた
NO3「よふかしのつらいおじさん」04/04 9時24分 受信 更新 4/27
寄せされた解答です
<コメント:今回のペル方程式は面白かったです。いままで知りませんでした。追加問題は計算が今までになく少なかったので逆に驚きました>
NO4「三角定規」 04/13 16時15分 受信 更新 4/27
寄せされた解答です
<コメント:今回,問題1の <ペル方程式> を問題2の <ヘロンの三角形> で使うと思うのですが,私の解はそうなっていません。いろいろ考えてはみたのですが,うまくたどり着かないので,そのまま送ることにしました。>
NO5「二度漬け白菜」 04/19 14時48分 受信 更新 4/27
第453回の応募問題の解答:
[問題1]
x^2=3*y^2+1 のすべての非負整数解
(x,y) は,
(x,y)=(((2+√3)^n+(2-√3)^n)/2,
((2+√3)^n-(2-√3)^n)/(2*√3))
(nは0以上の任意の整数)
で与えられる.(答)
方程式:x^2=3*y^2+1 のすべての非負整数解(x,y)たちについて,
x+y*√3の値が小さい順に並べたものを,
(x[0],y[0]),(x[1],y[1]),(x[2],y[2]),(x[3],y[3]),…,(x[n],y[n]),…
とする.このとき,
(x[n],y[n])=(((2+√3)^n+(2-√3)^n)/2, ((2+√3)^n-(2-√3)^n)/(2*√3))
---(★)
となる.
x^2=3*y^2+1 の非負整数解を,x+y*√3の値が小さい順に10個列挙すると,
(x,y)=(1,0),(2,1),(7, 4), (26, 15), (97,
56), (362, 209), (1351, 780), (5042, 2911), (18817, 10864), (70226, 40545).
(★)について:
方程式:x^2=3*y^2+1 の正整数解(x,y)のうち,x+y*√3の値が最小となるのは,
(x,y)=(2,1)のとき.
ε=2+√3とおく.
任意の正整数 n に対して,
ε^n=x[n]+y[n]*√3
で定まるような(x,y)=(x[n],y[n])が,方程式 x^2=3*y^2+1 のすべての
正整数解となります.このことの証明は下記のサイトに詳しく書いてあります.
https://wkmath.org/pell-f.html#t-sol
(2+√3)^n=x[n]+y[n]*√3 および
(2-√3)^n=x[n]-y[n]*√3 であることから,
x[n]=((2+√3)^n+(2-√3)^n)/2,
y[n]=((2+√3)^n-(2-√3)^n)/(2*√3).
[問題2]
与えられた条件を満たすような三角形は,その3辺の長さが,
2*x[n]-1, 2*x[n], 2*x[n]+1 (x[n]=((2+√3)^n+(2-√3)^n)/2, n≧1)
で与えられる三角形である.
面積が小さい順に 5 個列挙すると,
(3,4,5) 面積 6
(13,14,15) 面積 84
(51,52,53) 面積 1170
(193,194,195) 面積 16296
(723,724,725) 面積 226974. (答)
条件を満たすような三角形の3辺の長さを,
(a-1), a, (a+1) (ただし,aは3以上の整数),
その面積を S とおく.
ヘロンの公式より,
S^2=((3*a)/2)*((3*a)/2-(a-1))*((3*a)/2-a)*((3*a)/2-(a+1)).
よって,
16*S^2=3*a^2*(a^2-4).
この式からaは偶数であることがわかる.
a=2*x (xは2以上の整数)とおいて,16*S^2=3*a^2*(a^2-4)に代入し整理すると,
S^2=3*x^2*(x^2-1).
よって,S=x*(3*(x^2-1))^(1/2).
この式から,3*(x^2-1)は平方数であることがわかる.
3*(x^2-1)=z^2 (zは3以上の整数) とおける.
この式からz^2は3の倍数,よって,zは3の倍数であることがわかる.
z=3*y (yは1以上の整数)とおいて,3*(x^2-1)=z^2に代入し整理すると,
x^2=3*y^2+1.
この方程式の解は[問題1]で示した(★)で与えられる.
このとき,
S=3*x*y=3*x[n]*y[n]=((√3)/4)*((7+4*√3)^n-(7-4*√3)^n) (ただし,n≧1).
[追加問題1]
一辺の長さは,2/(11+4*3^(1/2))^(1/2)
(答)
正方形の一辺の長さを s とおくと,
((s/2)*3^(1/2)+s)^2+s^2=1^2.
よって,s=2/(11+4*3^(1/2))^(1/2).
[追加問題2]
一辺の長さは,
(1/2)*(6^(1/2)-2^(1/2))(答)
正方形の一辺の長さを s とおくと,
((s/2)*3^(1/2)+s)^2+(s/2)^2=1^2.
よって,s=(1/2)*(6^(1/2)-2^(1/2)).
-------------------------------------------
ヘロンの三角形のうち,3辺の長さが連続する整数であるようなものを
「ブラーマグプタの三角形」と呼ぶようですね.
この「ブラーマグプタの三角形」においては,内接円の半径rも整数であり,
r=y[n]が成り立っているということも面白いです.
(以上)
<水の流れ:知らないことを知ることができ感謝します>
NO6「浜田明巳」 04/25 20時31分
受信 更新 4/27
問題1・2の寄せされた解答です
追加問題1・2の寄せされた解答です
<水の流れ:浜田さんはお久しぶりの応募で,調べてみたら、第383回 令和2年2月19日以来でした。応募に感謝します。>
「水の流れ」 更新 4/27



参考 すでにヘロンの三角形は以前に出題していました。
