�ߘa�V�N�X���P�S��
 [���ꐯ]
[���ꐯ]
�@�@��458�����w�I�ȘA�������
�@�@�@����W���ԁF8��17���`9��14����
�m���̒l��n
�@
���@
�i�P�j��![]() �̑�����,�O���t�̊T�`��`���B
�̑�����,�O���t�̊T�`��`���B
�i�Q�j����![]() �����̂S�̏��������Ȃ��瓮���Ƃ�,
�����̂S�̏��������Ȃ��瓮���Ƃ�,![]() �̂Ƃ蓾��l�͈̔͂����߂�B
�̂Ƃ蓾��l�͈̔͂����߂�B
�@�@![]() �E�E�E�@
�E�E�E�@
�@�@![]() �E�E�E�A
�E�E�E�A
�@�@![]() �E�E�E�B
�E�E�E�B
�@�@![]() �E�E�E�C
�E�E�E�C
�@�@
�@�o�T�@2025�N�����Ȋw��w�i���H�n�j�̉���
�lj�����i�o��҂́u�W���[�J�[�v�j�@�V��V���[�Y
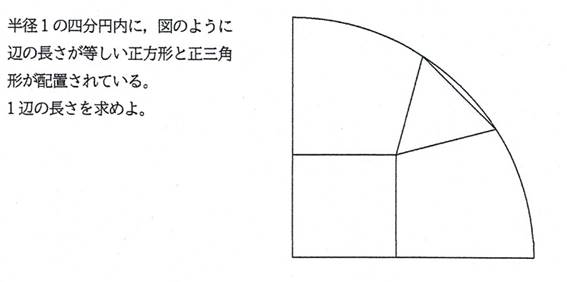
�l���~���̐����`�Ɛ��O�p�`��1�ӂɂ��āw�Q�x�@
���P�@�@�V���[�Y�R���
�����`�Ɛ��O�p�`��1�ӂ��������Ƃ�(�ӂ����L���Ȃ�),
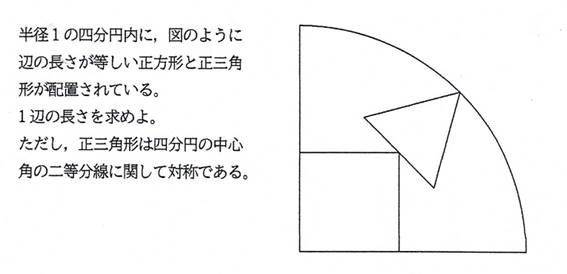
���Q�@�V���[�Y�S���
�����`�Ɛ��O�p�`��1�ӂ��������Ƃ�(�ӂ����L���Ȃ�),
NO1�u�W���[�J�[�v �@ 08/17�@�@ 17��13�� ��M �X�V 9/14
��ꂽ������
NO2�u�l�c�����v�@�@�@ 08/18 11��29���@ ��M �X�V 9/14
��ꂽ������
NO3�u��ӂ����̂炢��������v 08/20 17��43�� ��M �X�V 9/14
��ꂽ������
NO4�u�O�p��K�v
08/25
22��33���@ ��M �X�V 9/14
��ꂽ������
NO5�u�X���[�N�}���v 08/28 00��27���@ ��M �X�V 9/14
�lj����P�C�Q
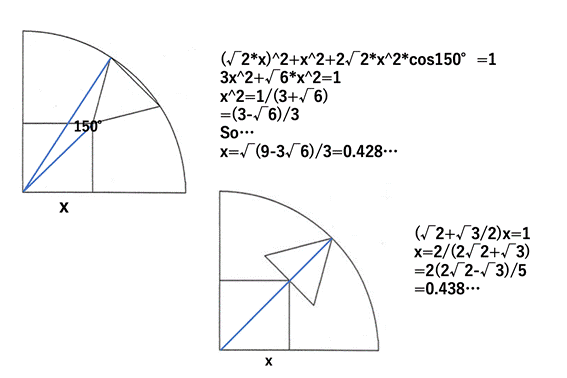
NO6�ukasama�v
08/29
01��10���@�@ ��M �X�V 9/14
��ꂽ������
NO7�u��x�Ђ����v 09/06 15��38���@ ��M �X�V 9/14
[���]
(1)
f(-t)=-f(t)�ł��邩��Cy=f(t)�̃O���t�͌��_�Ώ́D
(d/dt)f(t)=(3-t)*(3+t)/t^4,
(d^2/dt^2)f(t)=2*(t-3*2^(1/2))*(t+3*2^(1/2))/t^5,
lim[t��+0]f(t)=-���Clim[t����]f(t)=+0.
�ɑ�_:(3,2/9),
�ɏ��_:(-3,-2/9),
�ϋȓ_:(3*2^(1/2),(5/36)*2^(1/2)),(-3*2^(1/2),-(5/36)*2^(1/2)).
t>0�ł�f(t)�̑����ƌ��_�Ώ̐����l�����āCy=f(t)�̃O���t��
�}�̂悤�ɂȂ�D
�}�� https://fpseries.exblog.jp/iv/detail/?s=33770748&i=202509%2F05%2F59%2Fe0454859_10462766.jpg
(2) x<-3 ����� -3^(1/2)<x<-(3/2) (��)
{�A�C�B�C�C}
��{(y^2-3)/y^3=(x^2-3)/x^3,
(z^2-3)/z^3=(y^2-3)/y^3} ��{f(x)=f(y)=f(z)}
�ł���D����āC
(x,y,z��4�̏���:�@�C�A�C�B�C�C���ɖ�����)
��
(x,y,z�� t�̕�����f(t)=k (k�͎���) �̈قȂ�3�̎�����
���� x<y<z).
�O���t���C����k���ω�����Ƃ��Ct�̕����� f(t)=k �́C
���X3�̉����������Ȃ����Ƃ��킩��D
f(t)=k�����傤��3�̉������悤��k�̒l�͈̔͂́C
(-2/9)<k<0 ����� 0<k<(2/9)---���ł���D
f(t)=(2/9)�ƂȂ�悤��t�̂����Ct=3�ȊO�̂��̂́Ct=-(3/2).
(��f(t)=(2/9)��9*(t^2-3)=2*t^3��2*(t-3)^2*(t+3/2)=0.)
k�����͈̔͂��Ƃ��́Cf(t)=k��3�̉��̂����̍ŏ��̂��̂�
x�ł��邩��C�O���t���Cx�̎�蓾��l�͈̔͂́C
x<-3 �����
-3^(1/2)<x<-(3/2)�@(��)
[�lj����1]
��ӂ̒����́C(1/3)*(9-3*6^(1/2))^(1/2)
(��)
��ӂ̒�����s�Ƃ���ƁC
(s*2^(1/2)+s*(1/2)*3^(1/2))^2+(s/2)^2 =
1^2.
����āCs=(1/3)*(9-3*6^(1/2))^(1/2).
[�lj����2]
��ӂ̒����́C(2/5)*(2*2^(1/2)-3^(1/2))
(��)
��ӂ̒�����t�Ƃ���ƁC
t*2^(1/2)+t*(1/2)*3^(1/2)=1.
����āCt=(2/5)*(2*2^(1/2)-3^(1/2)).
(�ȏ�)
�����̗��ꁄ�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�X�V�@9��14��
�i�P�j�@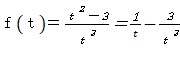 �@��f(-t)=-f(t)������ł���B
�@��f(-t)=-f(t)������ł���B
����āA�O���t�͌��_�Ώۂł���B�܂�,�@
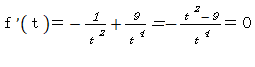 �@���,�@
�@���,�@![]() �@
�@
�����,![]()
�ł��邩��,f(t)�̑����\�͎��̂悤�ɂȂ�B

�����,f(t)�̃O���t�̊T�`�͈ȉ��̂ł���B
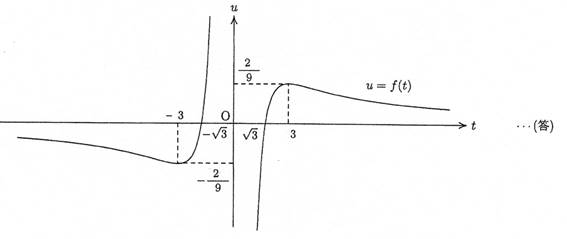
�i�Q�j![]() �E�E�E�@
�E�E�E�@
�@�@![]() �E�E�E�A
�E�E�E�A
�@�@![]() �E�E�E�B
�E�E�E�B
�@�@![]() �E�E�E�C
�E�E�E�C
�����ׂĖ���������y,z�����݂��邱�Ƃł���B
�A���,![]() �ł���B���̂��ƂŇB��
�ł���B���̂��ƂŇB��
�@![]() �@,�@
�@,�@ �@����,
�@����,
��(��)��f(��)�ƂȂ�B���l�ɂ��ćC�͂�(��)��f(��)�ƂȂ邩��A
�B���C��, ��(��)��f(��)��f(��)�ƂȂ�B
����Ƈ@���狁�߂������, ��(��)��f(��)��f(z)=k �����قȂ����x,y,z�����݂���悤�Ȃ��͈̔͂��l���Ă݂�B
���̂��߂ɂ͂��̕�����f(t)�������قȂ�R�̎������������Ƃł���B
�i�P�j�̃O���t����,![]() �ł���A����u�����i���j��u�����̂R�̌�_�̂����ł������̂��̂ɑΉ�����E
�ł���A����u�����i���j��u�����̂R�̌�_�̂����ł������̂��̂ɑΉ�����E
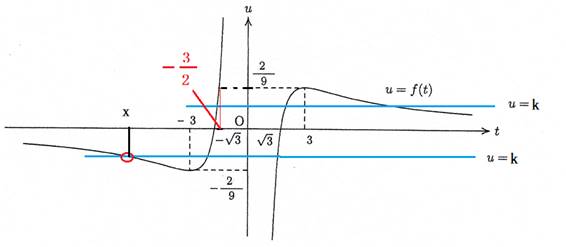
������,�@![]() �ƂȂ�Ƃ������߂��,
�ƂȂ�Ƃ������߂��,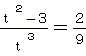 �@,�@
�@,�@
���,�i���|�R�j�Q�i�Q���{�R�j���O�@�ƂȂ邩��, ![]() �ł���B
�ł���B
�i�P�j�ŕ`�����������i���j�̃O���t���狁�߂������,
�@�@![]() �ł���B
�ł���B
�ȏ���,���̂Ƃ蓾��l�͈̔͂�, �@![]() ��
��
�Q�l�@���̂Ƃ蓾��l�͈̔͂�, �@![]() ��
��
�@�@�@���̂Ƃ蓾��l�͈̔͂�, �@![]()
