�ߘa�W�N�P���S��
 [���ꐯ]
[���ꐯ]
�@�@��462�����w�I�ȘA�������
�@�@�@����W���ԁF12��7���`1��4����
�m�ŒZ�����n
�ߘa�W�N���߁i�Ђ̂����܁j�����܂��Ă��߂łƂ��������܂��B
��N�܂ł̂�����ɐ[�����Ӑ\���グ�܂��B
���N���������������ڎ���܂��悤��낵�����肢�������܂��B
���
�����͂��ׂĐ��̐��Ƃ���B
���Q�{���Q�{�������S�X
���Q�{���Q�{�������U�S
���Q�{���Q�{�������Q�T
��,y,������̂R�������Ƃ�,���{���{���̒l�����߂�B
����@�Ɏg���Q�l�}�@�_P���t�F���}�[�_�Ƃ����B
�@�������A��ABC�͉s�p�O�p�`�̂Ƃ��̐}
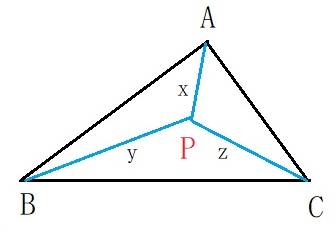
���@�s�p�O�p�`�`�a�b�ɂ�����,AB=c,BC=a,CA=b,�ʐς�S�Ƃ���B��ABC�̓����ɓ_P���Ƃ�,AP�{BP+CP���ŏ��ɂ���_P�Ƃ���B���̂Ƃ���AP+BP+CP�̒l��a,b,c,S�ŕ\���B
�lj�����i�o��҂́u�W���[�J�[�v�j�@�V��V���[�Y
�l���~���̐����`�Ɛ��O�p�`��1�ӂɂ��āw�R�x�@
���P�@�@�V���[�Y�R���
�����`�Ɛ��O�p�`��1�ӂ��قȂ�i������),
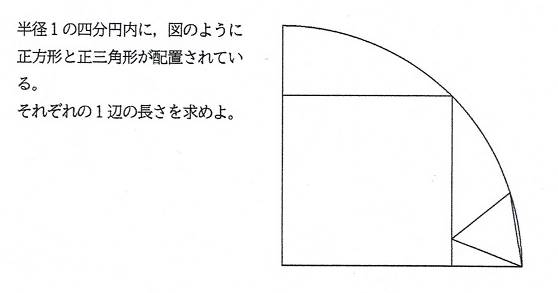
���Q�@�V���[�Y�S���
�����`�Ɛ��O�p�`��1�ӂ��قȂ�i������),
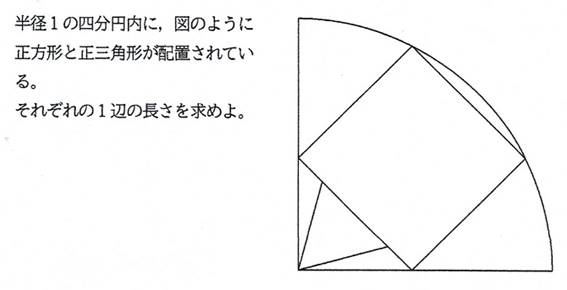
NO1�u�W���[�J�[�v �@ 12/07�@�@ 20��14�� ��M �X�V 1/4
�����������
NO2�u�X���[�N�}���v 12/07 22��13���@ ��M �X�V 1/4
���悢��t��...(���V���Z���Ȃ����Ƃ���̂悤�ł��� ^^)
�P�N���{���ɑ����߂����Ⴂ�܂�...
���N���y���܂��Ă��������܂������ƂɌ��\���グ�܂��B
���N���y���݂ɂ��Ă���܂��B
���Ƒ����ł����A�ǂ��N�����}�����������܂� Orz〜v
��� �ŒZ����
sin60��*(xy+yz+zx)=2��(10*3*2*5)=20��3
xy+yz+zx=40
2(x^2+y^2+z^2)=49+64+25-40=98
x^2+y^2+z^2=49
(x+y+z)^2=x^2+y^2+z^2+2(xy+yz+zx)=49+80=129
x+y+z=��129
���
��̎�������������...
a^2=x^2+y^2+xy
b^2=y^2+z^2+yz
c^2=z^2*x^2+zx
4S=(xy+yz+zx)��3
x^2+y^2+z^2=a^2+b^2+c^2-4S/��3
So�c
AP+BP+CP=��(a^2+b^2+c^2-4S/��3+2S/��3)
=��(a^2+b^2+c^2-2S/��3)


NO3�u��ӂ����̂炢��������v 12/09 22��26�� ��M �X�V 1/4
��ꂽ������
����̖��́A�O��̑Q�����̖���2�߁icos�̔��p�̌����̂��́j�̖����������o�ł��܂����B
�t�F���}�[�_�Ƃ����P��͒m��܂���ł������A
�O�p�`�̊e���_�܂ł̋����̘a���ŏ��ɂȂ�_�́A
��APB����BPC����CPA��120�x�̓_P�Ƃ����m���͂���܂����B
�����g��Ȃ��ƌv�Z����ς����Ȃ̂ŁA������܂����B
NO4�u�O�p��K�v
12/13
19��39���@ ��M �X�V 1/4
��ꂽ������
�t�F���}�[�_�C�m��قǂɋ��������s�v�c�ȓ_�ł��ˁB
�Ƃ���ŁC�t�F���}�[�_ - Wikipedia ���̋L�q
�@�E�t�F���}�[�_����3�ӂɉ��낵�������̑��͐��O�p�`���Ȃ��B
�͌��ł���ˁH
�����̗���F���炩�ɊԈႢ�ł��B��
�w���w�I���x�̉쐬�ɖv�����邱�ƂŁC��Ϗ[���������Ԃ��߂����Ă���܂��B
�V�N�C����ȍ~���X�������肢�v���܂��B
NO5�uamnesiac�v�@�@�@�@12/18�@�@�@15��08���@�@�@�@��M �X�V 1/4
���߂ĉ����܂����̂ŁA���傢�����܂��B
��ꂽ������
�����ɗ���F�lj����P��,���O�p�`�̈�ӂ̒����͂�����̓����ƈ���Ă��܂��B
NO6�ukasama�v
12/27
16��13���@�@ ��M �X�V 1/4
��ꂽ������
NO7�u��x�Ђ����v 12/30 09��11���@ ��M �X�V 1/4
��462�w�I�ȘA��������̉F
�m�ŒZ�����n
x+y+z=��(129) (��)
x^2+y^2+x*y=49 ---�@
y^2+z^2+y*z=64 ---�A
z^2+x^2+z*x=25 ---�B
�@-�A���Cx^2-z^2+y*(x-z)=-15.
����āC(x-z)*(x+y+z)=-15.
����āC1/(x+y+z)=(z-x)/15.
���l�ɂ��āC�A-�B���C1/(x+y+z)=(y-x)/39.
����āC(z-x)/15=(y-x)/39 ---�C
�����ŁCy=s*x, z=t*x
(s>0,t>0) �Ƃ����D
������C�ɑ�����āC(t-1)*x/15=(s-1)*x/39.
����āC t=(5*s+8)/13. ����āCz=t*x=(5*s+8)*x/13.
y=s*x���@�ɑ�����āC
x^2+(s*x)^2+x*(s*x)=49.
����āC1/x^2 =(1+s^2+s)/49
---�D
z=(5*s+8)*x/13���B�ɑ�����āC
((5*s+8)*x/13)^2+x^2+((5*s+8)/13)*x^2=25.
����āC1/x^2
=(((5*s+8)/13)^2+1+(5*s+8)/13)/25 ---�E
�D,�E���C
(1+s^2+s)/49=(((5*s+8)/13)^2+1+(5*s+8)/13)/25.
����2���������������āCs=64/25.
�D���Cx^2=49/(1+s^2+s)=625/129.
����āCx=25/��(129).
y=s*x=64/��(129).
z=(5*s+8)*x/13=40/��(129).
����āC
x+y+z=(1/��(129))*(25+64+40)=��(129).
[��@�Ɏg���Q�l�}] �ɂ�����₢�F
AP+BP+CP�̍ŏ��l��a,b,c,S�ŕ\���ƁC
sqrt((a^2+b^2+c^2)/2+2*sqrt(3)*S)�@(��)
�@
��ABC�̓����ɁC��AFB=��BFC=120���ƂȂ�悤�ȓ_F���Ƃ�D
(���̂悤�ȓ_F����������݂��邱�Ƃ́C��AVB=120������
�_V�̋O�Ղł���~�ʂƁC��BWC=120�������_W�̋O�Ղł���
�~�ʂ̌�_��F�ł��邱�Ƃ��画��D)
����ɁC��BDC�����O�p�`�ɂȂ�悤�ɁC��BC�Ɋւ��ē_A�Ƃ�
���Α��ɁC�_D���Ƃ�D
���̂Ƃ��C���̓�������ѕs���������藧�D
��ABC�̓����̔C�ӂ̓_P�ɑ��āC
AP+BP+CP��AD=AF+BF+CF�D
(�ؖ�)
��BFC+��BDC=120��+60��=180���ł��邩��C�l�p�`BFCD�͉~�ɓ��ڂ���D
����āC��BFD=��BCD=60���D
��AFD=��AFB+��BFD=120��+60��=180���ł��邩��C
3�_A,F,D�͓��꒼����ɂ���D
����āCAF+DF=AD ---�@
�l�p�`BFCD�Ƀg���~�[�̒藝��K�p���āC
DF*a=BF*a+CF*a.�@����āCDF=BF+CF ---�A
�@�C�A���CAD=AF+BF+CF.
�l�p�`PBDC�Ƀg���~�[�̕s������K�p���āC
BP*a+CP*a��DP*a. ����āCBP+CP��DP.
����āCAP+BP+CP=AP+(BP+CP)��AP+DP��AD.
�܂�CAP+BP+CP��AD�D (�ؖ��I)
AD���Ca,b,c,S�ŕ\���Ǝ��̂悤�ɂȂ�D
S=(1/2)*c*a*sin(��ABC)���Csin(��ABC)=2*S/(c*a).
��ABD�ɗ]���藝��K�p���āC
AD^2
=c^2+a^2-2*c*a*cos(��ABD)
=c^2+a^2-2*c*a*cos(��ABC+60��)
=c^2+a^2-2*c*a*(1/2)*(cos(��ABC)-(��3)*sin(��ABC))
=c^2+a^2-c*a*((c^2+a^2-b^2)/(2*c*a)-(��3)*2*S/(c*a))
=(1/2)*(a^2+b^2+c^2)+2*(��3)*S.
����āC
AD=sqrt((a^2+b^2+c^2)/2+2*sqrt(3)*S).
�lj����:
[���1]
�����`�̈�ӂ̒����́Csqrt(1/2),
���O�p�`�̈�ӂ̒����́Csqrt((5-sqrt(2)-sqrt(3*(1+2*sqrt(2))))/2).
(��)
���O�p�`�̈�ӂ̒����� s �Ƃ���ƁC
(sqrt(1-(s/2)^2)-(s/2)*sqrt(3))/sqrt(1/2)=1/sqrt(1-(s/2)^2)�D
����������āC
s=sqrt((5-sqrt(2)-sqrt(3*(1+2*sqrt(2))))/2)�D
[���2]
�����`�̈�ӂ̒����́Csqrt(2/5)�C
���O�p�`�̈�ӂ̒����́Csqrt(2/15)
(��)
�����`�̈�ӂ̒����� t �Ƃ���ƁC
(t/sqrt(2))^2+(t*sqrt(2))^2=1.
����āCt=sqrt(2/5).
���O�p�`�̈�ӂ̒����́C
t/sqrt(3)=sqrt(2/15).
(�ȏ�)
�����̗��ꁄ�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�X�V 12/7


�Q�l���@�F2023�N9��24��(���j����A�{���s�s�������z�[���ɂāA�H�R�m�搶�́u�����g���Ċy���ނȂ���������v�Ƃ����u�����Ă��܂����B���̒��ŁA�Ό����ɕ����Ă݂悤�ƌ����Ď���������܂����B
�u���_�����ԍŒZ�o�H�̖��v�ł��B �V���^�C�i�[���ƌ����Ă��܂��B�e�L�X�g��\���Ă����܂��B��ϋ����[���o�H��Ό����������Ă���܂��B
���̂Ƃ��̎ʐ^�ł��B

���O�p�`�̏ꍇ�@�@�@���l�p�`�̏ꍇ�@�@���܊p�`�̏ꍇ�@���Z�p�`�̏ꍇ
