�ߘa�S�N�Q���U��
 [���ꐯ]
[���ꐯ]
�@�@��409�����w�I�ȘA�������
�@�@�@�@����W���ԁF1��9���`2��6����
�@�@�@�@�@�@�@�@�m���J�����{�̎Z�z(3)�n
�ߘa4�N�p�Ж����܂��Ă��߂łƂ��������܂��B
��N�܂ł̂�����ɐ[�����Ӑ\���グ�܂��B����ɁA
���N���������������ڎ���܂��悤��낵�����肢�����܂��B

�@����_�s���J1����203�Ԓn�@�@���J�����_��
�@
�@�@�@�@�@
��̎ʐ^�́A�c�����N�i1865�N�j���F���i�V�ɍցj�̖�킪�������Z�������S���J�������{�{�O�n�����ɕ�[�����Z�z�ł����B
�ʐ^���u�a�Z�̊فv�ɂ�����̎Z�z�@�����{����̂��̂ł���B
�@
�O���407���ɑ����A�����408���ɑ����āA��U��A��V��ł��B
��U���
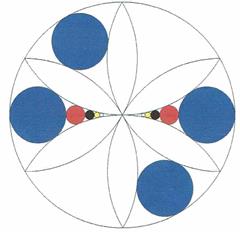 �@�O�~���ɂ��̉~�Ɠ������a�̉~�ʂ����E�㉺�ɍ��A���̌��ɐԍ�������5�̉~������B�O�~�a��m���Ċe�X�̗݉~�a�����߂�B
�@�O�~���ɂ��̉~�Ɠ������a�̉~�ʂ����E�㉺�ɍ��A���̌��ɐԍ�������5�̉~������B�O�~�a��m���Ċe�X�̗݉~�a�����߂�B
�o��ҁ@�c���@�@�P�䕺�q�`�M�@�@
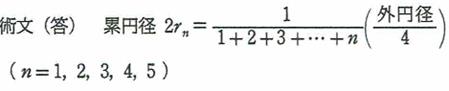
��7���
 �T�̐����`�A�ԁA���A�A���A���̂P�ӂ̍��͑��������B�Ԃ����Ƃ̖ʐς̘a����ѐƍ��Ɣ��̖ʐς̘a��m���Ĕ��̖ʐς����߂�B
�T�̐����`�A�ԁA���A�A���A���̂P�ӂ̍��͑��������B�Ԃ����Ƃ̖ʐς̘a����ѐƍ��Ɣ��̖ʐς̘a��m���Ĕ��̖ʐς����߂�B
�o��ҁ@����O�H���@�ؑ��Ћg�@�ލl
�����l�сF��蕶�̒��ŐԂ����Ƃ̖ʐς̘a�@�ƐԎ������25���遄

�⑫�@�@�W���[�J�[����p���̌W����������1�����Ԉ���Ă���Ǝw�E������܂����B�P�Uℓ�łȂ��P�Vℓ�ł��B
�Q�l�����@�@�@
�@�u���̎Z�z�̉���v�@���؏d���@��
�@��蕶�̒��̃J���[�摜�́u�W���[�J�[�v��
�lj����i�ҁ@�W���[�J�[����j

�u�W���[�J�[�v �@01/9 �@�@23��06�� ��M �X�V 2/6
��ꂽ���J�����{�̎Z�z�i�R�j�̑�U��A��V��A��������
�܂��A�lj�����������
�u��ӂ����̂炢��������v01/27 8��52�� ��M �X�V 2/6
��6���

���O�~�̔��a���q�A�E���炎�Ԗڂ̉~�̔��a����n�Ƃ��܂��B(����2)
�O�~�̒��S�n�A��̊O�~�̒��S�o�A���Ԗڂ̉~�̒��S�p�Ō��܂�O�p�`�ɎO�����̒藝��p���܂��B
![]()
![]()
![]()
��
![]()


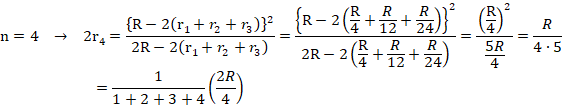
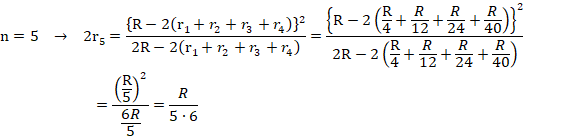
![]()
��7���
�����̐����`��1�ӂ̒��������A1�ӂ̒����̍������Ƃ��܂��B
����ƁA
![]()
![]()
![]() ��
��
![]() �ɓ���āA
�ɓ���āA
![]()
������Đ�������ƁA
![]()
![]() �ɂ��ĉ����ƁA
�ɂ��ĉ����ƁA
![]()
![]()
�������ŁA����
![]() �A
�A![]() �Ƃ��Ă݂�ƁA
�Ƃ��Ă݂�ƁA![]() �A
�A![]() �Ȃ̂ŁA
�Ȃ̂ŁA
![]()

����āA
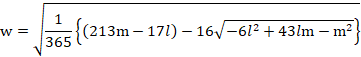
�lj����
(1)
�� ![]() �Ƃ���܂��B
�Ƃ���܂��B
�������A���̑傫���������̂悤�ł����A�傫���������ƍl����A![]() �ƂȂ�܂��B
�ƂȂ�܂��B
���̕����A�킩��₷���̂ŁA���̎��ōl���邱�Ƃɂ��܂��B
![]() �ƂȂ�܂��B
�ƂȂ�܂��B
�������̂Ƃ��A![]() �ƂȂ�܂��B
�ƂȂ�܂��B
�X�I��
![]() �Ƃ��܂��B
�Ƃ��܂��B
����̓I�ɂ������݂Ă݂܂��B
![]()
![]()
�E����
![]() �Ƃ��܂��B
�Ƃ��܂��B
![]()
![]()
![]()
![]()
�E![]()
![]() ������2�ł͂Ȃ��̂ŁA
������2�ł͂Ȃ��̂ŁA![]() �̉��ł��B
�̉��ł��B
![]()
![]()
![]()
![]()
�㔼��2�̕����������ʉ��������܂��B
��![]() �ł��B
�ł��B

![]()
![]()
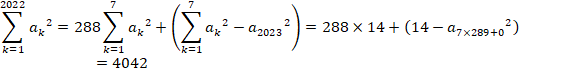
(2)
��(1)���A
![]() �Ȃ̂ŁA
�Ȃ̂ŁA![]()
![]()
![]()
![]()
![]()
��
![]()
![]()
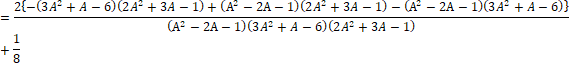
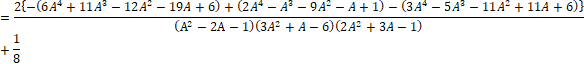
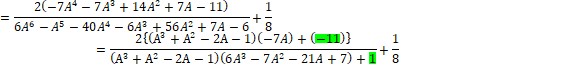
![]()
���ȏォ��A
![]()
�u�O�p��K�v�@�@�@�@02/04 11��50���@ ��M �X�V 2/6
��ꂽ��6��������B
��������7������ł��B
�����̗��ꂩ��̂��l�с@��7��̏p���Ƀ~�X������܂����B��
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
