令和６年９月１５日

[流れ星]

　　第445回数学的な連続応募解答

　　　＜解答募集期間：８月18日〜9月15日＞

［定積分（２）］

問題　

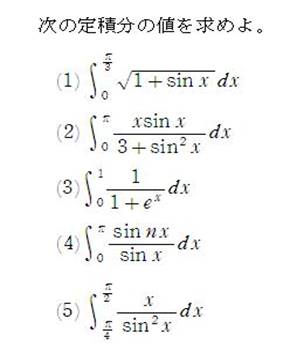
　追記　（４）のｎは正の整数（自然数）とする。

追加問題（出題者は「ジョーカー」）

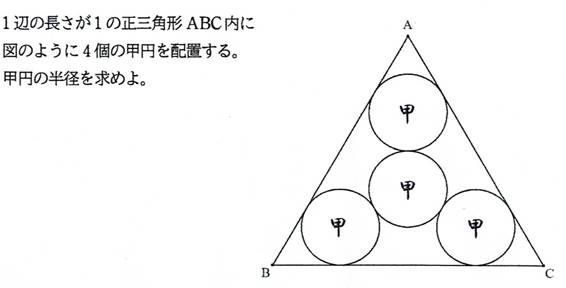
新シリーズ（正三角形の辺や円弧によって囲まれる図形内の４個の甲円の半径について）１,２,３問

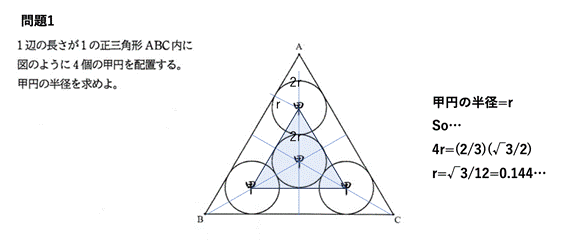
問題1

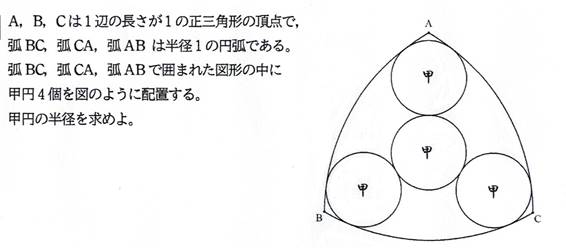
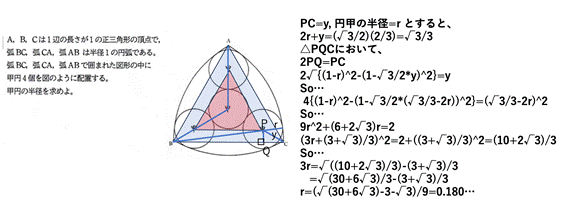
問題２

　

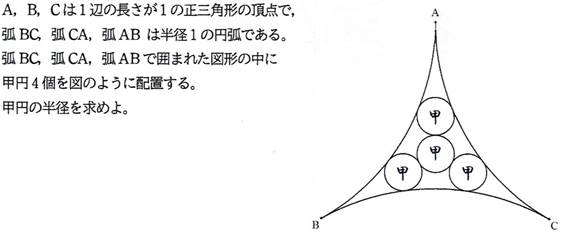
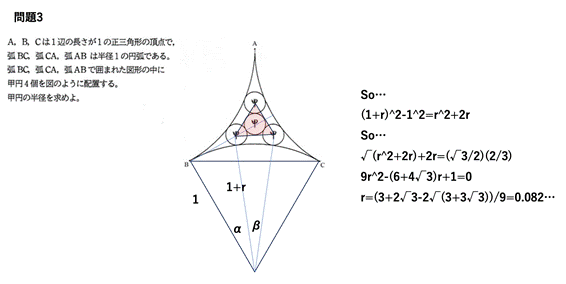
問題３

「ジョーカー」 　 8/18 　　 20時29分 受信 更新 9/15

寄せられた解答です

「スモークマン」 8/20 18時07分　 受信 更新 9/15

「スモークマン」 8/24 19時45分　 受信 更新 9/15

NO3「kasama」 8/28 00時59分　　 受信 更新 9/15

寄せられた解答です

＜水の流れ：問題（１）の積分区間の見間違いからの誤答＞

「kasama」 8/29 17時34分　　 受信 更新 9/15

問題（１）の訂正が送られた解答です

NO4「よふかしのつらいおじさん」 8/31 20時38分 受信 更新 9/15

寄せられた解答です

NO5「二度漬け白菜」 9/07 09時11分　 受信 更新 9/15

第445回数学的な応募問題 「定積分 (2)」の解答：

(1)(与式)=3-3^(1/2) (答)

(与式)

=∫_[x=0,π/3](1+sin(x))^(1/2)dx

=∫_[u=π/6,π/2](1+cos(u))^(1/2)du (x=π/2-uと置換)

=∫_[u=π/6,π/2](2*(cos(u/2))^2)^(1/2)du

=2^(1/2)*∫_[x=π/6,π/2]cos(u/2)du

=2*2^(1/2)*[sin(u/2)]_[π/6,π/2]

=3-3^(1/2).

(2)(与式)=(π/4)*log(3) (答)

(与式)=A とおく．

A=∫_[x=0,π](x*sin(x)/(3+(sin(x))^2))dx

=∫_[x=0,π](x*sin(x)/(4-(cos(x))^2))dx

=∫_[u=0,π]((π-u)*sin(u)/(4-(cos(u))^2))du (x=π-uと置換)

=π*∫_[u=0,π]sin(u)/(4-(cos(u))^2)du - ∫_[u=0,π]u*sin(u)/(4-(cos(u))^2)du

=π*∫_[u=0,π]sin(u)/(4-(cos(u))^2)du - A.

よって，

2*A=π*∫_[u=0,π]sin(u)/(4-(cos(u))^2)du

=π*(1/4)*∫_[u=0,π](sin(u)/(2-cos(u))+sin(u)/(2+cos(u)))du

=(π/4)*[log(2-cos(u))-log(2+cos(u))]_[0,π]

=(π/4)*2*log(3).

よって，A=(π/4)*log(3).

(3)(与式)=1+log(2)-log(1+exp(1)) (答)

(与式)=∫_[x=0,1]1/(1+exp(x))dx

=∫_[u=-1,0]1/(1+exp(-u))du (x=-uと置換)

=∫_[u=-1,0]exp(u)/(exp(u)+1)du

=[log(exp(u)+1)]_[-1,0]

=1+log(2)-log(1+exp(1)).

(4)

・nが偶数のとき：(与式)=0

・nが奇数のとき：(与式)=π (答)

まず，次の等式を証明する．

sin(x)≠0のとき，

Σ[k=0〜n-1]cos((2*k+1-n)*x)=sin(n*x)/sin(x).

(証明)

2*sin(x)*Σ[k=0〜n-1]cos((2*k+1-n)*x)

=Σ[k=0〜n-1]2*cos((2*k+1-n)*x)*sin(x)

=Σ[k=0〜n-1]2*sin(π/2+(2*k+1-n)*x)*sin(x)

=Σ[k=0〜n-1](cos(π/2+(2*k-n)*x)-cos(π/2+(2*k+2-n)*x))

=cos(π/2-n*x)-cos(π/2+n*x)

=2*sin(π/2)*sin(n*x)

=2*sin(n*x).

よって，Σ[k=0〜n-1]cos((2*k+1-n)*x)=sin(n*x)/sin(x). (証明終)

この等式を使えば，与式は次のように計算できる．

・nが偶数のとき：

(与式)=∫_[x=0,π](sin(n*x)/sin(x))dxｙ

=∫_[x=0,π](Σ[k=0〜n-1]cos((2*k+1-n)*x))dx

=[Σ[k=0〜n-1](1/(2*k+1-n))*sin((2*k+1-n)*x)]_[0,π]

=0.

・nが奇数のとき：

(与式)=∫_[x=0,π](sin(n*x)/sin(x))dx

=∫_[x=0,π](Σ[k=0〜n-1]cos((2*k+1-n)*x))dx

=[Σ[k=0〜n-1,k≠(n-1)/2](1/(2*k+1-n))*sin((2*k+1-n)*x)]_[0,π]

+[cos(0)*x]_[0,π]

=0+cos(0)*(π-0)

=π.

(5)(与式)=(π/4)+(1/2)*log(2) (答)

(与式)

=[log(sin(x))-x*cos(x)/sin(x)]_[π/4,π/2]=

=(π/4)+(1/2)*log(2).

[追加問題 1]

甲円の半径は，(1/12)*3^(1/2) (答)

甲円の半径をrとする．

xy直交座標を設定して考える．

A(0,0),

B((1/2)*3^(1/2),-1/2),

C((1/2)*3^(1/2),1/2)

となるように座標を設定する．

その中心が点Aに最も近い甲円をD，

甲円Dに接する甲円をEとする．

甲円Dの中心の座標は，D(2*r,0),

甲円Eの中心Eは，対称性により，三角形ABCの重心であるから，E((1/3)*3^(1/2),0).

DE=2*r であるから，AE=AD+DE=(2*r)+(2*r)=4*r.

よって，r=(1/4)*AE=(1/12)*3^(1/2).

[追加問題 2]

甲円の半径は，((2*3^(1/2)+10)/27)^(1/2)-(1/9)*(3)^(1/2)-1/3 (答)

甲円の半径をrとする．

xy直交座標を設定して考える．

A(0,0),

B((1/2)*3^(1/2),-1/2),

C((1/2)*3^(1/2),1/2)

となるように座標を設定する．

その中心が点Aに最も近い甲円をD，

甲円Dに接する甲円をEとする．

甲円Eの中心Eは，対称性により，三角形ABCの重心であるから，E((1/3)*3^(1/2),0).

甲円Dの中心の座標は，D((1/3)*3^(1/2)-2*r,0).

CD+r=1であるから，(CD)^2=(1-r)^2.

よって，((1/6)*3^(1/2)+2*r)^2+(1/2)^2=(1-r)^2.

これを解いて，r=((2*3^(1/2)+10)/27)^(1/2)-(1/9)*(3)^(1/2)-1/3.

[追加問題 3]

甲円の半径は，(-2/3)*((1/3)*(3^(1/2)+1))^(1/2)+(2/9)*3^(1/2)+1/3 (答)

甲円の半径をrとする．

xy直交座標を設定して考える．

A(0,0),

B((1/2)*3^(1/2),-1/2),

C((1/2)*3^(1/2),1/2)

となるように座標を設定する．

また，点(0,1)をFとする．

その中心が点Aに最も近い甲円をD，

甲円Dに接する甲円をEとする．

甲円Eの中心Eは，対称性により，三角形ABCの重心であるから，E((1/3)*3^(1/2),0).

甲円Dの中心Dの座標は，D((1/3)*3^(1/2)-2*r,0).

FD=1+rであるから，(FD)^2=(1+r)^2.

よって，((1/3)*3^(1/2)-2*r)^2+1^2=(1+r)^2.

これを解いて，r=(-2/3)*((1/3)*(3^(1/2)+1))^(1/2)+(2/9)*3^(1/2)+1/3.

(以上)

NO6「三角定規」 9/07 20時23分　 受信 更新 9/15

寄せられた解答です

今回，(2)の積分にやや手こずりましたが，Wolfram の助けも借り

試行錯誤していたら，なんとか出来ました。

＜水の流れ：前回同様グラフがあり求める面積が鮮明で分かりやすいです＞

「水の流れ」 　　　　　　　　　　　　　　 更新 9/15

皆さん、問題や質問に答えてください。一部でも構いませんから, 解答とペンネームを添えて, メールで送ってください。待っています。