令和７年１月５日

[流れ星]

　　第449回数学的な連続応募解答

　　　＜解答募集期間：12月8日〜1月５日＞

［ガウス記号(1)］

　

　問題

補足説明　実数xに対してxの整数部分を[x]で表す。

すなわち，[x]≦x<[x]+1　

[　]をガウス記号という。　　　　　　12月8日午後　記

追加問題（出題者は「ジョーカー」）　新作シリーズ5,6問目

問題1

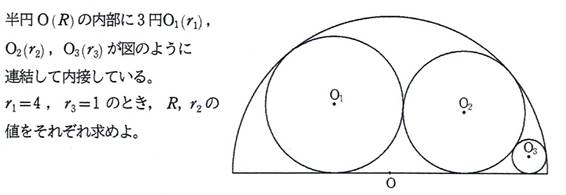
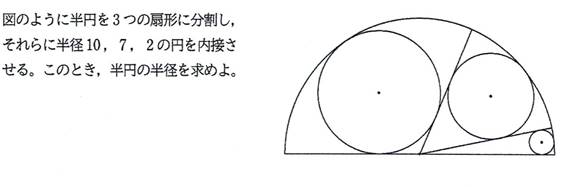
問題２

　

NO1「ジョーカー」 　 12/8 　 17時27分 受信 更新 1/5

寄せられた解答です

NO2「よふかしのつらいおじさん」 12/18 19時36分 受信 更新 1/5

寄せられた解答です

＜コメント：今回の問題ははじめよくわかりませんでしたが、定義式を使うとあったので、使ってみたら考えが進められることが解りました。

こんなのは初めてのことだったので面白かったです。

追加問題2は初めcosγの式で始めました。

すると、ｒの12次方程式になりました。（実質10次）

これは歯がたたないと思いましたが、問題図の実際の長さを物差しで測って、

比例式で解いてみると、22ぐらいの値になりました。

それで、ｒ-22で12次式を割ってみると、余りが0になり結構うれしかったです。

それで次数を下げるように考え、sinγの式にしました。この方が断然簡単でした。＞

N3「二度漬け白菜」 12//22 14時16分　 受信 更新 1/5

[問題1] x=-1/2,x=0,x=1,x=3/2 (答)

[x^2]+[x]-2*x=0 ---(A)

(A)を変形して，

x=([x^2]+[x])/2.

ここで，[x^2]+[x] は整数であるから，

(A)を満たすようなxは，

x=m もしくは x=m+1/2 (mは整数)

の形にかけるものに限る．

・x=m の場合：

x=mを(A)に代入して，

[m^2]+[m]-2*m=0.

m^2-m=0.

m=0 および m=1.

・x=m+1/2 の場合：

x=m+1/2を(A)に代入して，

[(m+1/2)^2]+[m+1/2]-2*(m+1/2)=0.

[m^2+m+(1/4)]+[m+1/2]-2*(m+1/2)=0.

(m^2+m)+(m)-2*m-1=0.

m^2-1=0.

m=-1 および m=1.

[問題 2] x=-1　および

0≦x<1なるすべての実数　および

-3^(1/2)<x≦-2^(1/2) なるすべての実数 (答)

[x^2]+[x]=0 ---(A)

x=m+α (mは整数，αは0≦α<1なる実数) とおいて，

(A)に代入して，

[m^2+2*m*α+α^2]+[m+α]=0.

⇒ m^2+[2*m*α+α^2]+m=0.

⇒ [2*m*α+α^2]=-m^2-m　---(B)

ここで，m≧1なるmは，(B)を満たさない．

また，m=0は(B)を満たす．

以下，m≦-1 の場合を考える．

m=-M (Mは正整数)とおける．

x^2-1<[x^2] および[x^2]=-[x]とから，

x^2-1<-[x].

この不等式に x=(-M+α) を代入して，

(-M+α)^2-1<M.

よって，M^2-2*M*α+α^2-1<M.

よって，M^2-2*M*α-M+α^2-1<0　---(C)

ここで，

(M^2-2*M*α-M+α^2-1)≧(M^2-2*M*1-M+α^2-1)≧(M^2-3*M-1)であるから，

(C)と合わせて，

M^2-3*M-1<0.　つまり，

M*(M-3)-1<0.

よって，M=1 or 2 or 3 である．

・M=1の場合：

m=-1を(B)に代入して，

[-2*α+α^2]=0.

0≦-2*α+α^2<1.

これを満たすαは，α=0 のみ．

・M=2の場合：

m=-2を(B)に代入して，

[-4*α+α^2]=-2.

-2≦-4*α+α^2<-1.

これを満たすαは，2-3^(1/2)<α≦2-2^(1/2)．

・M=3の場合：

m=-3を(B)に代入して，

[-6*α+α^2]=-6.

-6≦-6*α+α^2<-5.

これを満たすα(0≦α<1) は，存在しない．

[問題3] x=0, x=2^(1/2)，x=3^(1/2), x=2 (答)

x^2=[2*x] ---(A)

[2*x]≦2*x および (A) とから，

x^2≦2*x．よって，0≦x≦2 ---(B)

よって，[2*x]の値として考えられるのは，

[2*x]=0,1,2,3,4である．

[2*x]=0の場合：

(A)より，x=0. x=0は[2*x]=0も満たす．

[2*x]=1の場合：

(A),(B)より，x=1. x=1は[2*x]=1を満たさない．

[2*x]=2の場合：

(A),(B)より，x=2^(1/2). x=2^(1/2)は[2*x]=2も満たす．

[2*x]=3の場合：

(A),(B)より，x=3^(1/2). x=3^(1/2)は[2*x]=3も満たす．

[2*x]=4の場合：

(A),(B)より，x=2. x=2は[2*x]=4も満たす．

[問題 4 ] x=-3*3^(1/2),x=-5,x=3 (答)

x^2+2*[x]-15=0 ---(A)

(A)を変形して，

[x]=(15-x^2)/2.

これと，(x-1)<[x]≦x とから，

(x-1)<(15-x^2)/2≦x.

これを解くと，

-1-3*2^(1/2)<x≦-5 または 3≦x<-1+3*2^(1/2).

ここで，

-1-3*2^(1/2)=-5.242…

-1+3*2^(1/2)=3.242…

であるから，[x]の値としてあり得るのは，

[x]=-6,-5,3 である．

・[x]=-6の場合：

[x]=-6を(A)に代入して，

x^2=27.

よって，x=-3*3^(1/2),3*3^(1/2) となるが，

[x]=-6をみたすのは，x=-3*3^(1/2).

・[x]=-5の場合：

[x]=-5を(A)に代入して，

x^2=25.

よって，x=-5,5 となるが，

[x]=-5をみたすのは，x=-5.

・[x]=3の場合：

[x]=3を(A)に代入して，

x^2=9.

よって，x=-3,3 となるが，

[x]=3をみたすのは，x=3.

[問題 5] x=2 および x=46/7 および x=7 (答)

x*[x]+x-10*[x]+14=0 ---(A)

(A)を変形して，

(10-x)*[x]=14+x ---(B)

x≧10なるxは(B)を満たさない．

(x≧10なるとき，(10-x)*[x]≦0,14+x≧24.)

よって，x<10として考えればよい．

(B)より，[x]=(14+x)/(10-x)．

この等式と， x-1<[x]≦x とから，

x-1<(14+x)/(10-x)≦x．

これを解くと，

2≦x<4 または 6<x≦7.

よって，[x]の値として考えられるのは，

[x]=2,3,6,7である．

・[x]=2の場合：

(A)において[x]=2を代入して，x=2を得る．

x=2は，[x]=2を満たしている．

・[x]=3の場合：

(A)より，x=4を得るが，これは[x]=3を満たさない．

・[x]=6の場合：

(A)より，x=46/7を得る.これは[x]=6を満たす．

・[x]=7の場合：

(A)より，x=7を得る.これは[x]=7を満たす．

[追加問題1]

R=64/7, r_2=32/9 (答)

3円O_1,O_2,O_3が接している，点Oを通っている円Oの弦を L とする．

O_1,O_2,O_3 から L に下した垂線の足をそれぞれ H_1,H_2,H_3 とする．

(OH_1)^2=(OO_1)^2-(O_1H_1)^2=(R-r_1)^2-(r_1)^2=R*(R-2*r_1)より，

(OH_1)=(R*(R-2*r_1))^(1/2). 同様にして，

(OH_2)=(R*(R-2*r_2))^(1/2),

(OH_3)=(R*(R-2*r_3))^(1/2).

(H_1H_2)=(OH_1)+(OH_2) より，

2*(r_1*r_2)^(1/2)=(R*(R-2*r_1))^(1/2)+(R*(R-2*r_2))^(1/2).

この等式から，

R=2*(r_1)*(r_2)/((8*(r_1)*(r_2))^(1/2)-(r_1+r_2)) ---(A)

を得る．

また，(H_2H_3)=(OH_3)-(OH_2) より，

2*(r_2*r_3)^(1/2)=(R*(R-2*r_3))^(1/2)-(R*(R-2*r_2))^(1/2).

この等式から，

R=2*(r_2)*(r_3)/((8*(r_2)*(r_3))^(1/2)-(r_2+r_3)) ---(B)

を得る．

(A),(B)より，

2*(r_1)*(r_2)/((8*(r_1)*(r_2))^(1/2)-(r_1+r_2))=2*(r_2)*(r_3)/((8*(r_2)*(r_3))^(1/2)-(r_2+r_3)).

この等式から，

(r_2)=8*(r_1)*(r_3)/((r_1)^(1/2)+(r_3)^(1/2))^2

を得る．

これに (r_1)=4,(r_3)=1を代入して，

(r_2)=32/9.

(A)より，R=64/7.

[追加問題2]

求める半円の半径は，22 (答)

求める半円の半径をRとする．

半径 10, 7, 2 の円が内接している扇形の中心角の大きさを

それぞれ，2*α, 2*β, 2*γ とする．

sin(α)=10/(R-10), sin(β)=7/(R-7), sin(γ)=2/(R-2),

cos(α)=(R*(R-20))^(1/2)/(R-10),

cos(β)=(R*(R-14))^(1/2)/(R-7)

である．

(2*α)+(2*β)+(2*γ)=180°より，

(α+β)=(90°-γ).

よって，

cos(α+β)=cos(90°-γ)=sin(γ).

加法定理を使って，

cos(α)*cos(β)-sin(α)*sin(β)=sin(γ).

よって，

((R*(R-20))^(1/2)/(R-10))*((R*(R-14))^(1/2)/(R-7))-(10/(R-10))*(7/(R-7))=2/(R-2).

分母を払い，移項して，

(R-2)*((R*(R-20))^(1/2))*((R*(R-14))^(1/2))=70*(R-2)+2*(R-10)*(R-7).

両辺を2乗して整理すると，

R^2*(R-22)*(R*(R-8)^2+8)=0.

よって，R=22.

NO4「スモークマン」 12/22 22時05分　 受信 更新 1/5

(1)

[x^2]+[x]-2x=0

x=m, m+1/2

m^2+m-2m=m^2-m=m(m-1)=0…x=0,1

[(m+1/2)^2]+m-2m-1

=m^2-1=0…x=-1/2,3/2

結局

x=-1/2,0,1,3/2

(5)

x[x]+x-10[x]+14=0

x([x]+1)=10[x]-14

x=m+r/([x]+1)　0<=r<[x]+1=m+1

(m+r/(m+1))(m+1)=10m-14

m(m+1)+r=10m-14

m(m+1)+m-k=10m-14

m^2-8m+14-k=0

14-k=12,7…k=2,7

(m-2)(m-6)=0・・・x=2, 6+4/7

(m-1)(m-7)=0・・・x=7

結局…

x=2,46/7,7

NO5「kasama」 12/25 00時17分　　 受信 更新 1/5

寄せられた解答です

「kasama」 12/31 03時44分　　 受信 更新 1/5

問題（５）で他に答えがありましたから追加で寄せられた解答で

す。

「三角定規」 01/02 15時33分　 受信 更新 1/5

寄せられた解答です

＜コメメント：明けましておめでとうございます。

長年にわたり，考えて面白い＜難問＞の出題，有り難うございます。

今年も解答を送り続けようと思いますので，よろしくお願い致します。

さて，今回の＜問題449＞ですが，ガウス記号の問題(1)〜(5)は，ひたすら場合分けを行うものになってしまいました。エレガントではありませんが，分かりやすい解かな？ とは思います。

追加問題は，WolframAlpha の力を借りながら，やっと解を得ました。

例えば [問題１] で, O1の半径＝4, O3の半径＝1 と決めるために，出題者のジョーカーさんはもっと膨大な計算をやっておられるのですよね。[問題２] も同様です。いつもながら，脱帽です。＞

「水の流れ」 　　　　　　　　　　　　　　 更新 1/5

皆さん、問題や質問に答えてください。一部でも構いませんから, 解答とペンネームを添えて, メールで送ってください。待っています。