令和７年２月２日

[流れ星]

　　第450回数学的な連続応募解答

　　　＜解答募集期間：1月1日〜２月２日＞

［ガウス記号(２)］

　　令和７年乙巳（きのとみ）明けましておめでとうございます。

昨年までのご応募に深く感謝申し上げます。

今年も引き続きご愛顧賜りますようよろしくお願いいたします。

補足説明　実数xに対してxの整数部分を[x]で表す。

すなわち，[x]≦x<[x]+1　 [　]をガウス記号という。

　　　　　

追加問題１　（出題者は「ジョーカー」）　

＜水に流れ＞　小町算という和算を知っていますか？

小町算とは、１から９までの９個の数字を使う数のパズルです。

ルールは以下の３つだけです。

・１から９までの数字を全て使う

・１から９までの順番を変えてはいけない

・数と数との間に＋、−、×、÷、()、空白のいずれかを入れる

ちなみに、『空白』というのは、隣り合った数字をくっつけて一つの数字としてみてもOKという意味です。

例えば、１２３４…と並んでいた時、１＋２３＋４…のように23にしてもよいということです。ここで「ジョカー」さんからの出題です。

１から９の順に並んだ９つの数字の間に加減乗除の記号を入れて,その結果を2025にせよ。

（１）括弧を使わないとき

（２）括弧を1組使うとき

＜水の流れ：結果は幾つもありますので、解けた喜びを味わってください。＞

問題２　新作シリーズ7,8問目

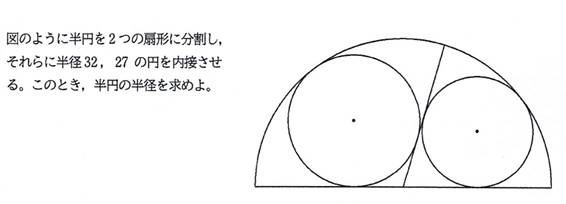
問題３

　

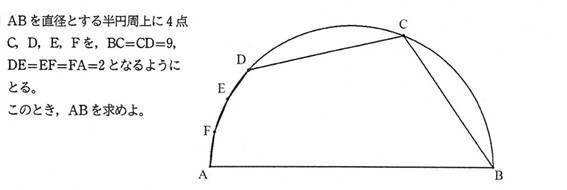
NO1「ジョーカー」 　 01/01 　 19時56分 受信 更新 2/2

寄せられた解答です

「ジョーカー」 　 01/04 　10時37分 受信 更新 2/2

寄せられた設問３の別解答です

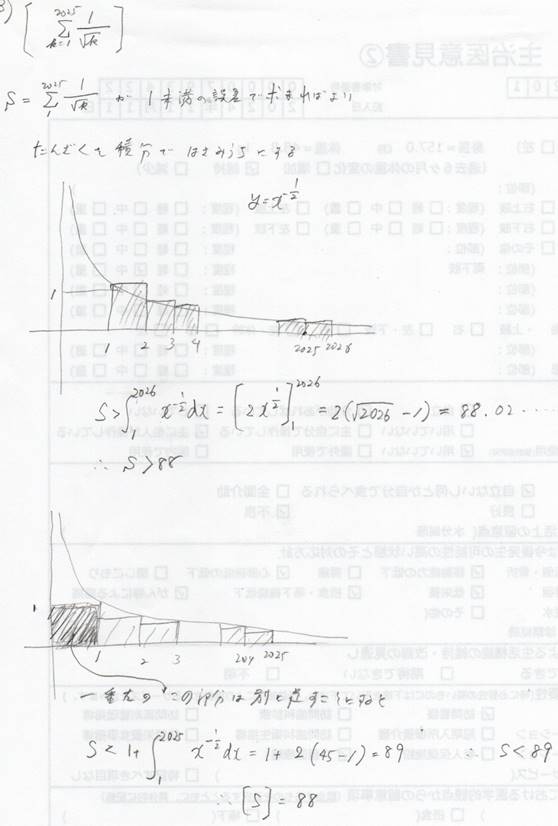
NO2「スモークマン」 01/05 18時34分　 受信 更新 2/2

で

NO３「よふかしのつらいおじさん」 10/10 17時26分 受信 更新 ２/２

寄せられた解答です

今回の問題は、追加の1番目は、いくつもあるとありましたが、

1つ見つけて終わりにしました。

かっこが2個のは2つ見つけました。

（5×5×9×9の発想で）

NO4「二度漬け白菜」 01//19 14時52分　 受信 更新 2/2

[設問 1]

-91/2≦x<-45 および　89/2≦x<45 (答)

[[x]^2+2*x]=2025 ---(A)

x=m+α (mは整数，αは0≦α<1なる実数) とおいて，

(A)に代入して，

[m^2+2*m+2*α]=2025

⇔ m^2+2*m+[2*α]=2025

⇔ [2*α]=2026-(m+1)^2　---(B)

ここで，[2*α]=0 or 1 であるから，場合分けして考える．

・[2*α]=0 の場合：

(B)より，0=2026-(m+1)^2 となるが，これを満たすようなmは存在しない．

・[2*α]=1 の場合：

(B)より，1=2026-(m+1)^2 となる. これを満たすようなmは m=-46,44.

また，[2*α]=1 ⇔ 1/2≦α<1.

[設問 2] n=2864 のみ (答)

(与式)

⇔[(n*(n+1)/2)^(1/2)]=2025

⇔2025≦(n*(n+1)/2)^(1/2)<2026

⇔2025^2≦(n*(n+1)/2)<2026^2

これを満たす正整数 n は，n=2864のみ．

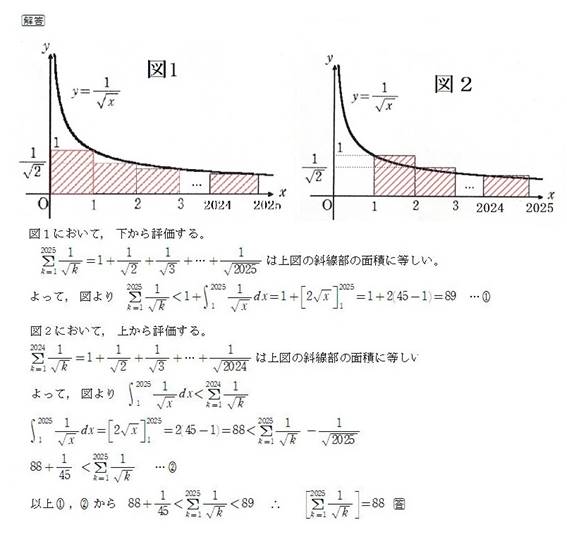
[設問 3] (与式)=88 (答)

2以上の任意の整数 n に対して，次の不等式が成り立つ．

2*(√(n)-1)+1/√(n) < Σ[k=1〜n](1/√(k)) < (2*(√(n)-1) + 1).

(証明)

kを任意の正の実数とする．

√(k+1) > √(k) が成り立っている．

よって，

√(k+1) >(√(k+1)+√(k))/2 > √(k).

よって，

1/√(k+1) < 2/(√(k+1)+√(k)) < 1/√(k).

すなわち，

1/√(k+1) < 2*(√(k+1)-√(k)) < 1/√(k).

よって，

Σ[k=1〜(n-1)](1/√(k+1)) < 2*Σ[k=1〜(n-1)](√(k+1)-√(k)) < Σ[k=1〜(n-1)](1/√(k)).

すなわち，

(Σ[k=1〜n]1/√(k) - 1) < 2*(√(n)-1) < (Σ[k=1〜n](1/√(k)) - 1/√(n)).

よって，

2*(√(n)-1)+1/√(n) < Σ[k=1〜n](1/√(k)) < (2*(√(n)-1) + 1).　(証明終)

この不等式に n=2025 を代入して，

88+1/45 < Σ[k=1〜2025](1/√(k)) < 89.

よって，

floor(Σ[k=1〜2025](1/√(k)))=88.

[設問 4] 求める個数は，3*44+1=133 個 (答)

kを正整数とする．

k^2≦n≦(k+1)^2-1 なる整数 n に対しては，

[√n]=k である．

k^2≦n≦(k+1)^2-1 を満たすような整数 n であって，

なおかつ，nがkの倍数となるものは，

n=k^2, n=k^2+k, n=k^2+2*k

の3つだけである．

求める個数は，(Σ[k=1〜44]3)+1=3*44+1=133.

---------------------------------------------

[追加問題 1]

(1) 1*2+345*6-7*8+9=2025.

(2) (1+2*3*4+5+6)*7*8+9=2025.　(1+234-5-6-7+8)*9=2025.

[追加問題 2]

求める半円の半径は，72 (答)

求める半円の半径をRとする．

半径 32, 27 の円が内接している扇形の中心角の大きさを

それぞれ，2*α, 2*β とする．

R>2*32=64 である．また，

sin(α)=32/(R-32), sin(β)=27/(R-27) である．

2*α+2*β=180°であるから，

α=90°-β. よって，

cos(α)=cos(90°-β)=sin(β).　よって，

(R*(R-64))^(1/2)/(R-32)=27/(R-27).

両辺を2乗して，分母を払って整理すると，

(R-72)*((R-46)*R^2+144*R+10368)=0.

R>64であるから，((R-46)*R^2+144*R+10368)>0.

よって，(R-72)=0.

[追加問題 3]

AB=16 (答)

線分ABの中点を O とする．

また，OA=r，∠BOC=2*α，∠AOF=2*β とおく．

AB>AF より，2*r>2. よって，r>1.

sin(α)=9/(2*r)，sin(β)=1/r である．

4*α+6*β=180°であるから，

3*β=90°-2*α.

よって，

sin(3*β)=sin(90°-2*α)=cos(2*α).

よって，

3*sin(β)-4*(sin(β))^3=1-2*(sin(α))^2.

よって，

3*(1/r)-4*(1/r)^3=1-2*(9/(2*r))^2.

両辺に r^3 を掛けて整理すると，

(r-8)*(2*r^2+10*r-1)=0.

r>1であるから，(2*r^2+10*r-1)>0.

よって，(r-8)=0.

AB=2*r=16.

-------------------------------------

[設問1]の問題を，当初，

「 [[x^2]+2*x]=2025 となる実数xの範囲を求めよ．」

という問題だと勘違いして考えていました．

これはこれで面白い問題だと思います．

[追加問題3]の結果から，等式

4*Arcsin(9/16)+6*Arcsin(1/8)=π

が成立することがわかりますね．

N5「kasama」 01/20 　　　00時43分　　 受信 更新 2/2

寄せられた解答です

N6「三角定規」 01/31 　　　21時46分　　 受信 更新 2/2

寄せられた解答です

今回の [設問４] は論証が雑で，も少し丁寧な議論が必要か，とも思います。

「水の流れ」 　　　　　　　　　　　　　　 更新 2/2

皆さん、問題や質問に答えてください。一部でも構いませんから, 解答とペンネームを添えて, メールで送ってください。待っています。