令和７年５月２５日

[流れ星]

　　第454回数学的な連続応募解答

　　　＜解答募集期間：4月27日〜5月25日＞

［素数の問題］

問題１　を素数,を整数とするとき,次の等式を満たす組をすべて求めよ。

（１）

２）

（３）　

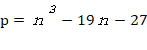
出典　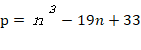　　（2021年　明治大学）

問題２　を素数とするとき,次の等式を満たす組をすべて求めよ。

（１）　　　　（2021年　お茶の水大学）

　（２）　　

出典　　　　（2021年　奈良女子大学）

問題３　△ABCにおいて,三辺の長さをそれぞれ,ＢＣ＝ａ,ＣＡ＝ｂ,ＡＢ＝ｃ

とおく。

　　等式　を満たすとき, △ABCはどんな三角形か。

　　ただし、 は素数, は整数とする。

参考文献　BLUEBACKS　大学受験で語る数論の世界　清水健一　講談社

追加問題（出題者は「ジョーカー」）　新作シリーズ

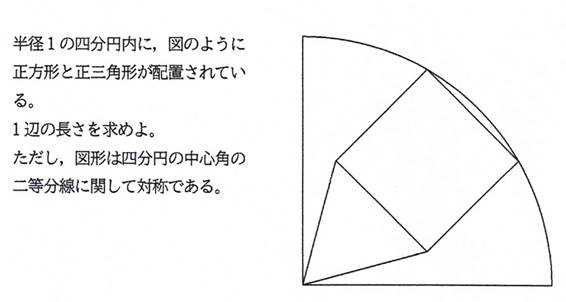
四分円内の正方形と正三角形の1辺について『１』　

問題１　　シリーズ3問目

正方形と正三角形の1辺が等しいとき(辺を共有する),

問題２　シリーズ4問目

正方形と正三角形の1辺が等しいとき(辺を共有する),

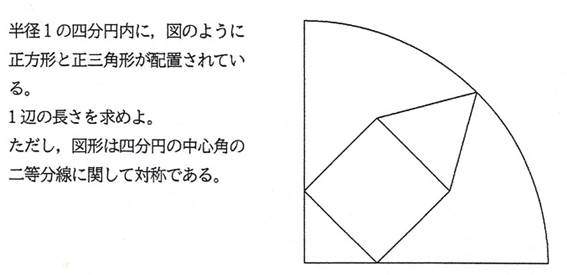
NO1「ジョーカー」 　 04/27　 14時49分 受信 更新 5/25

寄せられた解答です

NO1「スモークマン」 　 04/28　 12時33分 受信 更新 5/25

問題１

(1)

(n-18)^2=n^2-36n+324

So…

p=(n-18)^2-1

=(n-19)(n-17)

So…

n-19=1…n=20…p=3

n-19=-1…n=18…なし

n-17=1…n=18…なし

n-17=-1…n=16…p=3

結局、n=16,20 のとき、p=3

(2)

p=(n+2)(n^2-2n+4)

So…n+2 or n^2-2n+4=±1

・n+2=1…n=-1…p=7

・n+2=-1…n=-3・・・少なくともn>-2なのでなし

・n^2-2n+4=1…(n-1)^2=-3+1=-2<0 でなし

・n^1-2n+4=-1…同じくなし

結局、n=-1 のとき、p=7

(3)

・n=3m のとき

27m^3-57m-27

=3(9m^3-19m-9)

9m^3-19m-9=1

(m+1)(3m-5)(3m+2)=0

So…n=-3 のとき、p=3

・n=3m-1 のとき

(3m-1)^3-19(3m-1)-27=27m^3-27m^2-48m-9

9m^3-9m^2-16m-3=1

(m-2)(3m+1)(3m+2)=0

So…n=5 のときp=3

・n=3m+1 のとき

(3m+1)^3-19(3m+1)-27=27m^3+27m^2-48m-45

9m^3+9m^2-16m-15=1

(m+1)(3m-4)(3m+4)=0

So…n=-2 のとき p=3

結局、n=-3,-2,5 のとき、p=3

問題２

(1)

qは奇素数とわかる。

q=3のとき、3^2+2=11

q=6m±1…(6m±1)^2+2は3の倍数なのでなし

結局、(p,q)=(11,3)

(2)

q=2のとき、p^2=12*2+1=25…p=5

q=3のとき、p^2=37…なし

(p-1)(p+1)=12q

p=6m±1 のとき、

6m*(6m±2)=12m(m±1)=12q…qはm=1 or 2のとき3 or 2のみ

以上から、(p,q)=(5,2)

問題３

余弦定理から

a^2+(a+m)^2-2*a(a+m)*cos60°

=a^2+(a+m)^2-a(a+m)

=a^2+am+m^2<(a+m)^2

So…

((a+m)-k)^2=a^2+am+m^2

-2k(a+m)+am+k^2=0

a(m-2k)-2k(m-2k)=3k^2

(a-2k)(m-2k)=3k^2

a-2k=1,3,k,k^2,3k,3k^2

a=2k+1,2k+3,3k,k^2+2k,5k,3k^2+2k

m=上の逆順

a,b=a+mはともに素数

(a,b)=(2k+1,3k^2+4k+1),(2k+3,k^2+4k+3)

b=3k^2+4k+1=(3k+1)(k+1)・・・k=0 or -2

b=k^2+4k+3=(k+1)(k+3)・・・k=0 or -2

k=0 以外は、aが負の数となるので無理。

結局、各辺が素数の正三角形だけですね ^^

ジョーカー様の追加問題

(1)

2x^2(1-cos150°)

=2x^2(1+√3/2)=1

So…

x=√(2-√3)=0.5176…

(2)

(√3/2+1+1/2)x=1

So…

x=1-√3/3=0.4226…

以上です。

問題３はいわゆる「ナゴヤ」とか「ハナミ」と言われる三角かと思うも、a,bが素数にはならないので...

上のような考察になりました ^^

NO3「よふかしのつらいおじさん」 04/29 21時35分 受信 更新 5/25

「よふかしのつらいおじさん」 05/08 16時31分 受信 更新 5/25

寄せられた解答です

NO4「kasama」 05/10 ００時２２分　　 受信 更新 5/25

寄せられた解答です

NO5「三角定規」 05/10 ２１時１４分　　 受信 更新 5/25

寄せられた解答です

N06「浜田明巳」　　　　05/15 18時34分　 受信 更新 5/25

寄せられた解答です

NO7「二度漬け白菜」 05/20 　　　　19時42分　 受信 更新 5/25

[問題1]

(1)p=n^2-36*n+323を満たす(p,n)は，(p,n)=(3,16),(3,20) (答)

p=n^2-36*n+323=(n-19)*(n-17) であること，および

(n-19)<(n-17) であることから，

(n-19,n-17)=(-p,-1) or (n-19,n-17)=(1,p).

前者の場合は，n=16,p=3.

後者の場合は，n=20,p=3.

(2)p=n^3+8を満たす(p,q)は，(p,n)=(7,-1)のみ．(答)

n^3+8=(n+2)*((n-1)^2+3) となることに注意する．

n≦-2 のときは，(n+2)≦0であるから，n^3+8≦0．

n=-1 のときは，n^3+8=7. これは素数．

n≧0 のときは，(n+2)≧2, ((n-1)^2+3)≧3 であることから，

n^3+8は必ず合成数になる．

(3)p=n^3-19*n-27を満たす(p,n)は，(p,n)=(3,-3),(3,-2),(3,5) (答)

n^3-19*n-27は常に3の倍数である．

(なぜなら，n≡0(mod 3)ならば，n^3-19*n-27≡0^3-19*0≡0(mod 3).

n≡1(mod 3)ならば，n^3-19*n-27≡1^3-19*1≡-18≡0(mod 3).

n≡2(mod 3)ならば，n^3-19*n-27≡2^3-19*2≡-30≡0(mod 3). )

よって，p=n^3-19*n-27となるような素数pは，p=3に限る．

3=n^3-19*n-27.　(n-5)*(n+2)*(n+3)=0.

[問題2]

(1) p=q^2+2 を満たす(p,q)は，(p,q)=(11,3) のみ (答)

qを3で割った余りで場合分けして考える．

・q≡0 (mod 3)の場合：

qが素数であることから，q=3.

このとき，q^2+2=3^2+2=11. 11は素数．

・q≡1 (mod 3)の場合：

q^2+2≡1^2+2≡3≡0 (mod 3)．

よってp=q^2+2となるような素数pは，p=3に限る．

このとき，q^2=p-2=3-2=1となるが，これを満たす

素数qは存在しない．

・q≡2 (mod 3)の場合：

q^2+2≡2^2+2≡6≡0 (mod 3)．

よってp=q^2+2となるような素数pは，p=3に限る．

このとき，q^2=p-2=3-2=1となるが，これを満たす

素数qは存在しない．　

(2)p^2=12*q+1を満たす(p,q)は，(p,q)=(5,2) のみ (答)

p^2=12*q+1≧12*2+1=25より，p≧5.

よって，p=6*k-1 or p=6*k+1 (kは1以上の整数)とかける．

・p=6*k-1の場合：

(6*k-1)^2=12*q+1より，k*(3*k-1)=q.

よって，k=1 かつ 3*k-1=q となる．

よって，p=5,q=2.

・p=6*k+1の場合：

(6*k+1)^2=12*q+1より，k*(3*k+1)=q.

よって，k=1 かつ 3*k+1=q となる．

よって，p=7,q=4となるが，q=4は素数ではない．

[問題3]

ΔABCは正三角形 (答)

対称性より，a≧b として考えればよい．

・a=bの場合：：

c^2=a^2+b^2-a*b と a=b とから，c^2=a^2.

よって，c=a=b となる．

・a>bの場合：

c^2=a^2+b^2-a*b を変形して，(c+b-a)*(c+a-b)=a*b ---(★)

ここで，a,b,c はいずれも正整数 かつ 三角形の三辺の長さであること，

および a>b とから，2つの整数 (c+b-a)，(c+a-b)は，

1≦(c+b-a)<(c+a-b) を満たす．

またa,bは素数でもあるから，(★)より，

(c+b-a, c+a-b)=(1,a*b) or (c+b-a, c+a-b)=(b,a)

の2つの場合が考えられる．

前者の場合は，c+b-a=1 かつ c+a-b=a*b の2式から，

2*b-2*a=1-a*b. よって，(2-b)*(a+2)=3 となるが，

この等式を満たす素数a,bは存在しない．

後者の場合は，c+b-a=b かつ c+a-b=a の2式から，

c=a=bとなるが，これはa>bに反する．

[追加問題1]

一辺の長さは， (1/2)*(6^(1/2)-2^(1/2))(答)

正方形の一辺の長さを s とおくと，

((s/2)*3^(1/2)+s)^2+(s/2)^2=1^2.

これを解いて，s=(1/2)*(6^(1/2)-2^(1/2)).

[追加問題2]

一辺の長さは，1-3^(-1/2) (答)

正方形の一辺の長さを s とおくと，

(s/2)+s+(s/2)*3^(1/2)=1.

これを解いて，s=1-3^(-1/2).

「水の流れ」　　　　　　　　　　　　　　　　　　　更新 5/25

問題１の解答

　　　　　　　　　　　　　　　　　　　

問題２の解答

問題３の解答