令和７年６月２２日

[流れ星]

　　第455回数学的な連続応募解答

　　　＜解答募集期間：5月25日〜6月22日＞

［最大値・最小値］

　

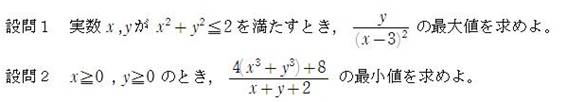
　設問１は2013年東邦大学（医学部）入試問題の類題

　設問２は2006年一橋大学入試問題の類題

追加問題（出題者は「ジョーカー」）　新作シリーズ

四分円内の正方形と正三角形の1辺について『１』　

問題１　　シリーズ5問目

正方形と正三角形の1辺が等しいとき(辺を共有する),

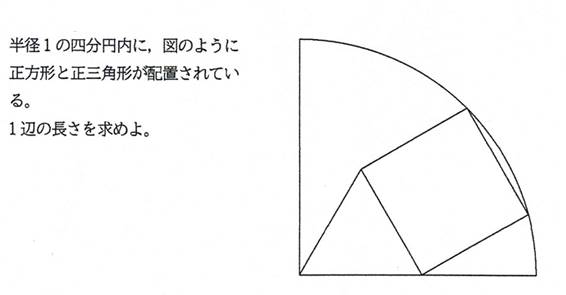
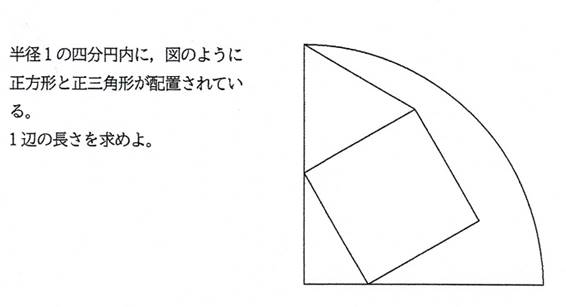
問題２　シリーズ6問目

正方形と正三角形の1辺が等しいとき(辺を共有する),

NO1「ジョーカー」 　 05/25 　　 18時46分 受信 更新 6/22

「ジョーカー」 　 05/26　　 23時06分 　　 受信 更新 6/22

類題を含めた解答です

NO2「浜田明巳」　　　　05/28 00時10分　 受信 更新 6/22

寄せられた設問１,２の解答です

寄せられた追加問題１,２の解答です

NO3「よふかしのつらいおじさん」 05/31 11時33分 受信 更新 6/22

寄せられた解答です

NO4「三角定規」 06/03 20時38分　 受信 更新 6/22

寄せられた解答です

NO5「kasama」 06/08 00時58分　　 受信 更新 6/22

寄せられた解答です

NO6「スモークマン」 06/08 11+時15分　 受信 更新 6/22

(1)

x^2+y^2<=2 の円

y/(x-3)^2=k

y=k(x-3)^2 は放物線

kの最大値はこの放物線とx^2+y^2=2 が接するとき

y=k(x-3)^2

t^2+(k(t-3)^2)^2=2

so…

k^2=(2-t^2)/(t-3)^4

((2-t^2)/(t-3)^4)’=2(t^2+3t-4)/(t-3)^5

t^2+3t-4

=(t-1)(t+4)=0

So…-4<t<1で傾き正、1<t<3で傾き負、3<tで正

So…t=1 のとき、k^2=1/2^4

k=1/4 のときが最大

(2) はカンニング Orz

4x^2+1/(2x)+(1/(2x)>=3

4x^3+1>=3x

So…

与式={4(x^3+1)+4(y^3+1)+6}/(x+y+2)

>=(3x+3y+6)/(x+y+2)=3

So,,,最小値は3

4x^2=1/(2x)…x=1/2 のとき

これは思いつけないんじゃ？ ^^;

「スモークマン」 06/08 21時54分　 受信 更新 6/22

追加問題１

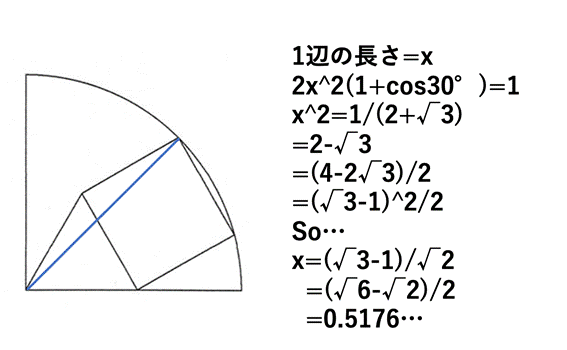
追加問題２

NO7「二度漬け白菜」 06/15 14時42分　 受信 更新 6/22

第455回の応募問題の解答：

[問題 1]

求める最大値は，(1/4)　(答)

x^2+y^2≦2より，

-2^(1/2)≦x≦2^(1/2)，

-(2-x^2)^(1/2)≦y≦(2-x^2)^(1/2)

である．

x=k (ただし，-2^(1/2)≦k≦2^(1/2)) とおいて，kを固定して考える．

y/(x-3)^2=y/(k-3)^2は，y=(2-k^2)^(1/2)のときに

最大値 (2-k^2)^(1/2)/(k-3)^2 をとる．

ここで，

f(k)=(2-k^2)^(1/2)/(k-3)^2 ( -2^(1/2)≦k≦2^(1/2))

とおく．

f(k)の最大値が求めるものである．

f(-2^(1/2))=f(2^(1/2))=0 である．

また，-2^(1/2)<k<2^(1/2) のときには，

(d/dk)f(k)=(1/(k-3)^4)*(3-k)*(k+4)*(1-k)*(2-k^2)^(-1/2)

であるので，f(k)は，k=1のときに最大値 f(1)=(2-1^2)^(1/2)/(1-3)^2=(1/4)

をとることがわかる．

以上よりf(k)の最大値は，max(0,1/4)=1/4.

[問題 2]

求める最小値は，3　(答)

x+y+2=kとおく．

x≧0,y≧0 より，k≧2.

y=-x+(k-2)≧0とから，0≦x≦(k-2).

y=-x+(k-2)を与式に代入する．

(与式)

=(4*(x^3+y^3)+8)/(x+y+2)

=4*(x^3+(-x+(k-2))^3+2)/(k)

=(4/k)*(3*(k-2)*x^2-3*(k-2)^2*x+(k-2)^3+2)

=12*(1-2/k)*(x-(k-2)/2)^2+(k-3)^2+3

(=g(x)とおく)

k=2のとき，g(x)=4.

k>2のときには，g(x)は下に凸の放物線であって，

x=(k-2)/2のときに最小値 (k-3)^2+3 をとる．

さらに，(k-3)^2+3は k=3 のとき，最小値 3 をとる．

以上より，(与式)の最小値は 3． (x=y=1/2のときに実現する)

(別解)

xを実数とするとき，(x-1/2)^2≧0.　よって，(x^2-x+1)≧(3/4)．

よって，(x+1)≧0なるとき，

(x^2-x+1)*(x+1)≧(3/4)*(x+1),

つまり，(x^3+1)≧(3/4)*(x+1) が成り立つ．(等号はx=1/2のとき成立)

(与式)

=(4*(x^3+y^3)+8)/(x+y+2)

=(4*(x^3+1)+4*(y^3+1))/(x+y+2)

≧(4*(3/4)*(x+1)+4*(3/4)*(y+1))/(x+y+2)　(等号はx=y=1/2のとき成立)

=(3*x+3*y+6)/(x+y+2)

=3.

[追加問題1]

一辺の長さは，(1/2)*(6^(1/2)-2^(1/2))(答) (答)

正方形の一辺の長さを s とおくと，

((s/2)*3^(1/2)+s)^2+(s/2)^2=1^2.

これを解いて，

s=(1/2)*(6^(1/2)-2^(1/2)).

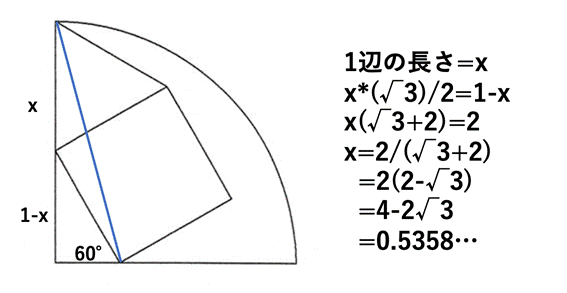
[追加問題2]

一辺の長さは， 4-2*3^(1/2) (答)

正方形の一辺の長さを s とおくと，

s+(s/2)*3^(1/2)=1.

これを解いて，

s=4-2*3^(1/2).

「水の流れ」　　　　　　　　　　　　　　　　更新 6/22

設問１の解答

設問２の答