�ߘa�V�N11��11��
 [���ꐯ]
[���ꐯ]
�@�@��460�����w�I�ȘA�������
�@�@�@����W���ԁF10��12���`11��11����
�m�O�p�`�̖ʐς̓�
�{NHK�̎Z�z�n
�@
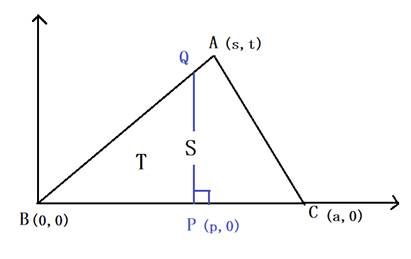
�@�O�p�`�`�a�b�ɂ�����,�`�a���`�b�Ƃ���B�ӂa�b��̓_�o��萂��������,
�ӂ`�a�̌�_���p�Ƃ���B���̂Ƃ�,�����o�p�͎O�p�`�`�a�b�̖ʐς�����Ă���B������,�O�ӂ̒������a�b����,�b�`�����C�`�a�����Ƃ���B
�ݖ�P�@�ӂa�o�̒��������C���C���ŕ\���B
�ݖ�Q�@�_�o����}����B
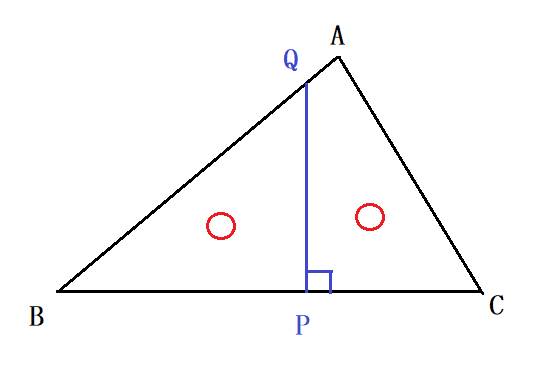
���肢�F�ݖ�Q���_�o�̍�}���@��������܂���B�����Ă��������B
�ʖ��@��9��2��(��)NHK����TV�ߌ�11������́u�Ő[���{�����@�a�Z�@�Z�z�v�ŕ�����聄�@
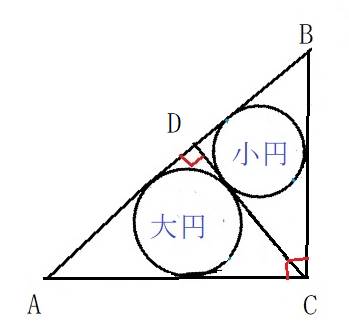
��C=90���̒��p�O�p�`�`�a�b�ɂ�����,�_�b����Εӂ`�a�ɐ}�̂悤�ɐ����b�c�������B���`�b�c�A���a�b�c�̓��ډ~���~�A���~�Ƃ���B��~,���~�̒��a�����ꂼ��A�R�Q��,�Q�S�ڂƂ����Ƃ�, ���p�O�p�`�`�a�b�̂R�ӂ̒��������߂�B
�lj�����i�o��҂́u�W���[�J�[�v�j�@�V��V���[�Y
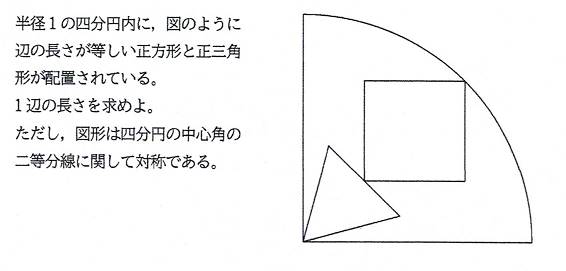
�l���~���̐����`�Ɛ��O�p�`��1�ӂɂ��āw�Q�x�@
���P�@�@�V���[�Y7���
�����`�Ɛ��O�p�`��1�ӂ��������Ƃ�(�ӂ����L���Ȃ�),
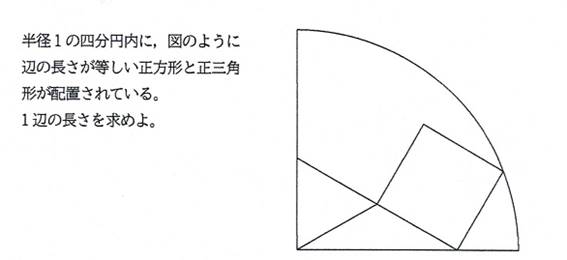
���Q�@�V���[�Y8���
�����`�Ɛ��O�p�`��1�ӂ��������Ƃ�(�ӂ����L���Ȃ�),
NO1�u�W���[�J�[�v �@ 10/12�@�@09��56�� ��M �@�@�@�X�V 11/11
��ꂽ������
NO2�u��ӂ����̂炢��������v 10/14 22��30�� ��M �X�V 11/11
�@��ꂽ������
NO3�ur-de-r�v�@�@
10/17�@ 00��31�� ��M �X�V 11/11
�@��ꂽ������
�@��ꂽ�ʖ���������
NO4�ukasama�v 10/29 17��31���@�@ ��M �X�V 11/11
��ꂽ������
NO5�u�O�p��K�v 10/29 17��45���@ ��M
�X�V 11/11
��ꂽ������
���R�����g�F����̖��, �ȑO�ǂ����Ō����悤�ȒW���L��������̂ł����C
������ƍl�����͍̂����߂Ăł��B
�����Ă݂�ƁC�ʔ������ʂ��o�ė�����̂ł��ˁB
[�ݖ�2]�̍�}�́C[1]�̌��ʂ̌`����C�O�����̒藝�����܂��g����悤�ɍl���܂����B��
NO6�u��x�Ђ����v 11/08 10��29���@��M �X�V 11/11
[�ݖ�1]
BP=(1/2)*��(a^2+c^2-b^2) (��)
���_A�������BC�։��낵�������̑���H�Ƃ���D
AH=x, BH=y �Ƃ����D
�܂��C��ABC�̖ʐς�S�Ƃ����D
�O�����̒藝���C
x^2+y^2=c^2, x^2+(a-y)^2=b^2.
����2������Cy=(a^2+c^2-b^2)/(2*a) ---(�@)
S=(1/2)*a*x ���C(S/x)=(a/2) ---(�A)
��ABH �� ��QBP �ł��邩��C
(y^2):(BP)^2 = (x*y/2):(S/2).
����āC
(BP)^2
=(y^2)*(S/2)/(x*y/2)
=(S/x)*y
=(a/2)*y (��A) ---(��)
=(a^2+c^2-b^2)/4 (��@)
����āC
BP=(1/2)*��(a^2+c^2-b^2).
[�ݖ�2]
�_P�͎��̂悤�Ȏ菇�ō�}�ł���D
���_C�𒆐S�Ƃ��锼�a y/8 �̉~��
K_1 �Ƃ���D
K_1�ƒ���BC��2�̌�_�̂����C����BC��ɂ���
���̂� D, ����BC��ɂȂ����̂� E �Ƃ���D
E�𒆐S�Ƃ��锼�a BD �̉~�� K_2 �Ƃ���D
����BE�̒��_�� M �Ƃ��CM�𒆐S�Ƃ��锼�a BM
�̉~�� K_3 �Ƃ���D
2�̉~ K_2, K_3 �̌�_(�̂�����1��)�� T �Ƃ���D
���_B�𒆐S�Ƃ��锼�a BT �̉~�� K_4
�Ƃ����Ƃ��C
K_4�Ɛ���BC�Ƃ̌�_�����߂�_ P �ł���D
(��L�̎菇�œ_P����}�ł��邱�Ƃ̐���)
����(y/8)�́C����BH�̒�����1/8�ł��邩��C�����
�R���p�X���g���č̐��\�D
�܂��C��BTE�́C��BTE=90���̒��p�O�p�`�ł���D
(���TBM=���Ƃ����ƁCBM=TM���C��BTM=��. ����āC��TME=2*���D
TM=EM���C��ETM=(1/2)*(180��-��TME)=90��-��.
����āC��BTE=��BTM+��ETM=��+(90��-��)=90���D)
����āC�O�����̒藝���C
(BT)^2=(BE)^2-(ET)^2=(a+y/8)^2-(a-y/8)^2=(a/2)*y�D
(��)���C(BP)^2=(a/2)*y�ł��邩��C
(BT)^2=(BP)^2. ����āCBT=BP.
NHK�̎Z�z�̖��F
AB=100�ځCBC=60�ځCCA=80�ځ@(��)
��~�̔��a�� x �C ���~�̔��a�� y �Ƃ��C(x/y)=t
�Ƃ����D
�܂��CAB=c,BC=a,CA=b �Ƃ����D
��CAB �� ��DCB �� ��DAC �ł���D
��DCB �� ��DAC ���C(y/a)=(x/b).
����āC
b=(x/y)*a=t*a ---(1)
c=��(a^2+b^2)=��(a^2+(t*a)^2)=a*��(1+t^2)
---(2)
��CAB�̓��ډ~�̔��a�� r �Ƃ���D
��CAB�̖ʐς�2�ʂ�̕��@�ŕ\�����Ƃɂ��C
(1/2)*a*b=(r/2)*(a+b+c) ---(3)
��CAB �� ��DAC �ł��邱�Ƃ��C(r/c) = (y/a).
����āCr=(c/a)*y ---(4)
(1),(2),(4)��(3)�ɑ�����āC
a*(t*a)=(��(1+t^2))*(y)*(a+(t*a)+a*��(1+t^2))
��D����āC
a=(1/t)*(��(1+t^2))*(y)*(1+t+��(1+t^2)).
y=12,t=(16/12)=(4/3)�������āCa=60.
���̂Ƃ��C
b=t*a=80,c=a*(1+t^2)^(1/2)=100.
[�lj���� 1]
��ӂ̒����́C(2/5)*(2*��2 - ��3) (��)
��ӂ̒�����r�Ƃ���ƁC
(r/2)*��3 + r*��2 = 1.
����āC
r=2/((��3)+2*��2))=(2/5)*(2*��2 - ��3).
[�lj���� 2]
��ӂ̒����́C((4-3^(1/2))/13)^(1/2) (��)
��ӂ̒�����s�Ƃ���ƁC
|(-s)*(cos(-120��)+i*sin(-120��))+(s*��3)|=1.
����āC
((1/2+��3)*s)^2+((-s*��3)/2)^2=1.
����āC
s=��(1/(4+��3))=��((4-��3)/13).
(�ȏ�)
�����̗��ꁄ�@�@�@�@�@�@�@�@�@�@�@�@�@�@�X�V�@�@11��11��
�ݖ�P
���W���ʏ��,�R�_![]() �̍��W��
�̍��W��![]() �Ƃ����B
�Ƃ����B
�����@�R�_![]() �̂Ƃ�,
�̂Ƃ�,
�O�p�`�̖ʐς�![]() �𗘗p����Ɓ@
�𗘗p����Ɓ@
�O�p�`�`�a�b�̖ʐςr��![]()
������,�����n�`�̕�������![]() ����,�p�̍��W��
����,�p�̍��W��![]() �ƂȂ�B
�ƂȂ�B
�����,�O�p�`�p�a�o�̖ʐςs�͂s��![]()
�@��ӂ���,�Q�s���r���,�������Q���Q�@�E�E�E�@
���,�`�a��������,���Q�{���Q�����Q�@�E�E�E�A
�@�@�`�b��������,�i���|���j�Q�{���Q�����Q�@�E�E�E�B
�A�\�B����,�Q���������Q�{���Q�|���Q�@�E�E�E�C
�@���C�ɑ������,�@�S���Q�����Q�{���Q�|���Q�@
���@![]() �@�@��
�@�@��
�u���̗���v �@�@�@�@�@�@�@�@�@�@�@�@�@�@
�X�V 11/11

�u �W���J�[�v����,���̊ȒP�ȏؖ��������Ă��܂����B
�i�ؖ��j
��ABC�̓��ډ~��AB�CBC�CCA�Ƃ̐ړ_��D�CE�CF�Ƃ���B
BD��BE��a-r�CAD��AF��b-r
AB=BD+AD���Cc=(a-r)+(b-r)
��c=a+b-2r�@�i�I�j
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���, �ƃy���l�[����Y����, ���[���ő����Ă��������B�҂��Ă��܂��B
