—كکa‚T”N‚RŒژ‚V“ْ
 [—¬‚êگ¯]
[—¬‚êگ¯]
پ@پ@‘و423‰ٌگ”ٹw“I‚بکA‘±‰•ه‰ً“ڑ
پ@پ@پ@پ@پƒ‰ً“ڑ•هڈWٹْٹشپF‚QŒژ‚T“ْپ`‚RŒژ‚T“ْپ„
پmڈè—]‚جژüٹْگ«پn
گ®ژ®f(x)پپ‚ک‚چ‚ًگ®ژ®P‚ژ(x)‚إٹ„‚ء‚½ڈ¤‚ًQ‚ژ(x)پC—]‚è‚ًR‚ژ(x)‚ئ‚·‚éپB
‚½‚¾‚µپC‚چپC‚ژ‚حژ©‘Rگ”پCQ‚ژ(x)پپ0‚à‰آ‚ئ‚·‚éپB
–â‚Pپ@‚چپپ2023‚ج‚ئ‚«پCژں‚ج–â‚ة“ڑ‚¦‚وپB
پi‚PپjP‚P(x)پپ‚ک‚Qپ{‚P‚ج‚ئ‚«پCR‚P(x)‚ً‹پ‚ك‚وپB
پi‚QپjP‚Q(x)پپ‚ک‚Qپ{‚کپ{‚P‚ج‚ئ‚«پCR2(x)‚ً‹پ‚ك‚وپB
پi‚RپjP‚R(x)پپ‚ک‚Rپ{‚ک‚Qپ{‚کپ{‚P‚ج‚ئ‚«پCR3(x)‚ً‹پ‚ك‚وپB
پi‚SپjP‚S(x)پپ‚ک‚Sپ{‚ک‚Qپ{‚P‚ج‚ئ‚«پCR4(x)‚ً‹پ‚ك‚وپB
پi‚TپjP‚T(x)پپ‚ک‚Sپ{‚P‚ج‚ئ‚«پCR5(x)‚ً‹پ‚ك‚وپB
پi‚UپjP‚U(x)پپ‚ک‚Sپ{‚ک‚Rپ{‚ک‚Qپ{‚کپ{‚P‚ج‚ئ‚«پCR‚U(x)‚ً‹پ‚ك‚وپB
–â‚Qپ@R‚ژ(x)‚جژüٹْگ«‚ً”Œ©‚µ‚ؤپCژں‚ج–â‚ة“ڑ‚¦‚وپB
پi‚PپjR‚P(x)پپR‚R(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
پi‚QپjR‚Q(x)پپR‚S(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
پi‚RپjR‚R(x)پپR‚T(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
پi‚SپjR‚S(x)پپR‚U(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
پi‚TپjR‚P(x)پپR‚Q(x)پپR‚R(x)پپR‚S(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
پi‚UپjR‚P(x)پپR‚Q(x)پپR‚R(x)پپR‚S(x)پپR‚T(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
پi‚VپjR‚P(x)پپR‚Q(x)پپR‚R(x)پپR‚S(x)پپR‚T(x) پپR‚U(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
ژQچl‚ة‚µ‚½‰ك‹ژ‚ج‘هٹw“üژژ–â‘è‚إ‚·پB
2021”N‘پˆî“c‘هٹw‚إ‚حx2021‚ًx‚Sپ\‚ک‚Qپ{‚P‚إٹ„‚ء‚½—]‚è‚ً‹پ‚ك‚وپB
2004”N‘ه•ھ‘هٹw‚إ‚ح‚ژ‚ًگ³‚جگ®گ”‚ئ‚·‚éپBگ®ژ®‚ک‚ژ‚ً‚ک‚Tپ|‚P‚إٹ„‚ء‚½—]‚è‚ً‹پ‚ك‚وپB
’ا‰ء–â‘è‚Pپiڈo‘èژز‚حپuƒWƒ‡پ[ƒJپ[پvپj
‘و417‰ٌ‚©‚ç‚جپuگ³ژOٹpŒ`‚ج•س‚â‰~Œت‚ة‚و‚ء‚ؤˆح‚ـ‚ꂽگ}Œ`“à‚ج‚S‰~پv
ƒVƒٹپ[ƒY‚ج‘و‚T–â–ع‚ة‚ب‚è‚ـ‚·پB
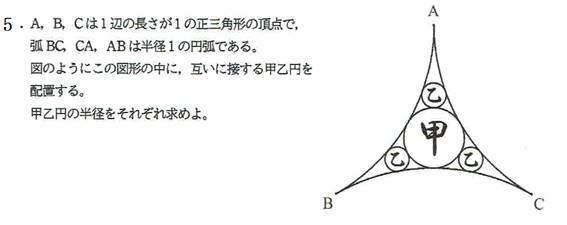
’ا‰ء–â‘è‚Q
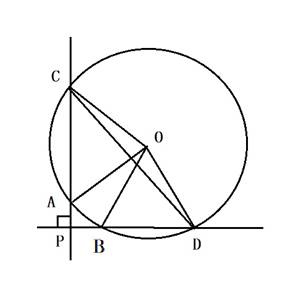
گ}‚ج‚و‚¤‚ةپC‰~O‚ة‚Q’¼گüPAC‚ئPBD‚ھگ‚’¼‚ةŒً‚ي‚ء‚ؤ‚¢‚é‚ئ‚«پCپ¢OAB‚ئپ¢OCD‚ج–تگد‚ھ“™‚µ‚¢‚±‚ئ‚ًڈط–¾‚¹‚وپB
‚½‚¾‚µپC“_P‚ح‰~ٹO‚ة‚ ‚èپC“_O‚ح‰~O‚ج’†گS‚ئ‚·‚éپB
پ@
 ڈo“TپuƒpƒYƒ‹‚إ‚ذ‚ç‚ك‚•âڈ•گü‚جٹô‰½ٹwپv’†‘؛‹`چى’کپ@
ڈo“TپuƒpƒYƒ‹‚إ‚ذ‚ç‚ك‚•âڈ•گü‚جٹô‰½ٹwپv’†‘؛‹`چى’کپ@
BLUE BACKS
NO1پuƒWƒ‡پ[ƒJپ[پv پ@02/04 پ@پ@
17ژ03•ھ ژَگM چXگV 3/5
چ،“ْ‚جژ“_‚إ–â‘è‚ھUp‚³‚ê‚ؤ‚¢‚½‚ج‚إپC‰•ه‚µ‚ـ‚·پB
ٹٌ‚¹‚ç‚ꂽ–â‘è‚ج‰ً“ڑ‚إ‚·
پuƒWƒ‡پ[ƒJپ[پv پ@02/04 پ@پ@
18ژ51•ھ ژَگM چXگV 3/5
ٹٌ‚¹‚ç‚ꂽ’ا‰ء–â‘è‚ج‰ً“ڑ‚إ‚·
پuƒWƒ‡پ[ƒJپ[پv پ@02/08 پ@پ@
06ژ05•ھ ژَگM چXگV 3/5
ٹٌ‚¹‚ç‚ꂽژQچl‚ة‚µ‚½‘هٹw“üژژ–â‘è‚ج‰ً“ڑ‚إ‚·
NO2پukasamaپv 02/07
00ژ04•ھپ@ ژَگM چXگV 3/5
ٹٌ‚¹‚ç‚ꂽ–â‘è‚ج‰ً“ڑ‚إ‚·
پukasamaپv
02/08
01ژ37•ھپ@ ژَگM چXگV 3/5
پ@ٹٌ‚¹‚ç‚ꂽ’ا‰ء–â‘è‚ج‰ً“ڑ‚إ‚·
NO3پuƒXƒ‚پ[ƒNƒ}ƒ“پv 02/07
20ژ01•ھپ@ ژَگM چXگV 3/5
’ا‰ء–â‘è‚Pپiڈo‘èژز‚حپuƒWƒ‡پ[ƒJپ[پvپj
‘و417‰ٌ‚©‚ç‚جپuگ³ژOٹpŒ`‚ج•س‚â‰~Œت‚ة‚و‚ء‚ؤˆح‚ـ‚ꂽگ}Œ`“à‚ج‚S‰~پv
ƒVƒٹپ[ƒY‚ج‘و‚T–â–ع‚ة‚ب‚è‚ـ‚·پBپ@
‰ٌ“ڑ
1•س2‚جگ³ژOٹpŒ`‚ج’†‚ج1•س1‚جگ³ژOٹpŒ`‚إپc
ٹO‘¤‚ج‘ه‚«‚بگ³ژOٹpŒ`‚جچ‚‚³=پم3
’¸“_‚©‚çڈdگS‚ـ‚إ‚ج‹——£=(2پم3/3)
Soپcچb‚ج”¼ŒaR=2پم3/3-1=(2پم3-3)/3پ@=0.1547پc
‰³‚ج”¼Œa‚ًr‚ئ‚·‚é‚ئپc
•û‚ׂ«‚ج’è—‚و‚èپc
(پم3/3-R-r)^2=r*(2+r)
((3-پم3)/3-r)^2=r*(2+r)
(3-پم3)^2/9=(2+2(3-پم3)/3)*r
r=(9-4پم3)/33پ@=0.062پc
’ا‰ء–â‘è‚Q
گ}‚ج‚و‚¤‚ةپC‰~O‚ة‚Q’¼گüPAC‚ئPBD‚ھگ‚’¼‚ةŒً‚ي‚ء‚ؤ‚¢‚é‚ئ‚«پCپ¢OAB‚ئپ¢OCD‚ج–تگد‚ھ“™‚µ‚¢‚±‚ئ‚ًڈط–¾‚¹‚وپB
‚½‚¾‚µپC“_P‚ح‰~ٹO‚ة‚ ‚èپC“_O‚ح‰~O‚ج’†گS‚ئ‚·‚éپB
پuƒXƒ‚پ[ƒNƒ}ƒ“پv 02/12
19ژ02•ھپ@ ژَگM چXگV 3/5
–â1
(6پjP‚U(x)پپ‚ک‚Sپ{‚ک‚Rپ{‚ک‚Qپ{‚کپ{‚P‚ج‚ئ‚«پCR‚U(x)‚ً‹پ‚ك‚وپB
f(x)=x^2023=(x^5-1)/(x-1)*Q(6)+a*x^3+b*x^2+c*x+d
x^5-1=0 ‚ج1ˆبٹO‚جچھ‚جˆê‚آ‚ًz‚ئ‚·‚éپc
f(z)=z^3=a*z^3+b*z^2+c*z+d
soپca=1,b=c=d=0
soپc
R6(x)=x^3
‘¼‚à“¯‚¶‚و‚¤‚ةچl‚¦‚ê‚خپc
(1)
P‚P(x)پپ‚ک‚Qپ{‚P‚ج‚ئ‚«پCR‚P(x)‚ً‹پ‚ك‚وپB
f(x)=x^2023=(x^4-1)/(x^2-1)*Q(1)(x)+a*x+b
f(z)=z^3=-z=a*z+b
soپcR1(x)=-x
(2)
P‚Q(x)پپ‚ک‚Qپ{‚کپ{‚P‚ج‚ئ‚«پCR2(x)‚ً‹پ‚ك‚وپB
f(x)=x^2023=(x^2+x+1)*Q(2)(x)+a*x*b
=(x^3-1)/(x-1)*Q2(x)+a*x+b
z^3=1
f(z)=z=a*z+b
soپca=1,b=0
soپcR2(x)=x
(3)
P‚R(x)پپ‚ک‚Rپ{‚ک‚Qپ{‚کپ{‚P‚ج‚ئ‚«پCR3(x)‚ً‹پ‚ك‚وپB
f(x)=(x^3+x^2+x+1)*Q3(x)+a*x^2+b*x+c
=(x^4-1)/(x-1)*Q3(x)+a*x^2+b*x+c
z^4=1
f(z)=z^3=a*z^2+b*z+c=-z^2-z-1
soپc
R3(x)=-x^2-x-1
(4)
P‚S(x)پپ‚ک‚Sپ{‚ک‚Qپ{‚P‚ج‚ئ‚«پCR4(x)‚ً‹پ‚ك‚وپB
f(x)=(x^4+x^3+x^2+x+1)*Q4(x)+a*x^3+b*x^2+c*x+d
=(x^6-1)/(x^2-1)*Q4(x)+a*x^3+b*x^2+c*x+d
z^6=1
f(z)=z=a*z^3+b*z^2+c*z+d
soپc
R4(x)=x
(5)
P‚T(x)پپ‚ک‚Sپ{‚P‚ج‚ئ‚«پCR5(x)‚ً‹پ‚ك‚وپB
f(x)=(x^4+1)*Q5(x)+a*x^3+b*x^2+c*x+d
(x^8-1)/(x^4-1)*Q5(x)+a*x^3+b*x^2+c*x+d
z^4=-1
f(z)=(z^4)^(505)*z^3=-z^3=a*z^3+b*z^2+c*z+d
soپc
R5(x)=-x^3
پuƒXƒ‚پ[ƒNƒ}ƒ“پv 02/20
20ژ52•ھپ@ ژَگM چXگV 3/5
–â2
ˆس–،‚ھ‚و‚’ح‚ك‚ب‚¢‚ج‚إ‚·‚ھپc
ڈم‚ج–â‘è‚ةژ¦‚³‚ê‚ؤ‚¢‚é‚à‚ج‚إچl‚¦‚é‚ئپc
P‚P(x)پپ‚ک‚Qپ{‚P
P‚Q(x)پپ‚ک‚Qپ{‚کپ{‚P
P‚R(x)پپ‚ک‚Rپ{‚ک‚Qپ{‚کپ{‚P
P‚S(x)پپ‚ک‚Sپ{‚ک‚Qپ{‚P
P‚T(x)پپ‚ک‚Sپ{‚P
P‚U(x)پپ‚ک‚Sپ{‚ک‚Rپ{‚ک‚Qپ{‚کپ{‚P
پi21پjR‚P(x)پپR‚R(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
4,4‚جچإڈ¬Œِ”{گ”
ˆب‰؛پAk‚ًژ©‘Rگ”‚ئ‚·‚é
Soپcm=4k
پi22پjR‚Q(x)پپR‚S(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
3,6‚جچإڈ¬Œِ”{گ”
Soپcm=6k
پi23پjR‚R(x)پپR‚T(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
4,8‚جچإڈ¬Œِ”{گ”
Soپcm=8k
پi24پjR‚S(x)پپR‚U(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
6,5‚جچإڈ¬Œِ”{گ”
Soپcm=30k
پi25پjR‚P(x)پپR‚Q(x)پپR‚R(x)پپR‚S(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
4,3,4,6‚جچإڈ¬Œِ”{گ”
Soپcm=12k
پi26پjR‚P(x)پپR‚Q(x)پپR‚R(x)پپR‚S(x)پپR‚T(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
4,3,4,6,8
‚جچإڈ¬Œِ”{گ”
Soپcm=24k
پi27پjR‚P(x)پپR‚Q(x)پپR‚R(x)پپR‚S(x)پپR‚T(x) پپR‚U(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
4,3,4,6,8,5‚جچإڈ¬Œِ”{گ”
Soپcm=120k
پƒگ…‚ج—¬‚êپFڈè—]‚ھˆê’v‚·‚éڈêچ‡‚ح‘¼‚ة‚à‚ ‚è‚ـ‚·پBپ„
پuƒXƒ‚پ[ƒNƒ}ƒ“پv
02/22
10ژ57•ھپ@ ژَگM چXگV 3/5
–â2
ڈم‚ج–â1‚ةژ¦‚³‚ê‚ؤ‚¢‚é‚à‚ج‚إچl‚¦‚é‚ئپc‚ ‚ـ‚è‚جژüٹْ‚ح...
P‚P(x)پپ‚ک‚Qپ{‚PپEپEپE(x^4-1)/(x^2-1)پEپEپEx,-1,-x,1 ‚ج4ژüٹْ
P‚Q(x)پپ‚ک‚Qپ{‚کپ{‚PپEپEپE(x^3-1)/(x-1)پEپEپEx,x^2=-x-1,1 ‚ج3ژüٹْ
P‚R(x)پپ‚ک‚Rپ{‚ک‚Qپ{‚کپ{‚PپEپEپE(x^4-1)/(x-1)پEپEپEx,x^2,(-x^2-x-1),1 ‚ج4ژüٹْ
P‚S(x)پپ‚ک‚Sپ{‚ک‚Qپ{‚PپEپEپE(x^6-1)/(x^2-1)پEپEپEx,x^2,x^3,(-x^2-1),(-x^3-x),1 ‚ج6ژüٹْ
P‚T(x)پپ‚ک‚Sپ{‚PپEپEپE(x^8-1)/(x^4-1)پEپEپEx,x^2,x^3,-1,-x,-x^2,-x^3,1 ‚ج8ژüٹْ
P‚U(x)پپ‚ک‚Sپ{‚ک‚Rپ{‚ک‚Qپ{‚کپ{‚PپEپEپE(x^5-1)/(x-1)پEپEپEx,x^2,x^3,(-x^3-x^2-x-1),1 ‚ج5ژüٹْ
پi21پjR‚P(x)پپR‚R(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
4,4‚جچإڈ¬Œِ”{گ” 4
ˆب‰؛پAk‚ًژ©‘Rگ”‚ئ‚·‚é
x,1‚ھ“¯‚¶‚ب‚ج‚إپc
Soپcm=4k-1,4k
پi22پjR‚Q(x)پپR‚S(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
P‚Q(x)پپ‚ک‚Qپ{‚کپ{‚PپEپEپE(x^3-1)/(x-1)پEپEپEx,(-x-1),1
P‚S(x)پپ‚ک‚Sپ{‚ک‚Qپ{‚PپEپEپE(x^6-1)/(x^2-1)پEپEپEx,x^2,x^3,(-x^2-1),(-x^3-x),1
x,1‚ھ“¯‚¶‚ب‚ج‚إپc
3,6‚جچإڈ¬Œِ”{گ” 6
Soپcm=6k-5,6k
پi23پjR‚R(x)پپR‚T(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
P‚R(x)پپ‚ک‚Rپ{‚ک‚Qپ{‚کپ{‚PپEپEپE(x^4-1)/(x-1)پEپEپEx,x^2,(-x^2-x-1),1
P‚T(x)پپ‚ک‚Sپ{‚PپEپEپE(x^8-1)/(x^4-1)پEپEپEx,x^2,x^3,-1,-x,-x^2,-x^3,1
X,x^2,1‚ھ“¯‚¶
4,8‚جچإڈ¬Œِ”{گ” 8
Soپcm=8k-7,8k-6,8k
پi24پjR‚S(x)پپR‚U(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
P‚S(x)پپ‚ک‚Sپ{‚ک‚Qپ{‚PپEپEپE(x^6-1)/(x^2-1)پEپEپEx,x^2,x^3,(-x^2-1),(-x^3-x),1
P‚U(x)پپ‚ک‚Sپ{‚ک‚Rپ{‚ک‚Qپ{‚کپ{‚PپEپEپE(x^5-1)/(x-1)پEپEپEx,x^2,x^3,(-x^3-x^2-x-1),1
x,x^2,x^3,1‚ھ“¯‚¶پc
6,5‚جچإڈ¬Œِ”{گ” 30
Soپcm=30k-29,30k-28,30k-27,30k
پi25پjR‚P(x)پپR‚Q(x)پپR‚R(x)پپR‚S(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
P‚P(x)پپ‚ک‚Qپ{‚PپEپEپE(x^4-1)/(x^2-1)پEپEپEx,-1,-x,1
P‚Q(x)پپ‚ک‚Qپ{‚کپ{‚PپEپEپE(x^3-1)/(x-1)پEپEپEx,x^2=-x-1,1
P‚R(x)پپ‚ک‚Rپ{‚ک‚Qپ{‚کپ{‚PپEپEپE(x^4-1)/(x-1)پEپEپEx,x^2,(-x^2-x-1),1
P‚S(x)پپ‚ک‚Sپ{‚ک‚Qپ{‚PپEپEپE(x^6-1)/(x^2-1)پEپEپEx,x^2,x^3,-x^2-1,-x^3-x,1
x,1 ‚ھ“¯‚¶پc
4,3,4,6‚جچإڈ¬Œِ”{گ” 12
Soپcm=12k-11,12k
پi26پjR‚P(x)پپR‚Q(x)پپR‚R(x)پپR‚S(x)پپR‚T(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
P‚P(x)پپ‚ک‚Qپ{‚PپEپEپE(x^4-1)/(x^2-1)پEپEپEx,-1,-x,1
P‚Q(x)پپ‚ک‚Qپ{‚کپ{‚PپEپEپE(x^3-1)/(x-1)پEپEپEx,x^2=-x-1,1
P‚R(x)پپ‚ک‚Rپ{‚ک‚Qپ{‚کپ{‚PپEپEپE(x^4-1)/(x-1)پEپEپEx,x^2,(-x^2-x-1),1
P‚S(x)پپ‚ک‚Sپ{‚ک‚Qپ{‚PپEپEپE(x^6-1)/(x^2-1)پEپEپEx,x^2,x^3,-x^2-1,-x^3-x,1
P‚T(x)پپ‚ک‚Sپ{‚PپEپEپE(x^8-1)/(x^4-1)پEپEپEx,x^2,x^3,-1,-x,-x^2,-x^3,1
x,1‚ھ“¯‚¶پc
4,3,4,6,8 ‚جچإڈ¬Œِ”{گ” 24
Soپcm=24k-23,24k
پi27پjR‚P(x)پپR‚Q(x)پپR‚R(x)پپR‚S(x)پپR‚T(x)پپR‚U(x)‚ئ‚ب‚é‚چ‚ج’l‚ً‹پ‚ك‚وپB
P‚P(x)پپ‚ک‚Qپ{‚PپEپEپE(x^4-1)/(x^2-1)پEپEپEx,-1,-x,1
P‚Q(x)پپ‚ک‚Qپ{‚کپ{‚PپEپEپE(x^3-1)/(x-1)پEپEپEx,x^2=-x-1,1
P‚R(x)پپ‚ک‚Rپ{‚ک‚Qپ{‚کپ{‚PپEپEپE(x^4-1)/(x-1)پEپEپEx,x^2,(-x^2-x-1),1
P‚S(x)پپ‚ک‚Sپ{‚ک‚Qپ{‚PپEپEپE(x^6-1)/(x^2-1)پEپEپEx,x^2,x^3,-x^2-1,-x^3-x,1
P‚T(x)پپ‚ک‚Sپ{‚PپEپEپE(x^8-1)/(x^4-1)پEپEپEx,x^2,x^3,-1,-x,-x^2,-x^3,1
P‚U(x)پپ‚ک‚Sپ{‚ک‚Rپ{‚ک‚Qپ{‚کپ{‚PپEپEپE(x^5-1)/(x-1)پEپEپEx,x^2,x^3,(-x^3-x^2-x-1),1
x,1‚ھ“¯‚¶پc
4,3,4,6,8,5‚جچإڈ¬Œِ”{گ” 120
Soپcm=120k-119,120k
NO4پu‚و‚س‚©‚µ‚ج‚آ‚ç‚¢‚¨‚¶‚³‚ٌپv2/13 17ژ20•ھ ژَگM چXگV 3/5
–â1
پœ ٹePn(x)‚ً0‚ئ‚·‚é‚ک‚ً’²‚ׂـ‚·پB
پE![]() پi-1‚ج•½•ûچھپj
پi-1‚ج•½•ûچھپj
پE![]()
![]() (1‚ج—§•ûچھ‚إ1‚إ‚ب‚¢‚à‚ج)
(1‚ج—§•ûچھ‚إ1‚إ‚ب‚¢‚à‚ج)
پE![]()
![]() (1‚ج4ڈوچھ‚إ1‚إ‚ب‚¢‚à‚ج)
(1‚ج4ڈوچھ‚إ1‚إ‚ب‚¢‚à‚ج)
پE![]()
![]()
![]()
(1‚ج3ڈوچھ‚إ1‚إ‚ب‚¢‚à‚ج‚ئپA-1‚ج3ڈوچھ‚إ -1‚إ‚ب‚¢‚à‚ج
‚آ‚ـ‚èپA1‚ج6ڈوچھ‚إپ}1‚إ‚ب‚¢‚à‚ج)
پE![]() پi-1‚ج4ڈوچھپj
پi-1‚ج4ڈوچھپj
پE![]()
P6(x)‚ً0‚ئ‚·‚é‚ک‚حپA1‚ج5ڈوچھ‚إپA1ˆبٹO‚ج‚à‚ج‚إ‚·پB
پ@360پ€5پپ72‚ب‚ج‚إپA![]() ‚إ‚·پBپikپپ1,2,3,4پj
‚إ‚·پBپikپپ1,2,3,4پj
پ@‚½‚¾‚µپA‚±‚ê‚إŒvژZ‚·‚é‚ئ–ت“|‚إ‚·پB
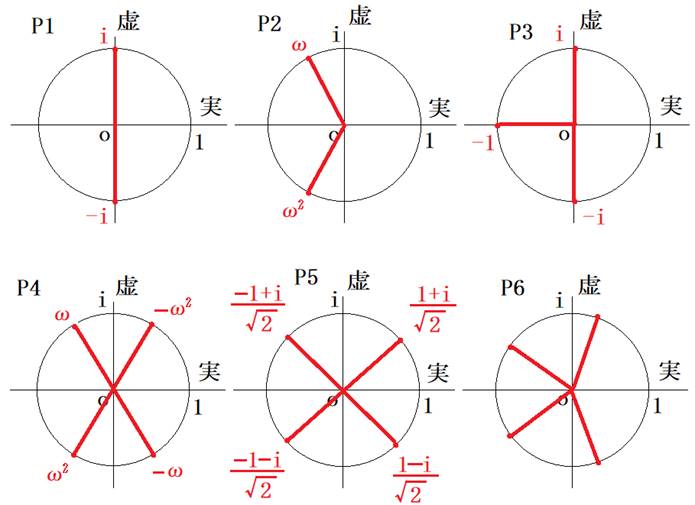
پœ![]() ‚إ
‚إ ![]() ‚ئ‚ب‚é
‚ئ‚ب‚é ![]() ‚ً‘م“ü‚µ‚ـ‚·پB
‚ً‘م“ü‚µ‚ـ‚·پB
‚·‚é‚ئپA![]()
‚±‚جŒم‚حپA‚±‚ج‰؛گü‚جژ®(*)‚إچl‚¦‚ـ‚·پB
(1) ![]() ‚حپA4ڈو‚·‚é‚ئپA1‚ة‚ب‚é‚ج‚إپA
‚حپA4ڈو‚·‚é‚ئپA1‚ة‚ب‚é‚ج‚إپA
![]()
‚ـ‚½پA![]() ‚حپA2ژںژ®‚ب‚ج‚إپA
‚حپA2ژںژ®‚ب‚ج‚إپA![]() ‚ئ‚µ‚ـ‚·پB
‚ئ‚µ‚ـ‚·پB
![]()
(2) ![]() ‚حپA3ڈو‚·‚é‚ئپA1‚ة‚ب‚é‚ج‚إپA
‚حپA3ڈو‚·‚é‚ئپA1‚ة‚ب‚é‚ج‚إپA
![]()
‚ـ‚½پA![]() ‚حپA2ژںژ®‚ب‚ج‚إپA
‚حپA2ژںژ®‚ب‚ج‚إپA![]() ‚ئ‚µ‚ـ‚·پB
‚ئ‚µ‚ـ‚·پB
![]()
(3) ![]() ‚حپA4ڈو‚·‚é‚ئپA1‚ة‚ب‚é‚ج‚إپA
‚حپA4ڈو‚·‚é‚ئپA1‚ة‚ب‚é‚ج‚إپA
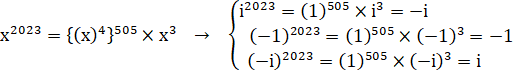
‚ـ‚½پA![]() ‚حپA3ژںژ®‚ب‚ج‚إپA
‚حپA3ژںژ®‚ب‚ج‚إپA![]() ‚ئ‚µ‚ـ‚·پB
‚ئ‚µ‚ـ‚·پB
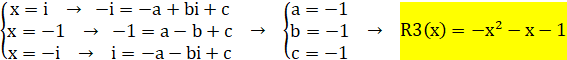
(4) ![]() ‚حپA6ڈو‚·‚é‚ئپA1‚ة‚ب‚é‚ج‚إپA
‚حپA6ڈو‚·‚é‚ئپA1‚ة‚ب‚é‚ج‚إپA
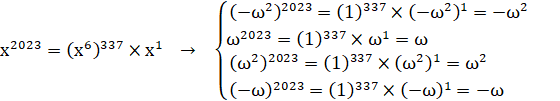
‚ـ‚½پA![]() ‚حپA4ژںژ®‚ب‚ج‚إپA
‚حپA4ژںژ®‚ب‚ج‚إپA![]() ‚ئ‚µ‚ـ‚·پB
‚ئ‚µ‚ـ‚·پB
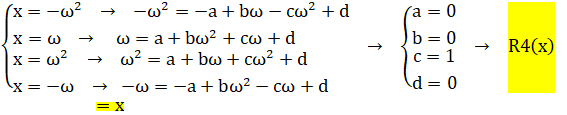
(5) ![]() ‚حپA8ڈو‚·‚é‚ئپA1‚ة‚ب‚é‚ج‚إپA
‚حپA8ڈو‚·‚é‚ئپA1‚ة‚ب‚é‚ج‚إپA
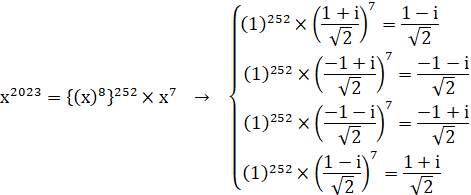
‚ـ‚½پA![]() ‚حپA4ژںژ®‚ب‚ج‚إپA
‚حپA4ژںژ®‚ب‚ج‚إپA![]() ‚ئ‚µ‚ـ‚·پB
‚ئ‚µ‚ـ‚·پB

(6) ![]() ‚إ‚·پB
‚إ‚·پB
![]() ‚ًˆê‚ـ‚ئ‚ك‚ة‚µ‚ؤچl‚¦‚ـ‚·پB
‚ًˆê‚ـ‚ئ‚ك‚ة‚µ‚ؤچl‚¦‚ـ‚·پB
![]() ‚ب‚ج‚إپA
‚ب‚ج‚إپA
‚ـ‚¸پA![]() ‚ً
‚ً![]() ‚إٹ„‚邱‚ئ‚ًچl‚¦‚ـ‚·پB
‚إٹ„‚邱‚ئ‚ًچl‚¦‚ـ‚·پB
![]()
‚ئ‚·‚é‚ئپA1ژںژ® ![]() ‚إٹ„‚é‚ج‚إپA—]‚èR‚ح’èگ”‚ة‚ب‚è‚ـ‚·پB
‚إٹ„‚é‚ج‚إپA—]‚èR‚ح’èگ”‚ة‚ب‚è‚ـ‚·پB
![]() ‚ئ‚·‚é‚ئپA
‚ئ‚·‚é‚ئپA![]()
‚ن‚¦‚ةپA
![]()
![]()
—¼•س‚ً![]() ”{‚·‚é‚ئپA
”{‚·‚é‚ئپA
![]()
![]()
‚ئ‚ب‚é‚ج‚إپA—]‚è ![]() ‚إ‚·پB
‚إ‚·پB
پu‚و‚س‚©‚µ‚ج‚آ‚ç‚¢‚¨‚¶‚³‚ٌپv2/14 20ژ05•ھ ژَگM چXگV 3/5
–â2
پœPn(x)‚ً0‚ئ‚·‚é‚ک‚حپA1‚ج‚ׂ«ڈوچھ‚ب‚ج‚إپA![]() ‚ج’l‚حژüٹْ“I‚ة“¯‚¶’l‚ًŒJ‚è•ش‚µ‚ـ‚·پB
‚ج’l‚حژüٹْ“I‚ة“¯‚¶’l‚ًŒJ‚è•ش‚µ‚ـ‚·پB
‚چپپ1‚ج‚ئ‚«‚حپA![]() ‚إ‚·پB
‚إ‚·پB
پE
![]() ‚ً0‚ئ‚·‚é
‚ً0‚ئ‚·‚é![]() ‚حپA4ڈو‚·‚é‚ئپA1‚ة‚ب‚è‚ـ‚·پB
‚حپA4ڈو‚·‚é‚ئپA1‚ة‚ب‚è‚ـ‚·پB
پ@![]() ‚حپA‚چ‚ھ4‘‚¦‚é‚ئ“¯‚¶’l‚ً‚ئ‚è‚ـ‚·پB
‚حپA‚چ‚ھ4‘‚¦‚é‚ئ“¯‚¶’l‚ً‚ئ‚è‚ـ‚·پB
(*)‚جژ® ![]() ‚إچl‚¦‚ـ‚·پB
‚إچl‚¦‚ـ‚·پB
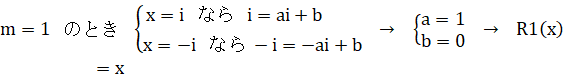
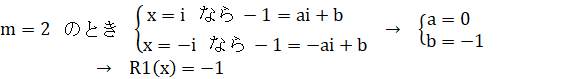
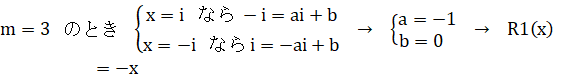
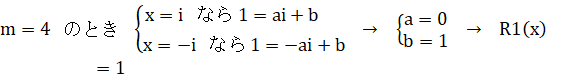
![]() ‚حپA
‚حپA![]() ‚ًŒJ‚è•ش‚µ‚ـ‚·پB
‚ًŒJ‚è•ش‚µ‚ـ‚·پB
پœڈم‚ج‚â‚è•û‚حپAڈêچ‡‚جگ”‚ھ‘½‚ŒvژZ‚ھ–ت“|‚إ‚·پB
•ت‚ج•û–@‚ًچl‚¦‚ـ‚·پB
پE![]() ‚ً0‚ئ‚·‚é
‚ً0‚ئ‚·‚é![]() ‚حپA4ڈو‚·‚é‚ئپA1‚ة‚ب‚è‚ـ‚·پB
‚حپA4ڈو‚·‚é‚ئپA1‚ة‚ب‚è‚ـ‚·پB
‚آ‚ـ‚èپA![]() ‚حپA‚چ‚ھ4‘‚¦‚é‚ئ“¯‚¶’l‚ً‚ئ‚è‚ـ‚·پB
‚حپA‚چ‚ھ4‘‚¦‚é‚ئ“¯‚¶’l‚ً‚ئ‚è‚ـ‚·پB
![]() ‚جŒ`‚ًچl‚¦‚ـ‚·پB
‚جŒ`‚ًچl‚¦‚ـ‚·پB
‚چ‚ھ1‚©‚çژn‚ك‚ؤپA‚ک”{‚µ‚ؤ‚¢‚‚ئپA
![]()
![]()
![]()
![]()
‚آ‚ـ‚èپA![]() ‚حپA
‚حپA![]() ‚ًŒJ‚è•ش‚µ‚ـ‚·پB
‚ًŒJ‚è•ش‚µ‚ـ‚·پB
ڈم‚جŒ‹‰ت‚ئ“¯‚¶‚ة‚ب‚è‚ـ‚µ‚½پB
پE![]() ‚ً0‚ئ‚·‚é
‚ً0‚ئ‚·‚é![]() ‚حپA3ڈو‚·‚é‚ئپA1‚ة‚ب‚è‚ـ‚·پB
‚حپA3ڈو‚·‚é‚ئپA1‚ة‚ب‚è‚ـ‚·پB
‚آ‚ـ‚èپA![]() ‚حپA‚چ‚ھ3‘‚¦‚é‚ئ“¯‚¶’l‚ً‚ئ‚è‚ـ‚·پB
‚حپA‚چ‚ھ3‘‚¦‚é‚ئ“¯‚¶’l‚ً‚ئ‚è‚ـ‚·پB
![]() ‚جŒ`‚ة•دŒ`‚·‚é‚ئپA
‚جŒ`‚ة•دŒ`‚·‚é‚ئپA
‚چ‚ھ1‚©‚çژn‚ك‚ؤپA‚ک”{‚µ‚ؤ‚¢‚‚ئپA
![]()
![]()
![]()
‚آ‚ـ‚èپA![]() ‚حپA
‚حپA![]() ‚ًŒJ‚è•ش‚µ‚ـ‚·پB
‚ًŒJ‚è•ش‚µ‚ـ‚·پB
پE![]() ‚ً0‚ئ‚·‚é
‚ً0‚ئ‚·‚é![]() ‚حپA4ڈو‚·‚é‚ئپA1‚ة‚ب‚è‚ـ‚·پB
‚حپA4ڈو‚·‚é‚ئپA1‚ة‚ب‚è‚ـ‚·پB
‚آ‚ـ‚èپA![]() ‚حپA‚چ‚ھ4‘‚¦‚é‚ئ“¯‚¶’l‚ً‚ئ‚è‚ـ‚·پB
‚حپA‚چ‚ھ4‘‚¦‚é‚ئ“¯‚¶’l‚ً‚ئ‚è‚ـ‚·پB
![]() ‚جŒ`‚ة•دŒ`‚·‚é‚ئپA
‚جŒ`‚ة•دŒ`‚·‚é‚ئپA
‚چ‚ھ1‚©‚çژn‚ك‚ؤپA‚ک”{‚µ‚ؤ‚¢‚‚ئپA
![]()
![]()
![]()
![]()
‚آ‚ـ‚èپA![]() ‚حپA
‚حپA![]() ‚ًŒJ‚è•ش‚µ‚ـ‚·پB
‚ًŒJ‚è•ش‚µ‚ـ‚·پB
پE![]() ‚ً0‚ئ‚·‚é
‚ً0‚ئ‚·‚é![]() ‚حپA6ڈو‚·‚é‚ئپA1‚ة‚ب‚è‚ـ‚·پB
‚حپA6ڈو‚·‚é‚ئپA1‚ة‚ب‚è‚ـ‚·پB
‚آ‚ـ‚èپA![]() ‚حپA‚چ‚ھ6‘‚¦‚é‚ئ“¯‚¶’l‚ً‚ئ‚è‚ـ‚·پB
‚حپA‚چ‚ھ6‘‚¦‚é‚ئ“¯‚¶’l‚ً‚ئ‚è‚ـ‚·پB
پiƒض‚حپA‚چ‚ھ3‘‚¦‚é‚ئ“¯‚¶’l‚ً‚ئ‚è‚ـ‚·‚ھپj
![]() ‚جŒ`‚ة•دŒ`‚·‚é‚ئپA
‚جŒ`‚ة•دŒ`‚·‚é‚ئپA
‚چ‚ھ1‚©‚çژn‚ك‚ؤپA‚ک”{‚µ‚ؤ‚¢‚‚ئپA
![]()
![]()
![]()
![]()
![]()
![]()
‚آ‚ـ‚èپA![]() ‚حپA
‚حپA![]() ‚ًŒJ‚è•ش‚µ‚ـ‚·پB
‚ًŒJ‚è•ش‚µ‚ـ‚·پB
پE![]() ‚ً0‚ئ‚·‚é
‚ً0‚ئ‚·‚é![]() ‚حپA8ڈو‚·‚é‚ئپA1‚ة‚ب‚è‚ـ‚·پB
‚حپA8ڈو‚·‚é‚ئپA1‚ة‚ب‚è‚ـ‚·پB
‚آ‚ـ‚èپA![]() ‚حپA‚چ‚ھ8‘‚¦‚é‚ئ“¯‚¶’l‚ً‚ئ‚è‚ـ‚·پB
‚حپA‚چ‚ھ8‘‚¦‚é‚ئ“¯‚¶’l‚ً‚ئ‚è‚ـ‚·پB
![]() ‚جŒ`‚ة•دŒ`‚·‚é‚ئپA
‚جŒ`‚ة•دŒ`‚·‚é‚ئپA
‚چ‚ھ1‚©‚çژn‚ك‚ؤپA‚ک”{‚µ‚ؤ‚¢‚‚ئپA
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
‚آ‚ـ‚èپA![]() ‚حپA
‚حپA![]() ‚ًŒJ‚è•ش‚µ‚ـ‚·پB
‚ًŒJ‚è•ش‚µ‚ـ‚·پB
پE![]() ‚ً0‚ئ‚·‚é
‚ً0‚ئ‚·‚é![]() ‚حپA5ڈو‚·‚é‚ئپA1‚ة‚ب‚è‚ـ‚·پB
‚حپA5ڈو‚·‚é‚ئپA1‚ة‚ب‚è‚ـ‚·پB
‚آ‚ـ‚èپA![]() ‚حپA‚چ‚ھ5‘‚¦‚é‚ئ“¯‚¶’l‚ً‚ئ‚è‚ـ‚·پB
‚حپA‚چ‚ھ5‘‚¦‚é‚ئ“¯‚¶’l‚ً‚ئ‚è‚ـ‚·پB
![]() ‚جŒ`‚ة•دŒ`‚·‚é‚ئپA
‚جŒ`‚ة•دŒ`‚·‚é‚ئپA
‚چ‚ھ1‚©‚çژn‚ك‚ؤپA‚ک”{‚µ‚ؤ‚¢‚‚ئپA
![]()
![]()
![]()
![]()
‚آ‚ـ‚èپA![]() ‚حپA
‚حپA![]() ‚ًŒJ‚è•ش‚µ‚ـ‚·پB
‚ًŒJ‚è•ش‚µ‚ـ‚·پB
‚ـ‚ئ‚ك‚é‚ئپA
![]() ‚حپAژüٹْ‚ھ4‚إپA
‚حپAژüٹْ‚ھ4‚إپA![]() پA
پA
![]() ‚حپAژüٹْ‚ھ3‚إپA
‚حپAژüٹْ‚ھ3‚إپA![]() پA
پA
![]() ‚حپAژüٹْ‚ھ4‚إپA
‚حپAژüٹْ‚ھ4‚إپA![]() پA
پA
![]() ‚حپAژüٹْ‚ھ6‚إپA
‚حپAژüٹْ‚ھ6‚إپA![]() پA
پA
![]() ‚حپAژüٹْ‚ھ8‚إپA
‚حپAژüٹْ‚ھ8‚إپA![]()
![]() ‚حپAژüٹْ‚ھ5‚إپA
‚حپAژüٹْ‚ھ5‚إپA![]()
ˆبڈم‚©‚ç‚‹‚ًژ©‘Rگ”‚ئ‚µ‚ؤپA
(1)R1(x)پپR3(x)‚ئ‚ب‚é‚ج‚حپA‚ئ‚à‚ةژüٹْ‚ھ4‚ب‚ج‚إپA
‚چپپ4(‚‹پ|1)پ{‚PپA4k
(2)R2(x)پپR4(x)‚ئ‚ب‚é‚ج‚حپA3‚ئ6‚جچإڈ¬Œِ”{گ”‚ًچl‚¦‚ؤپA
‚چپپ6(‚‹پ|1)پ{1پA6‚‹
(3)R3(x)پپR5(x)‚ئ‚ب‚é‚ج‚حپA4‚ئ8‚جچإڈ¬Œِ”{گ”‚ًچl‚¦‚ؤپA
‚چپپ8(‚‹پ|1)پ{1پA8(‚‹پ|1)پ{2پA8‚‹
(4)R4(x)پپR6(x)‚ئ‚ب‚é‚ج‚حپA6‚ئ5‚جچإڈ¬Œِ”{گ”‚ًچl‚¦‚¦‚ؤپA
‚چپپ30(‚‹پ|1)پ{1پA30(‚‹پ|1)پ{2پA30(‚‹پ|1)پ{3پA30‚‹
(5)R1(x)پپR2(x)پپR3(x)پپR4(x)‚ئ‚ب‚é‚ج‚حپA4پA3پA4پA6‚جچإڈ¬Œِ”{گ”‚ًچl‚¦‚ؤپA
‚چپپ12(‚‹پ|1)پ{1پA12‚‹
(6)R1(x)پپR2(x)پپR3(x)پپR4(x)پپR5(x)‚ئ‚ب‚é‚ج‚حپA4پA3پA4پA6پA8‚جچإڈ¬Œِ”{گ”‚ًچl‚¦‚ؤپA
‚چپپ24(‚‹پ|1)پ{1پA24‚‹
(7)R1(x)پپR2(x)پپR3(x)پپR4(x)پپR5(x)پپR6(x)‚ئ‚ب‚é‚ج‚حپA4پA3پA4پA6پA8پA5‚جچإڈ¬Œِ”{گ”‚ًچl‚¦‚ؤپA
‚چپپ120(‚‹پ|1)پ{1پA120‚‹
’ا‰ء–â‘è1
پœ‰EڈمپAچ¶ڈمپA‰؛‚جٹe‰~‚ج’†گS‚ً‚»‚ꂼ‚ê‚`پA‚aپA‚b‚ئ‚µ‚ـ‚·پB
پ¢‚`‚a‚b‚حگ³ژOٹpŒ`‚إ‰~چb‚ج’†گS‚j‚حپAپ¢‚`‚a‚b‚ج’†گü‚جŒً“_‚ب‚ج‚إڈdگS‚إ‚·پB
ڈdگS‚ح’†گü‚ج’¸“_‚ج•û‚©‚ç2پF1‚ج“à•ھ“_‚إ‚·پB
پ¢‚`‚a‚b‚ج1•س‚ج’·‚³‚ھ2‚ب‚ج‚إپA’†گü ![]() ‚إ‚·پB
‚إ‚·پB
‚·‚é‚ئپA
![]() ‚ب‚ج‚إپA‰~چb‚ج”¼Œa‚‹‚حپA
‚ب‚ج‚إپA‰~چb‚ج”¼Œa‚‹‚حپA![]() ‚إ‚·پB
‚إ‚·پB
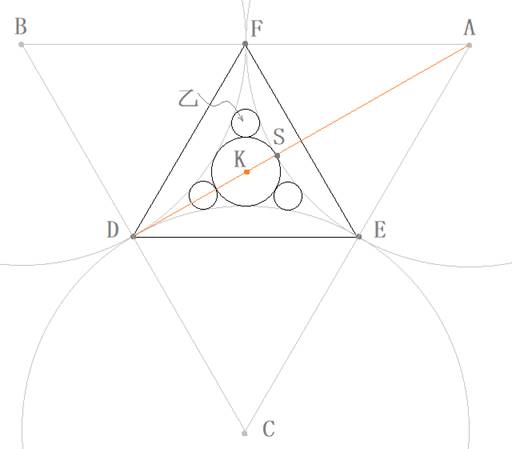
پœ‰~‚`پA‚aپAچbپA‰³‚حŒف‚¢‚ةگع‚µ‚ؤ‚¢‚é‚ج‚إپAƒfƒJƒ‹ƒg‚ج‰~’è—‚ًژg‚¢‚ـ‚·پB
‰~‚`پA‚a‚ج”¼Œa‚ح1پA‰~چb‚ج”¼Œa‚ح
![]() پA‰~‰³‚ج”¼Œa‚ً‚’‚ئ‚·‚é‚ئپA
پA‰~‰³‚ج”¼Œa‚ً‚’‚ئ‚·‚é‚ئپA
![]()
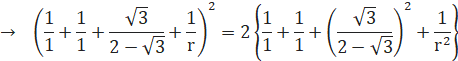
![]()
![]()
![]()
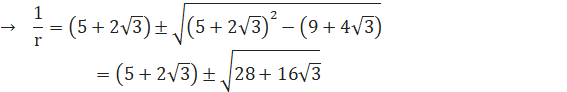
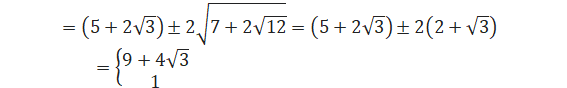
1‚ح•s“K‚ب‚ج‚إپA
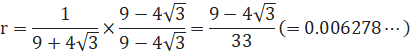
’ا‰ء–â‘è‚Q
پœ2‚آ‚جژOٹpŒ`‚ج–تگد‚حپAژں‚جژ®‚إ•\‚¹‚ـ‚·پB
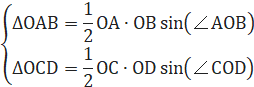
–تگد‚جŒvژZ‚ةژg‚¤•س‚ج’·‚³‚حپA‰~‚ج”¼Œa‚إ‚·‚ׂؤ“™‚µ‚¢‚إ‚·پB
![]() ‚ب‚ج‚إپA
‚ب‚ج‚إپA![]() ‚ًٹm‚©‚ك‚ـ‚·پB
‚ًٹm‚©‚ك‚ـ‚·پB
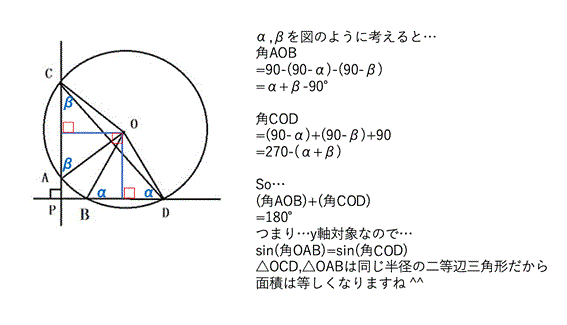
پœڈ‚µ‚¸‚آگ}‚ً•دŒ`‚µ‚ب‚ھ‚çچl‚¦‚ـ‚·پB
پEگ}1
‰~‚n‚ھچ¶‚ئ‰؛‚إ’¼گü‚ئگع‚µ‚ؤ‚¢‚é‚ئ‚µ‚ـ‚·پB
گع“_‚ً‚`پA‚a‚ئ‚·‚é‚ئپAپ¢‚n‚`‚a‚ح’¼ٹp“ٌ“™•سژOٹpŒ`‚إ‚·پB
پEگ}2
گ…•½‚ب’¼گü‚ًڈ‚µڈم‚ة‚¸‚炵‚ـ‚·پB
گ}‚ج‚و‚¤‚ة“_‚aپA‚cپA‚e‚ًŒˆ‚ك‚ـ‚·پB
‚·‚é‚ئ پ¢‚n‚`‚aپپپ¢‚n‚a‚c‚ئ‚ب‚è‚ـ‚·پB
‚ب‚؛‚ب‚çپA“_‚a‚©‚ç’¼گü‚n‚`‚ـ‚إ‚ج‹——£پA“_‚c‚©‚ç’¼گü‚n‚`‚ـ‚إ‚ج‹——£‚ھ“™‚µ‚‚ب‚é‚ج‚إپA
“ٌ‚آ‚جژOٹpŒ`‚ج’ê•س‚ئچ‚‚³‚ھ“™‚µ‚‚ب‚é‚©‚ç‚إ‚·پB
‚ـ‚½پAپع‚`‚n‚aپپپع‚c‚n‚e‚إ‚ ‚邱‚ئ‚à•ھ‚©‚è‚ـ‚·پB
‚ب‚؛‚ب‚çپAپ¢‚n‚a‚c‚ھ“ٌ“™•سژOٹpŒ`‚إ’¼گü‚`‚e‚ئ‚a‚c‚ھ•½چs‚¾‚©‚ç‚إ‚·پB
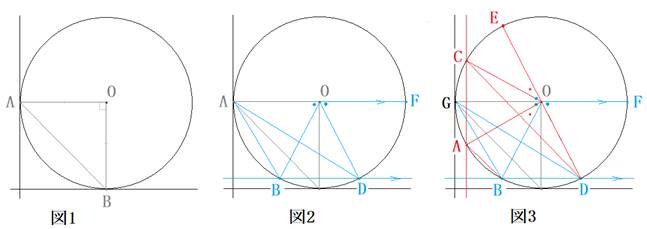
پEگ}3
ژں‚ةگ‚’¼‚ب’¼گü‚ً‰E‚ةڈ‚µ‚¸‚炵‚ـ‚·پB
گ}‚ج‚و‚¤‚ةپA“_‚`پA‚bپA‚dپA‚f‚ًŒˆ‚ك‚ـ‚·پB
پi‚d‚ح‚c‚n‚ج‰„’·ڈم‚إ‚·پB‚ـ‚½پA‚f‚حگ}1‚إ‚`‚¾‚ء‚½‚ئ‚±‚ë‚إ‚·پBپj
‚·‚é‚ئپAپع‚c‚n‚eپپپع‚d‚n‚f‚إ‚·پBپi‘خ’¸ٹpپj
‚و‚ء‚ؤپAپع‚a‚n‚fپپپع‚d‚n‚f‚إ‚·پBپiپع‚a‚n‚f‚حگ}2‚إپع‚`‚n‚a‚إ‚·پj
پ¢‚n‚`‚b‚ھ“ٌ“™•سژOٹpŒ`‚ب‚ج‚إپAپع‚`‚n‚fپپپع‚b‚n‚f‚إ‚·پB
‚و‚ء‚ؤپAپع‚`‚n‚aپپپع‚b‚n‚d‚إ‚·پB
ˆبڈم‚©‚çپAپ¢‚n‚`‚a‚ج’¸ٹpپع‚`‚n‚aپiپپپع‚b‚n‚dپj‚ئپ¢‚n‚b‚c‚ج’¸ٹpپع‚b‚n‚c‚جکa‚ھ180پ‹‚إ‚ ‚邱‚ئ‚ھ‚ي‚©‚è‚ـ‚·پB
NO5پuژOٹp’è‹Kپvپ@پ@پ@پ@02/04
13ژ22•ھ ژَگM چXگV 2/5
ٹٌ‚¹‚ç‚ꂽ–â‘è‚ج‰ً“ڑ‚إ‚·
ٹٌ‚¹‚ç‚ꂽ’ا‰ء–â‘è‚ج‰ً“ڑ‚إ‚·
<گ…‚ج—¬‚êپF2023”N‹“s‘هٹw‘Oٹْ“ْ’ِگ”ٹwپi—Œnپj‘و1–â‚ج–â2‚ج–â‘è‚ئ–â‚Pپi‚Uپj‚ج–â‘è‚ح‚ظ‚ع“¯‚¶‚إ‚µ‚½پB‚²——‚‚¾‚³‚¢پBپ„
’ا‰ء–â‘è‚Q‚ج‰ً–@
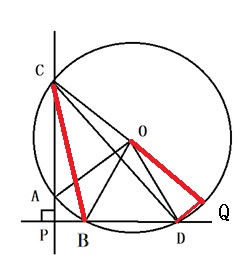
پ@گ}‚ج‚و‚¤‚ة, گü•ھ‚b‚a‚ئ, ‚p‚ً‚b‚n‚ج‰„’·‚ئ‰~‚جŒً“_‚ة‚ئ‚èپC‰~ژüٹpپع‚b‚p‚c‚ًچى‚éپB
‚ـ‚½, پع‚`‚n‚a=‚Qƒ؟, پع‚b‚n‚cپپ‚Qƒہ‚ئ‚·‚éپB
ژlٹpŒ`‚b‚a‚c‚p‚ح‰~‚ة“àگع‚·‚é‚©‚ç, پع‚b‚a‚cپ{پع‚b‚p‚cپپ‚P‚W‚Oپ‹پEپEپE‡@پ@
‰~ژüٹp‚ئ’†گSٹp‚جٹضŒW‚©‚ç, پع‚`‚b‚aپپƒ؟,پع‚b‚p‚cپپƒہ
‚ـ‚½,پع‚b‚a‚cپپƒ؟پ{‚X‚Oپ‹پiپ¢‚b‚o‚a‚جٹOٹp‚©‚çپj
‚و‚ء‚ؤ, ‡@‚ة‘م“ü‚µ‚ؤ, پiƒ؟پ{‚X‚Oپ‹پjپ{ƒہپپ‚P‚W‚Oپ‹
Œج‚ة, ‚Qƒ؟پ{‚Qƒہپپ‚P‚W‚Oپ‹
‚±‚±‚إ, ‰~‚n‚ج”¼Œa‚ً‚’‚ئ‚µ‚ؤ, ‘èˆس‚ج‚Q‚آ‚جژOٹpŒ`‚ج–تگد‚ً•\‚·‚ئ,
پ¢‚n‚`‚aپپپi1/2پj‚’‚Q‚“‚‰‚ژ‚Qƒ؟پ@پ@,پ@پ¢‚n‚b‚cپپپi1/2پj‚’‚Q‚“‚‰‚ژ‚Qƒہ
‚“‚‰‚ژ‚Qƒہپپ‚“‚‰‚ژپi‚P‚W‚Oپ‹پ\‚Qƒ؟پjپپ‚“‚‰‚ژ‚Qƒ؟‚©‚ç
پ@‘¦‚؟,پ@پ¢‚n‚`‚aپپپ¢‚n‚b‚cپ@پˆپ@ڈط–¾ڈI‚ي‚è
’ا‰ء–â‘è‚Q‚ج‰ً–@‚ج•ت‰ً
پuƒWƒ‡پ[ƒJپ[پv پ@03/07 پ@پ@
12ژ36•ھ ژَگM چXگV 3/7
ٹF‚³‚ٌپA–â‘è‚âژ؟–â‚ة“ڑ‚¦‚ؤ‚‚¾‚³‚¢پBˆê•”‚إ‚àچ\‚¢‚ـ‚¹‚ٌ‚©‚çپA‰ً“ڑ‚ئƒyƒ“ƒlپ[ƒ€‚ً“Y‚¦‚ؤپAƒپپ[ƒ‹‚إ‘—‚ء‚ؤ‚‚¾‚³‚¢پB‘ز‚ء‚ؤ‚¢‚ـ‚·پB
